- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Правильные многогранники
Содержание
- 1. Презентация по геометрии на тему Правильные многогранники
- 2. ПонятиеМногоугольник называется правильным, если у него равны
- 3. Какие они бывают?Правильных многогранников всего пять, и
- 4. ТетраэдрЧисло сторон у грани: 3 Число рёбер,
- 5. Гексаэдр или КубЧисло сторон у грани: 4
- 6. ОктаэдрЧисло сторон у грани: 3 Число рёбер,
- 7. ИкосаэдрЧисло сторон у грани: 3 Число рёбер,
- 8. ДодекаэдрЧисло сторон у грани: 5 Число рёбер,
- 9. Симметрия в правильных многогранникахПравильный тетраэдр не имеет
- 10. Пара интересных фактов…Правильные многогранники названы по имени
ПонятиеМногоугольник называется правильным, если у него равны стороны и углы. Примерно так же определяют правильные многогранники. «Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и двугранные углы при всех ребрах равны между
Слайд 2Понятие
Многоугольник называется правильным, если у него равны стороны и углы. Примерно
так же определяют правильные многогранники.
«Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и двугранные углы при всех ребрах равны между собой».
Существует и другое определение правильного многогранника:
«Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер».
Оба эти определения используются в математике как равноправные.
«Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и двугранные углы при всех ребрах равны между собой».
Существует и другое определение правильного многогранника:
«Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер».
Оба эти определения используются в математике как равноправные.
Слайд 3Какие они бывают?
Правильных многогранников всего пять, и два из них –
это тетраэдр и куб, который носит имя гексаэдр в ряду правильных многогранников. Каждый из такого рода многогранников имеет свое, отличное от других количество граней, поэтому и названия они когда-то получили благодаря этим числам: тетраэдр (4 грани, от греческого «тетра» - четыре и «хендрон» - основание, грань), гексаэдр (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней).
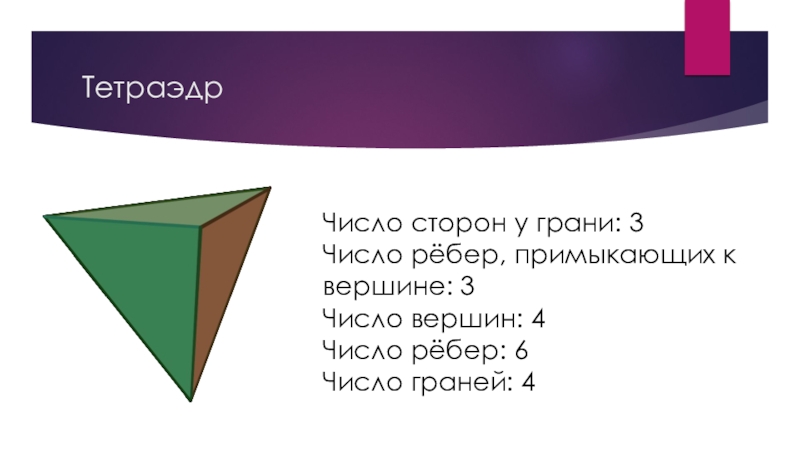
Слайд 4Тетраэдр
Число сторон у грани: 3
Число рёбер, примыкающих к вершине: 3
Число вершин:
4
Число рёбер: 6
Число граней: 4
Число рёбер: 6
Число граней: 4
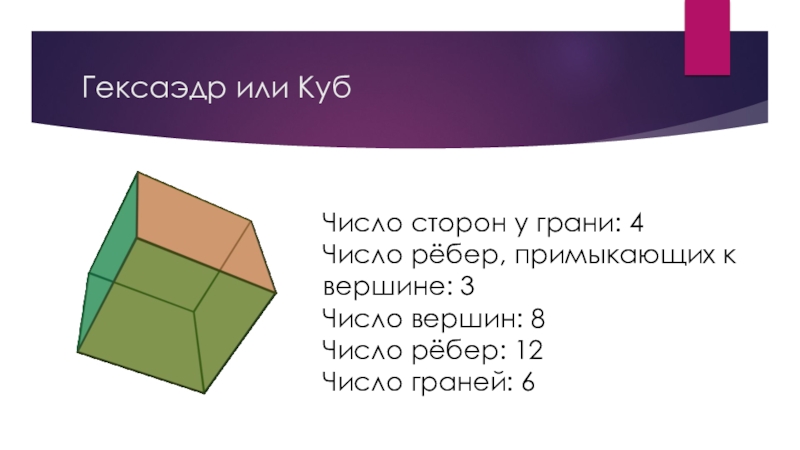
Слайд 5Гексаэдр или Куб
Число сторон у грани: 4
Число рёбер, примыкающих к вершине:
3
Число вершин: 8
Число рёбер: 12
Число граней: 6
Число вершин: 8
Число рёбер: 12
Число граней: 6
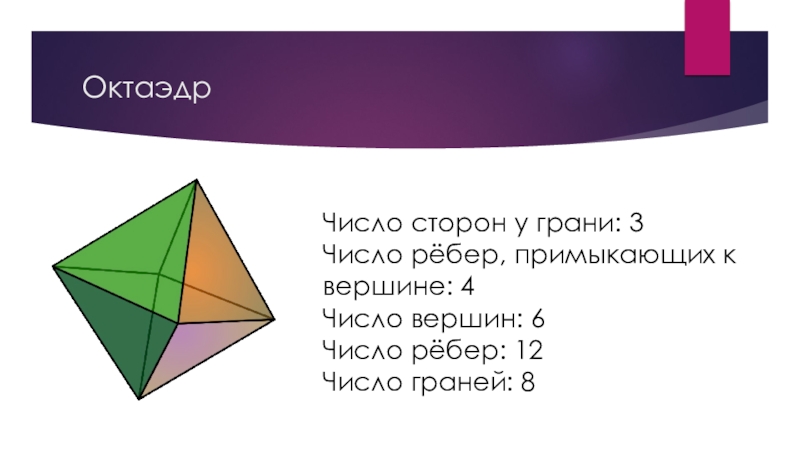
Слайд 6Октаэдр
Число сторон у грани: 3
Число рёбер, примыкающих к вершине: 4
Число вершин:
6
Число рёбер: 12
Число граней: 8
Число рёбер: 12
Число граней: 8
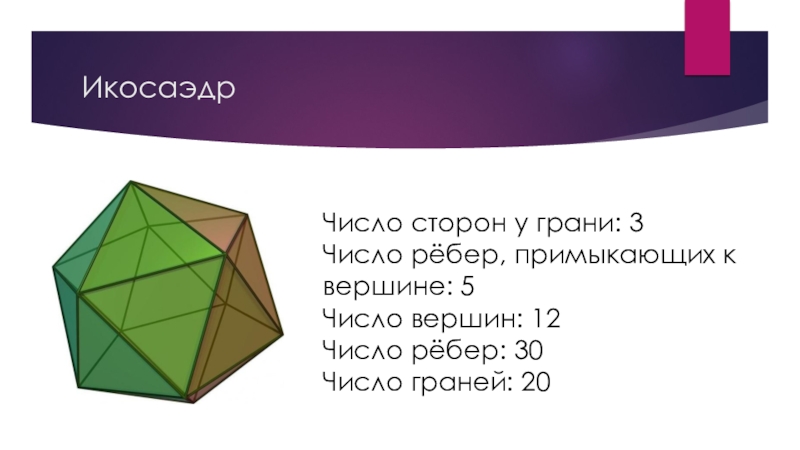
Слайд 7Икосаэдр
Число сторон у грани: 3
Число рёбер, примыкающих к вершине: 5
Число вершин:
12
Число рёбер: 30
Число граней: 20
Число рёбер: 30
Число граней: 20
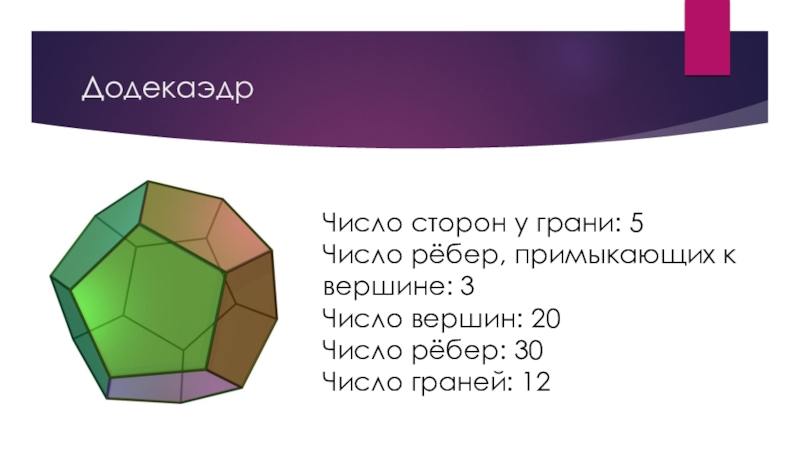
Слайд 8Додекаэдр
Число сторон у грани: 5
Число рёбер, примыкающих к вершине: 3
Число вершин:
20
Число рёбер: 30
Число граней: 12
Число рёбер: 30
Число граней: 12
Слайд 9Симметрия в правильных многогранниках
Правильный тетраэдр не имеет центра симметрии, но имеет
три оси симметрии и шесть плоскостей симметрии.
Куб имеет центр симметрии – точку пересечения его диагоналей. Ещё он имеет девять осей и девять плоскостей симметрии.
Октаэдр имеет центр симметрии, девять осей и столько же плоскостей симметрии.
Икосаэдр тоже имеет центр симметрии, пятнадцать осей и столько же плоскостей симметрии.
Додекаэдр – есть центр симметрии, есть пятнадцать осей и пятнадцать плоскостей симметрии.
Куб имеет центр симметрии – точку пересечения его диагоналей. Ещё он имеет девять осей и девять плоскостей симметрии.
Октаэдр имеет центр симметрии, девять осей и столько же плоскостей симметрии.
Икосаэдр тоже имеет центр симметрии, пятнадцать осей и столько же плоскостей симметрии.
Додекаэдр – есть центр симметрии, есть пятнадцать осей и пятнадцать плоскостей симметрии.
Слайд 10Пара интересных фактов…
Правильные многогранники названы по имени Платона – «Платоновы тела»
-, который в сочинении «Тимей» (IV век до н. э.) придавал им мистический смысл.
Иоганн Кеплер (великий учёный, астроном-оптик и первооткрыватель законов движения планет солнечной системы) пытался построить модель Солнечной системы, вписывая и описывая правильные многогранники в сферы. Это удалось ему не полностью, но послужило толчком к разработке Законов Кеплера.
Иоганн Кеплер (великий учёный, астроном-оптик и первооткрыватель законов движения планет солнечной системы) пытался построить модель Солнечной системы, вписывая и описывая правильные многогранники в сферы. Это удалось ему не полностью, но послужило толчком к разработке Законов Кеплера.