- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Показательные уравнения
Содержание
- 1. Презентация по алгебре на тему Показательные уравнения
- 2. Тема. Решение показательных уравнений. Цель : повторить
- 3. Повторение темы “показательная функция”. Решение показательных уравнений.Практическое
- 4. Повторение темы “показательная функция”.Функция, заданная формулой y
- 5. Свойства показательной функции1. Область определения – R
- 6. Новая тема.Показательными уравнениями называются уравнения, в которых
- 7. Решить уравнение: Пример 1Показательное уравнение af(x) = ag(x) равносильно уравнению f(x) = g(x).________________________________________________
- 8. Заданное уравнение равносильно уравнению______________________________________________Ответ: 2; 3.Проверка 1 примера
- 9. Пример 2Решить уравнение: Показательное уравнение af(x) = ag(x) равносильно уравнению f(x) = g(x)._____________________________________
- 10. Заданное уравнение равносильно уравнениюМожно записатьОтветПроверка 2 примера_______________________________________________
- 11. Пример 3Решить уравнениеПоказательное уравнение af(x) = ag(x) равносильно уравнению f(x) = g(x).__________________________________________
- 12. Заданное уравнение равносильно уравнениюпоэтому Ответ: 3; -1;Проверка 3 примера_____________________________________________
- 13. Пример 4Использование свойств степени, вынесение общего множителя за скобки_______________________________________________Решить уравнение
- 14. Использование свойств степени, вынесение общего множителя за скобкиПроверка 4 примера______________________________________________Ответ: 1.
- 15. Применение способа замены и приведения к квадратному уравнению___________________________________Пример 5Решить уравнение:
- 16. Сделаем замену переменной t = 2 x
- 17. Метод приведения к одинаковому показателюПример 6______________________________________________Решить уравнение:
- 18. Проверка 6 примера Это уравнение не является
- 19. Применение способа замены и приведения к квадратному уравнениюПример 7_________________________________________Решить уравнение:
- 20. данное уравнение равносильно уравнениюизбавляемся от знаменателя, получимдалее
- 21. Показательная функция находит важнейшие применения при изучении
- 22. Пример 1. Обозначим через m(t) массу колонии
- 23. Пример 2. В процессе радиоактивного распада вещества
- 24. Пример 3. Сумма вклада в сберегательном банке
- 25. Пример 4.Изучение возрастной структуры популяции рыб имеет
- 26. Авторы :учитель математики Сенина Галина Николаевнаучитель физики
Слайд 1Расскажи – и я забуду
Покажи – и
Дай мне сделать самому – и я научусь.
Китайская мудрость
Слайд 2Тема. Решение показательных уравнений.
Цель : повторить свойства показательных функций и
Психологическая установка учащимся:
Продолжаем отрабатывать навыки решения показательных уравнений. Продолжаем учиться решать. Формируем математическую интуицию, которая поможет ориентироваться в способах решения уравнений.
На уроке можно ошибаться, сомневаться, консультироваться.
Дать самому себе установку: “Понять и быть тем первым, который увидит ход решения”
Слайд 3
Повторение темы “показательная функция”.
Решение показательных уравнений.
Практическое применение показательной функции и
Ход урока
(выбирай раздел по порядку)
Слайд 4Повторение темы “показательная функция”.
Функция, заданная формулой y = ax (где а>0;
Свойства показательной функции
Слайд 5Свойства показательной функции
1. Область определения – R (множество действительных чисел).
2. область
3. При а > 1 функция возрастает на всей числовой прямой, при 0 < a < 1 функция убывает на всей числовой прямой.
4. .При любых действительных значениях X и Y справедливы равенства.
Слайд 6Новая тема.
Показательными уравнениями называются уравнения, в которых неизвестные содержатся в показателе
В основе решения показательных уравнений лежит следующая теорема:
Показательное уравнение af(x) = ag(x) равносильно уравнению f(x) = g(x).
Примеры 1Примеры 1,2Примеры 1,2,3Примеры 1,2,3,4Примеры 1,2,3,4,5Примеры 1,2,3,4,5,6Примеры 1,2,3,4,5,6,7
Слайд 7Решить уравнение:
Пример 1
Показательное уравнение af(x) = ag(x) равносильно
________________________________________________
Слайд 8Заданное уравнение равносильно уравнению
______________________________________________
Ответ: 2; 3.
Проверка 1 примера
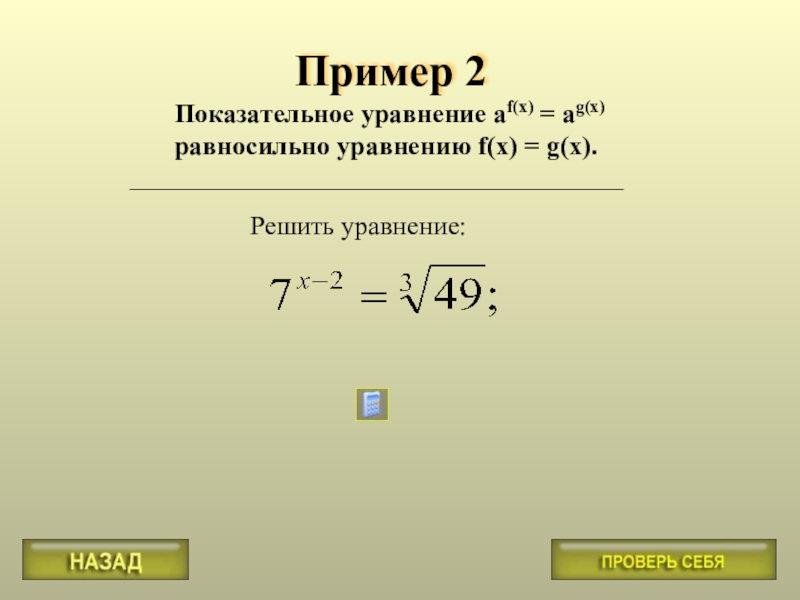
Слайд 9Пример 2
Решить уравнение:
Показательное уравнение af(x) = ag(x) равносильно
_____________________________________
Слайд 10Заданное уравнение равносильно уравнению
Можно записать
Ответ
Проверка 2 примера
_______________________________________________
Слайд 11Пример 3
Решить уравнение
Показательное уравнение af(x) = ag(x) равносильно уравнению
__________________________________________
Слайд 12Заданное уравнение равносильно уравнению
поэтому
Ответ: 3; -1;
Проверка 3 примера
_____________________________________________
Слайд 13Пример 4
Использование свойств степени, вынесение общего множителя за скобки
_______________________________________________
Решить уравнение
Слайд 14 Использование свойств степени, вынесение общего множителя за скобки
Проверка
______________________________________________
Ответ: 1.
Слайд 15Применение способа замены и приведения к квадратному уравнению
___________________________________
Пример 5
Решить уравнение:
Слайд 16Сделаем замену переменной t = 2 x . Заметим, что
Поэтому данное уравнение примет вид t 2– 5t + 4=0
По теореме Виета t1*t2=4
t1+t2=5, то t1=1; t2=4;
Решая уравнения вида
2х=1 и 2х=4
2х=20 2х=22
х = 0 х = 2
Ответ : 0 ; 2.
Проверка 5 примера
___________________________________________________
Слайд 17Метод приведения к одинаковому показателю
Пример 6
______________________________________________
Решить уравнение:
Слайд 18Проверка 6 примера
Это уравнение не является простейшим показательным уравнением, так
Но
можно записать в виде
получим х-3 = 0; х =3
Ответ : 3
________________________________________________________
Слайд 19Применение способа замены и приведения к квадратному уравнению
Пример 7
_________________________________________
Решить уравнение:
Слайд 20данное уравнение равносильно уравнению
избавляемся от знаменателя, получим
далее введем новую переменную 2x
уравнение 4t2-15t-4=0
D=225+64=289
t1=(15+17)/8=4
t2=(15-17)/8=-0,25
____________________________________________________
Проверка 7 примера
2x=4 2x= -0,25
2x=22 нет решения т.к. 2x>0
x=2
Ответ: 2
Слайд 21 Показательная функция находит важнейшие применения при изучении природных и общественных явлений.
Если обозначить через t0 (период полураспада) промежуток времени, необходимый для того, чтобы от первоначальной массы вещества m0 осталось половина её, то оставшаяся через t лет масса выразится так:
т.е. радиоактивный распад совершается по закону, выражаемому показательной функцией.
Степенные зависимости более высокого порядка также встречаются на практике. Например, по закону Стефана – Больцмана излучательная способность абсолютно чёрного тела пропорциональна четвёртой степени его температуры. Масса шара является кубической функцией его радиуса.
В естествознании и технике встречаются процессы, рост или затухание которых происходит быстрее, чем у любой степенной функции. С примерами быстро растущих функций человек столкнулся очень давно. В древней легенде об изобретателе шахмат говорится, что он потребовал за первую клетку шахматной доски одно пшеничное зерно, а за каждую следующую – вдвое больше, чем за предыдущую.
Необходимость изучения функций, у которых производная пропорциональна самой функции, возникла с обнаружением различных законов естествознания, таких, как законы размножения, законы радиоактивного излучения, законы движения в тормозящей среде т. д.
Практическое применение показательной функции и показательных уравнений
Примеры 1Примеры 1, 2Примеры 1, 2, 3Примеры 1, 2, 3,4
Слайд 22Пример 1. Обозначим через m(t) массу колонии бактерий в момент времени
Аналогично обстоят дела для любой совокупности живых существ при условии, что нет ограни пище и пространстве и нет истребляющих их врагов. Поэтому процессы, в которых величина увеличивается за равные промежутки времени в одно и то же число раз, называют процессами органического роста.
Слайд 23Пример 2. В процессе радиоактивного распада вещества его масса m(t) за
Слайд 24Пример 3. Сумма вклада в сберегательном банке за данный промежуток времени
Слайд 25Пример 4.
Изучение возрастной структуры популяции рыб имеет большое значение для рыболовного
Популяция рассматривается как “открытая термодинамическая система, находящаяся в состоянии непрерывного обмена с окружающей средой, самовоспроизводящаяся и саморегулирующаяся.
Предполагается исходить из принципа стационарного состояния открытых систем, согласно которому все живые системы стремятся сохранить свою структуру (и энтропию) неизменной во времени.
Формула расчета численности выглядит как
Зная по результатам экспериментального лова массу mi особи i-го возраста, а также число особей Ni, можно найти общую численность популяции N и остальные численности Nj, общую массу популяции. Были проведены расчеты для сельди Северного моря с 1947 по 1971 год. Сравнение расчетных и реальных значений дало совпадение от 70% и выше за каждый год, кроме одного.
Слайд 26Авторы :
учитель математики Сенина Галина Николаевна
учитель физики Сенин Валентин Георгиевич
ученик 11
Что быстрее всего ? – Ум.
Что мудрее всего ? – Время.
Что приятнее всего ? – Достичь желаемого.
Фалес.
До свидания