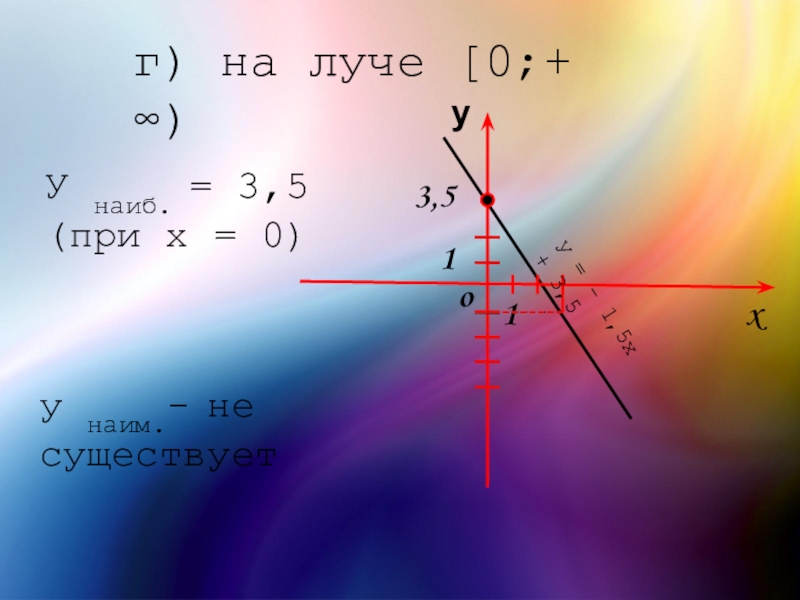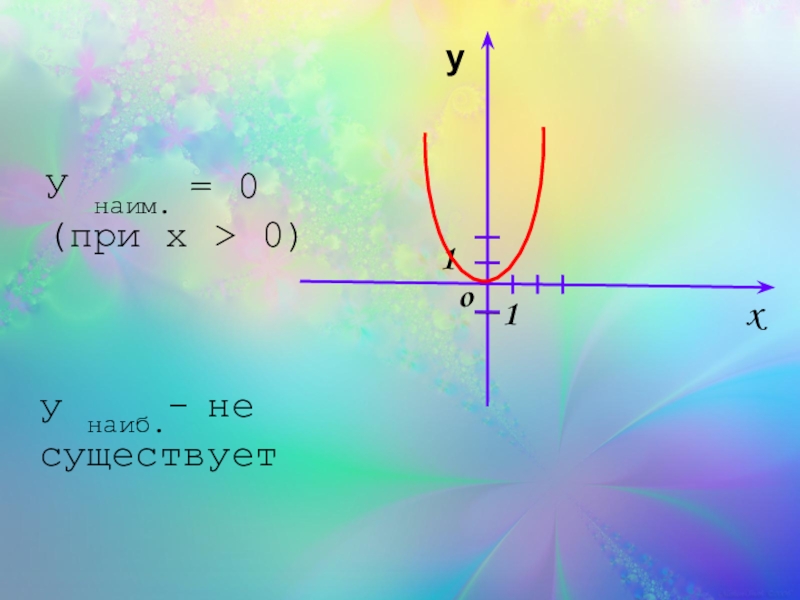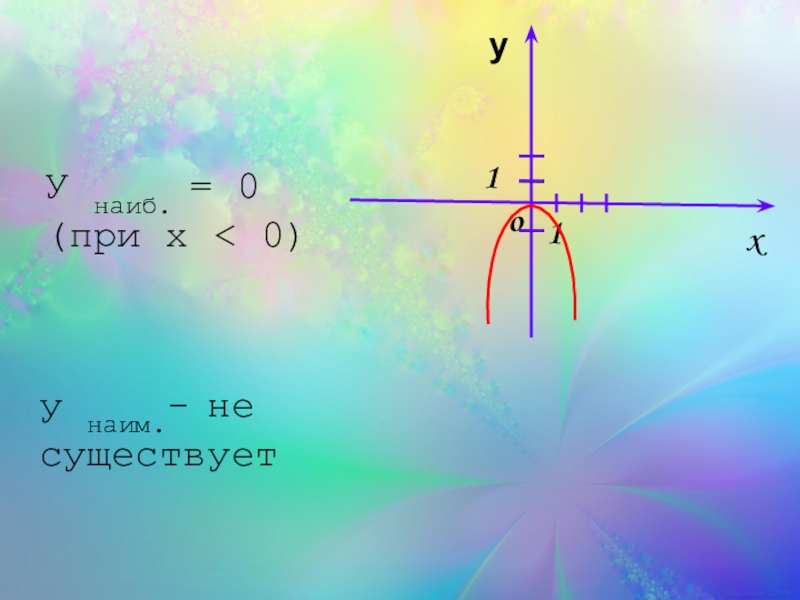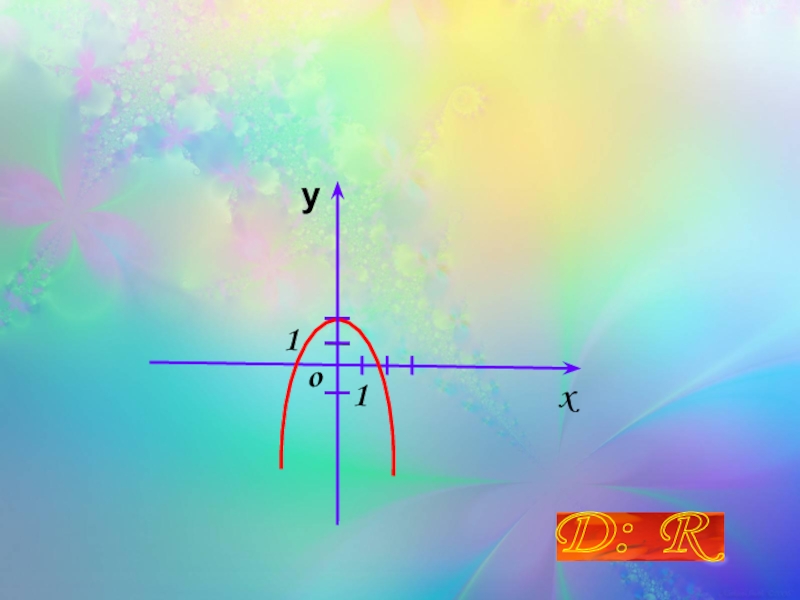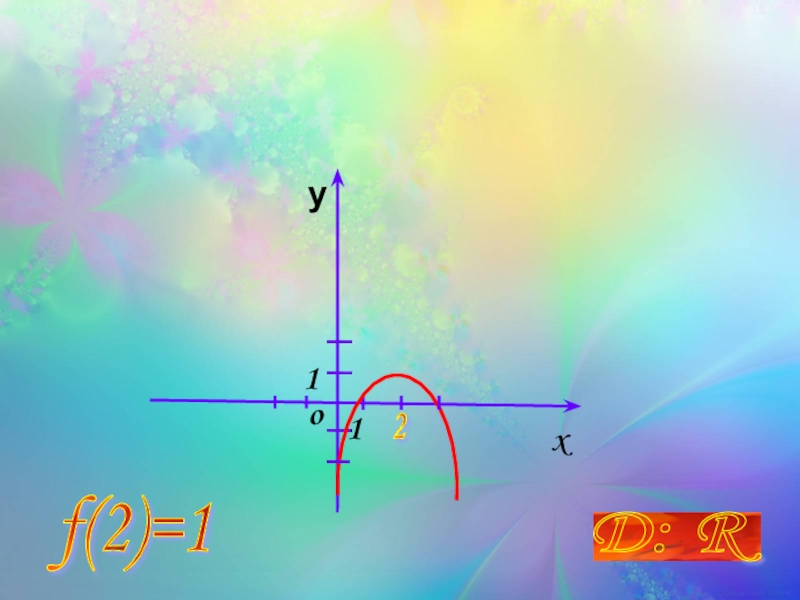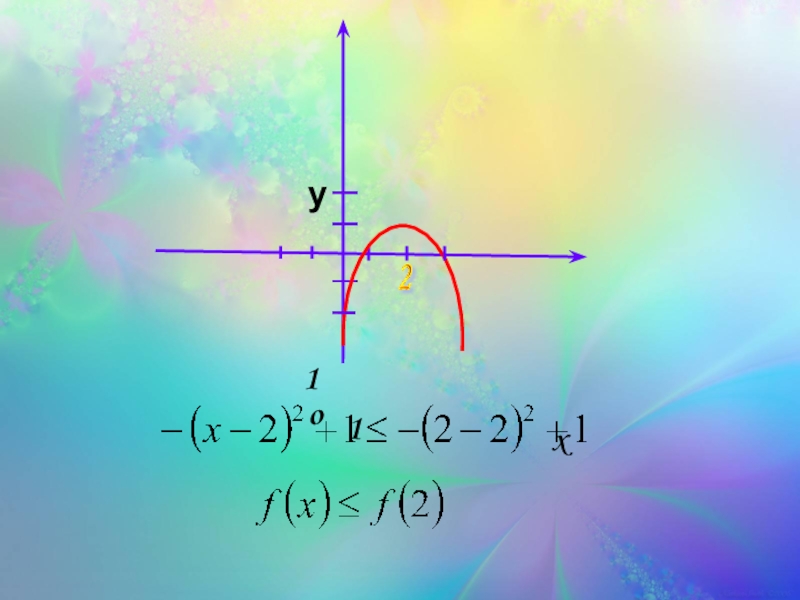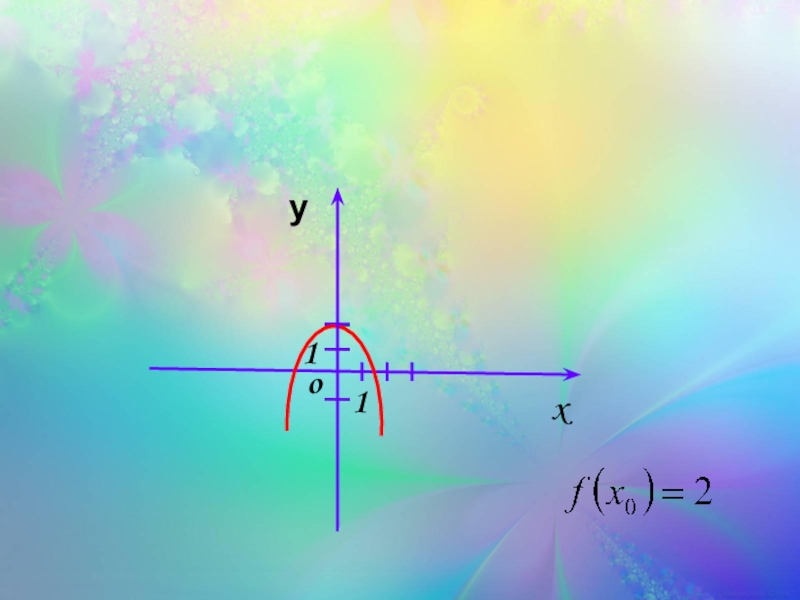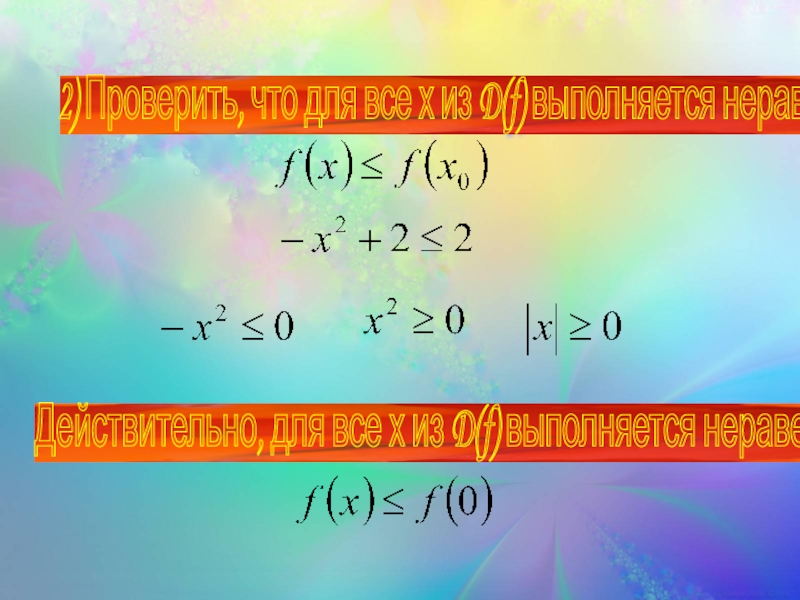- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Наибольшее и наименьшее значение функции
Содержание
- 1. Презентация по алгебре на тему Наибольшее и наименьшее значение функции
- 2. Последние 6 месяцев Владимир Петрович,
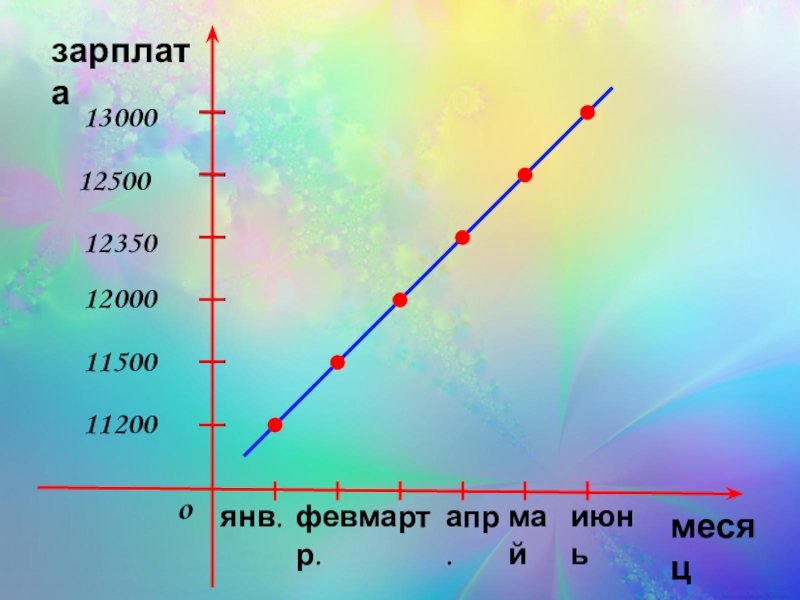
- 3. Изобразите график соотношения месяца и зарплаты
- 4. месяцo февр. янв. 11200 зарплата март апр. май июнь 11500 12000 12350 12500 13000
- 5. Укажите месяц , в который была самая большая и самая маленькая зарплата.
- 6. Зарплата ( апрель) = 11200 –
- 7. Для дальнейшего изучения функции, для
- 8. Рассмотрим самое маленькое и самое большое значение линейной функции
- 9. Найти наибольшее и наименьшее Значения линейной
- 10. Составим таблицу для линейной функции у = x / 4 + 4.уx0476
- 11. Построим на координатной плоскости xOy точки
- 12. Рассмотрим эту линейную функцию не целиком
- 13. Самая большая ордината у точек
- 14. Самая маленькая ордината у
- 15. Найти у наиб. и у наим. для
- 16. Составим таблицу для линейной функции у = - 1,5x + 3,5уx12- 45
- 17. Построим на координатной плоскости xOy точки
- 18. a)на отрезке [1;5] у xo 5 1
- 19. б) на интервале (1;5) xo 5
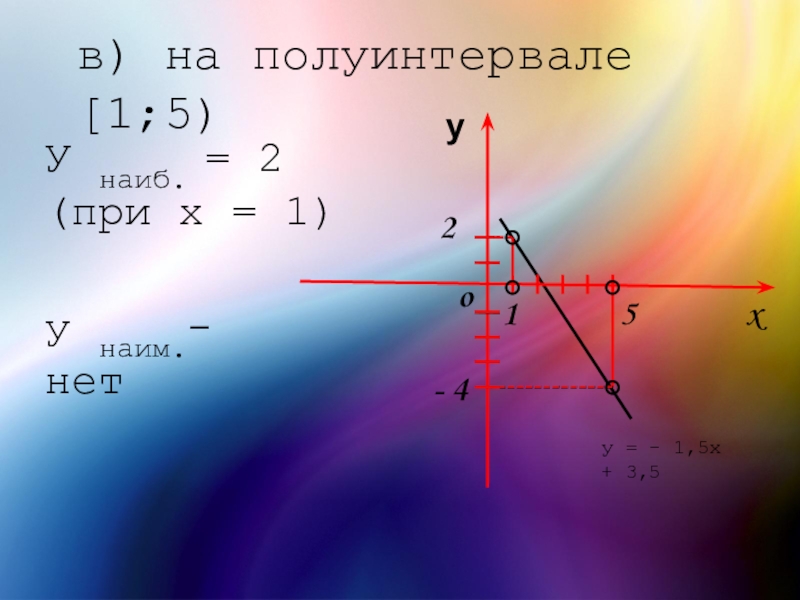
- 20. в) на полуинтервале [1;5)xo 5 1 -
- 21. г) на луче [0;+ ∞)xo 1 3,5
- 22. Вывод:Мы научились находить наибольшее и наименьшее
- 23. Найти наибольшее и наименьшее значения функции
- 24. xo 1 1 у У наим. = 0 (при x > 0)у наиб.- не существует
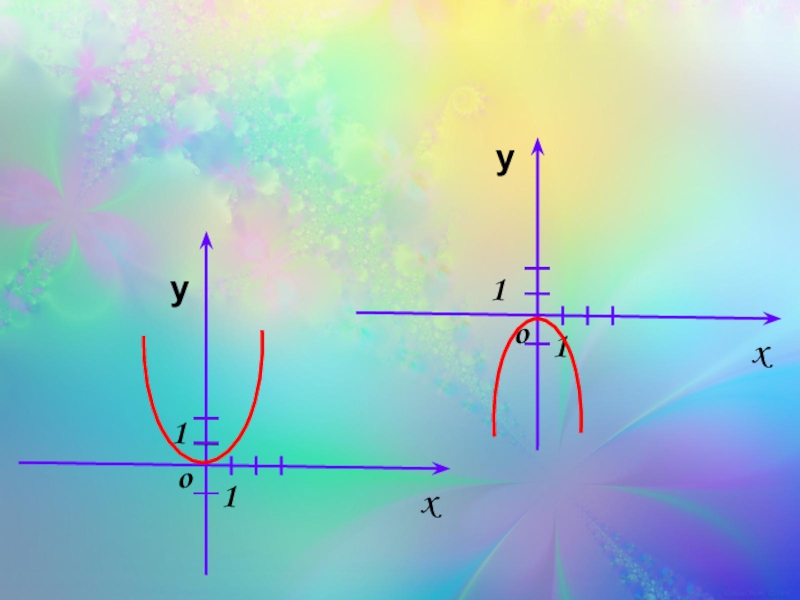
- 25. Найти наибольшее и наименьшее значения функции
- 26. xo 1 1 у У наиб. = 0 (при x < 0)у наим.- не существует
- 27. xo 1 1 у xo 1 1 у Какой можно вывод сделать?
- 28. Если ветви параболы направлены вниз, то
- 29. Если ветви параболы направлены вниз, то
- 30. xo 1 1 у Найти область определения функции y= - x 2+2 D: R
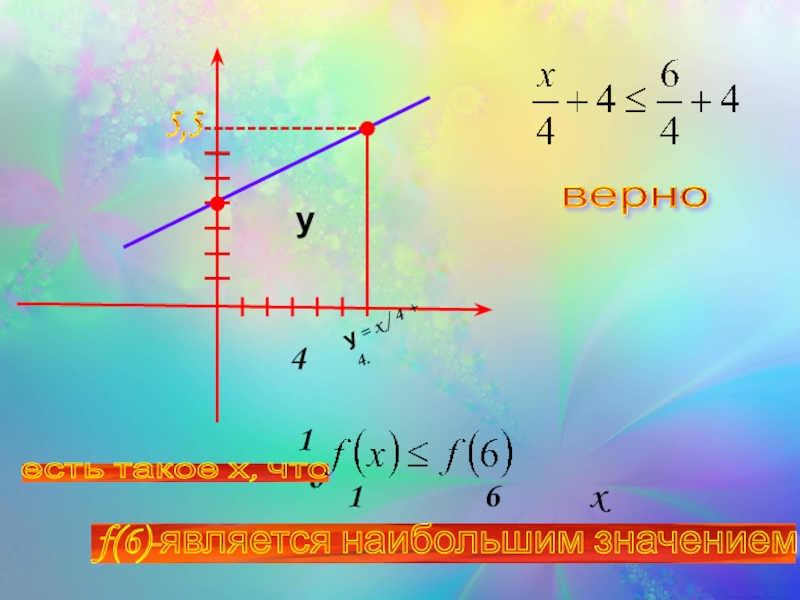
- 31. у xo 6 1 1 4 у
- 32. у xo 6 1 1 4 у
- 33. xo 5 1 - 4 2 у
- 34. xo 1 1 у Найти область определения
- 35. xo 1 1 у 2
- 36. Что означает,что наибольшее значение равно 1? Все
- 37. Запишем в следующем виде: для всех х из Х выполняется f(x) ≤ f(x 0 )
- 38. Для наименьшего значения функции для всех х из Х выполняется f(x) ≥ f(x 0 )
- 39. Сформулируем определение наибольшего и наименьшего значения функции
- 40. Число m называют наименьшим значением функции y
- 41. Число М называют наибольшим значением функции y
- 42. xo 1 1 у Какое число является наибольшим значением функции y= - x 2+2 ?
- 43. 1) Проверить существование точки
- 44. Проверим выполнимость алгоритма: В D(f) существует точка
- 45. 2) Проверить, что для все х из
- 46. Так как точка х была взята
Слайд 2 Последние 6 месяцев Владимир Петрович, работая на заводе , получал
Слайд 7Для дальнейшего изучения функции, для нас важно рассмотрение самого
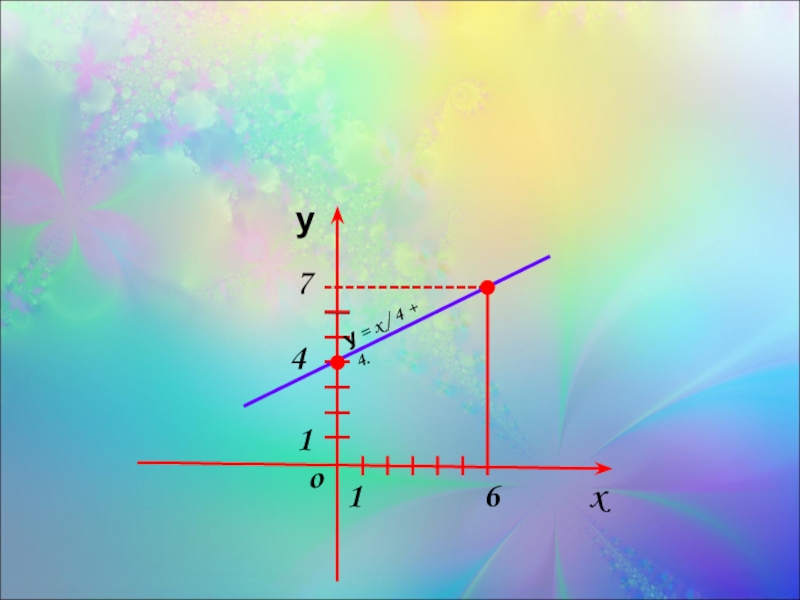
Слайд 11Построим на координатной плоскости xOy точки (0; 4) и (6;7) и
у
x
o
6
1
1
4
7
у = x / 4 + 4.
Слайд 13Самая большая ордината у точек , принадлежащих выделенной части прямой
Слайд 14Самая маленькая ордината у точек , принадлежащих выделенной части
Слайд 15Найти у наиб. и у наим. для линейной функции у =
a)на отрезке [1;5]
б) на интервале (1;5)
в) на полуинтервале [1;5)
г) на луче [0;+ ∞)
Слайд 17Построим на координатной плоскости xOy точки (1; 2) и (5;-4) и
у
x
o
5
1
- 4
2
у = - 1,5x + 3,5
Слайд 18a)на отрезке [1;5]
у
x
o
5
1
- 4
2
У
у наим. = -4
(при x = 5)
у = - 1,5x + 3,5
Слайд 19б) на интервале (1;5)
x
o
5
1
- 4
2
Ни наибольшего,
ни наименьшего значений на заданном интервале у линейной функции
у = - 1,5x + 3,5 нет.
у = - 1,5x + 3,5
у
Слайд 21г) на луче [0;+ ∞)
x
o
1
3,5
у = - 1,5x
1
У наиб. = 3,5
(при x = 0)
у наим.- не существует
у
Слайд 22Вывод:
Мы научились находить наибольшее
и наименьшее значение линейной функции.
Выяснили ,что наибольшее
Наибольшее и наименьшее значение линейной функции
достигается на концах отрезка.
Слайд 28Если ветви параболы направлены вниз,
то функция имеет наибольшее значение.
Если ветви
Слайд 29Если ветви параболы направлены вниз, то функция ограничена сверху, т.е.все значения
Если ветви параболы направлены вверх,
то функция ограничена снизу, т.е. все значения
функции больше некоторого числа.
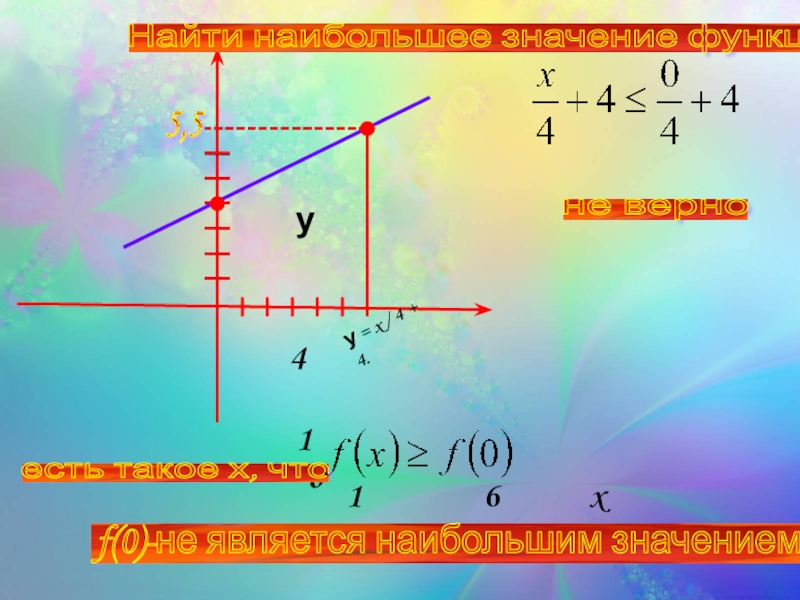
Слайд 31у
x
o
6
1
1
4
у = x / 4
не верно
есть такое х, что
f(0)-не является наибольшим значением
5,5
Найти наибольшее значение функции
Слайд 33x
o
5
1
- 4
2
у = - 1,5x +
у
Найти наибольшее значение функции
Не существует
такое что
следовательно нет
наибольшего значения функции
Слайд 34x
o
1
1
у
Найти область определения и
наибольшее
D: R
2
f(2)=1
Слайд 36Что означает,что наибольшее значение равно 1?
Все остальные значения функции меньше
Для всей ли области определения это выполняется?
Да, для всех
, где X область определения функции
Слайд 40Число m называют наименьшим значением функции y = f (x) на множестве
1) в Х существует
такая точка x 0, что f (x 0 ) = m
2) для всех х из Х выполняется неравенство
f(x) ≥ f(x 0 )
Слайд 41Число М называют наибольшим значением функции y = f(x) на множестве X
1) в Х существует
такая точка x 0, что f (x 0 ) = М
2) для всех х из Х выполняется неравенство
f(x) ≤ f(x 0 )
Слайд 431) Проверить существование точки из D(f), такой что
Доказать, что -
наибольшее значение функции
Чтобы доказать, что -
наибольшее значение функции нужно:
2) Проверить, что для все х из D(f) выполняется неравенство
Слайд 44Проверим выполнимость алгоритма:
В D(f) существует точка
1) Проверить существование точки из D(f), такой что
Слайд 452) Проверить, что для все х из D(f) выполняется неравенство
Действительно, для
Слайд 46Так как точка х была взята произвольно, а для неё выполняет
а значит выполнены все существенные признаки
в определении наибольшего значения функции,
поэтому М=2 -
наибольшее значение функции








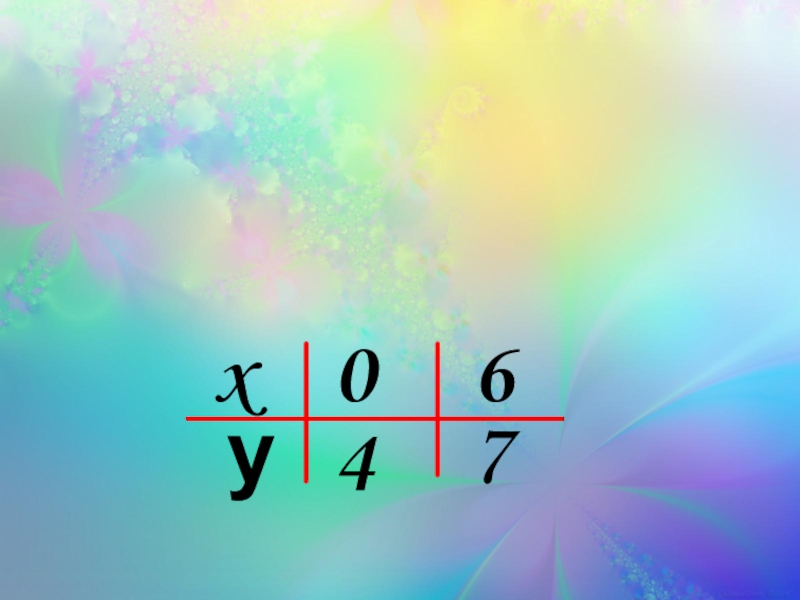
![Презентация по алгебре на тему Наибольшее и наименьшее значение функции Рассмотрим эту линейную функцию не целиком , а на отрезке [0:6], Рассмотрим эту линейную функцию не целиком , а на отрезке [0:6], т.е для x є](/img/tmb/5/493336/409183deb0d594d2165ff19efef4fbb6-800x.jpg)




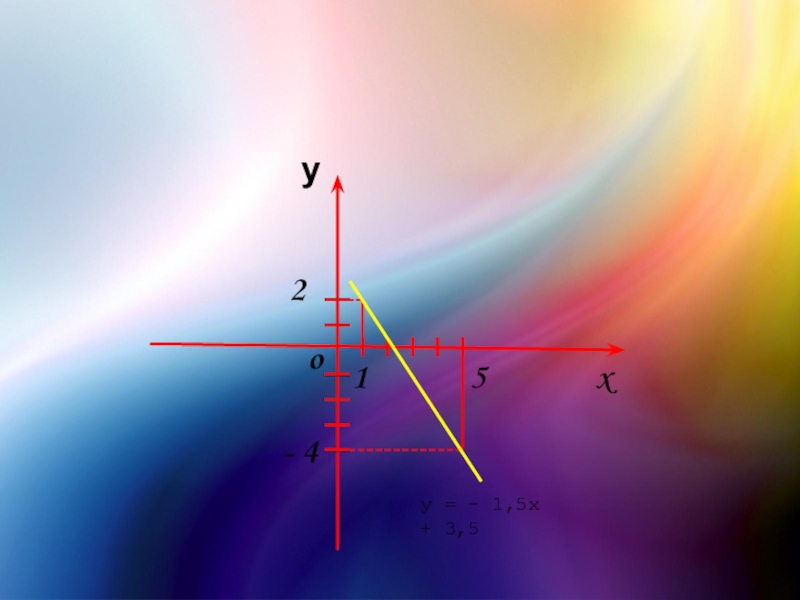
![Презентация по алгебре на тему Наибольшее и наименьшее значение функции a)на отрезке [1;5] у xo 5 1 - 4 2 У a)на отрезке [1;5] у xo 5 1 - 4 2 У наиб. = 2 (при x =](/img/tmb/5/493336/cb2b03239ed1fa5267c43df92f629cc1-800x.jpg)