- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Матрица. Определитель 2-3го порядка
Содержание
- 1. Презентация по алгебре Матрица. Определитель 2-3го порядка
- 2. Что такое матрица? Матрицей A = Amn
- 3. Чего НЕЛЬЗЯ делатьПереставлять элементы матрицыСкладывать элементы матрицы
- 4. Сложение матрицНе все матрицы можно складывать!Они должны
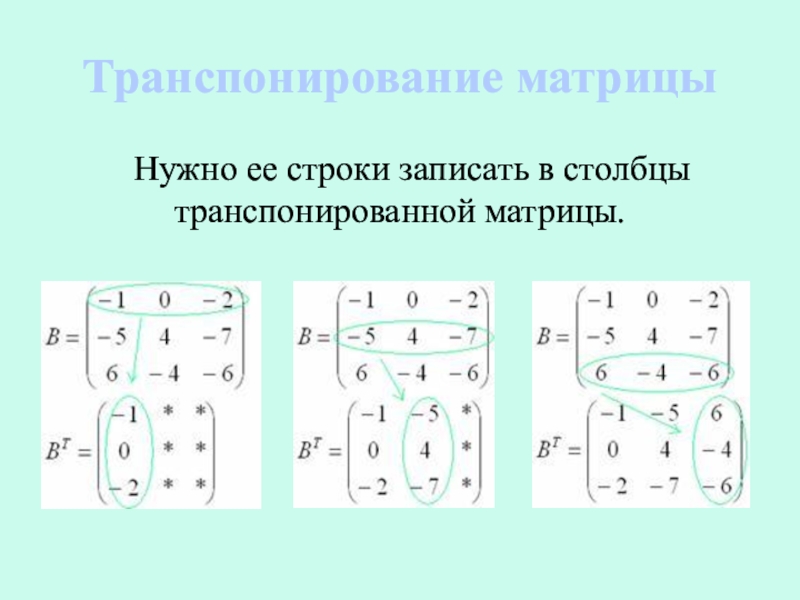
- 5. Транспонирование матрицыНужно ее строки записать в столбцы транспонированной матрицы.
- 6. Внесение (вынесение) минусаЧтобы вынести минус, нужно сменить знак у каждого элемента матрицы.
- 7. Умножение матрицы на числоНужно умножить на число каждый элемент матрицы.
- 8. Слайд 8
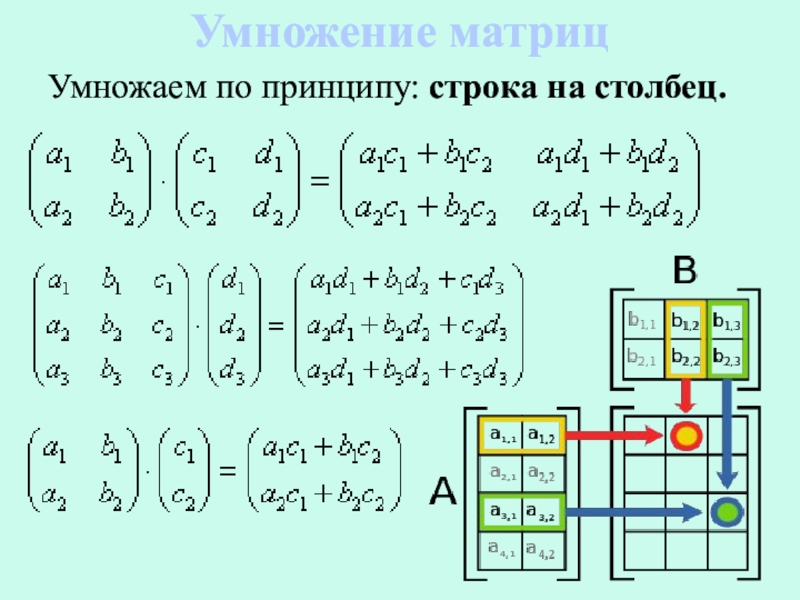
- 9. Умножение матрицУмножаем по принципу: строка на столбец.
- 10. Возведение в степень. Актуально только для квадратных
- 11. Определитель. Определи́тель (или детермина́нт) — это многочлен,
- 12. Определитель первого порядкаДля матрицы первого порядка значение
- 13. Определитель второго порядка. Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:
- 14. Определитель третьего порядка можно считать разными способами. The choice is yours.
- 15. Определитель 3-го порядка. Способ Саррюса (параллельных полосок)Справа
- 16. Определитель 3-го порядка. Способ Саррюса (параллельных полосок)
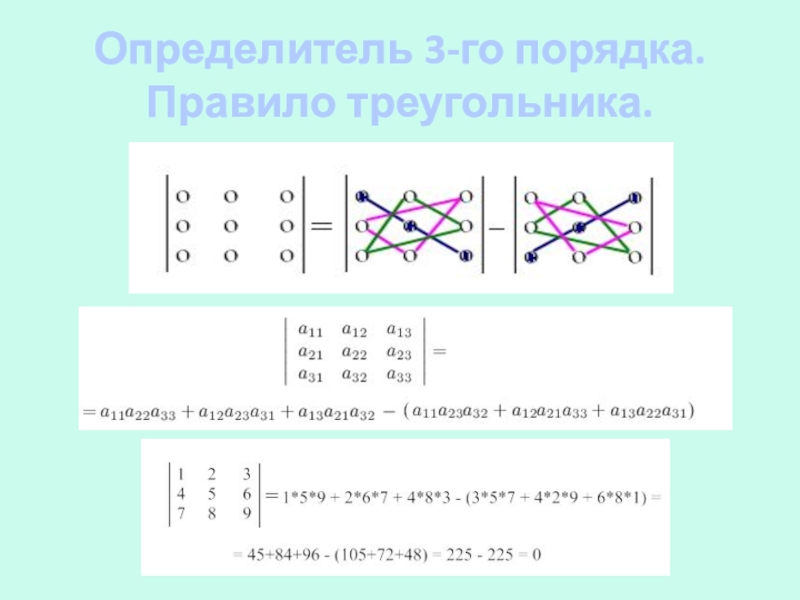
- 17. Определитель 3-го порядка. Правило треугольника.
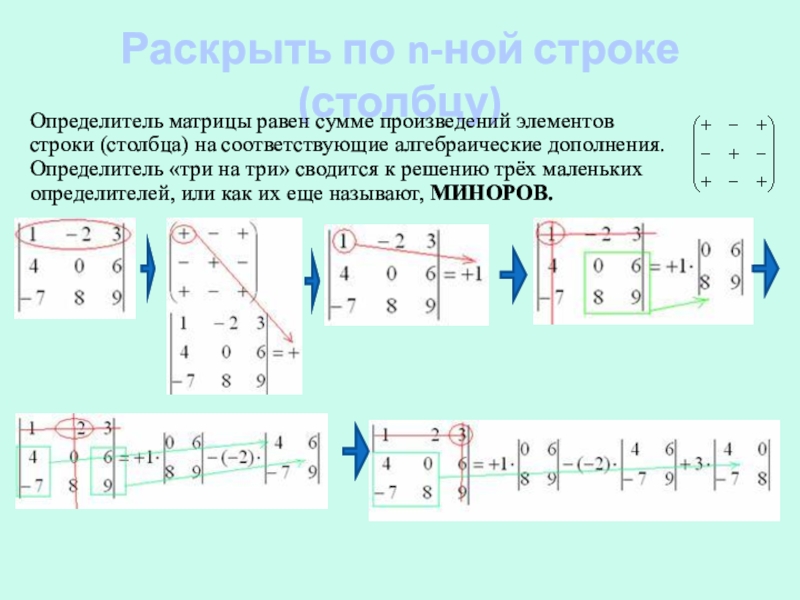
- 18. Раскрыть по n-ной строке (столбцу)Определитель матрицы равен
- 19. Ступенчатый определительОсобый случай, когда определитель имеет так
- 20. Свойства определителя1. Если все элементы строки или
- 21. Свойства определителя4. Определитель равен нулю, если элементы
- 22. Свойства определителя 6. Общий сомножитель строки (столбца) может
- 23. Свойства определителя7. Определитель не изменится, если к
- 24. Стоп! Так я могу не считать сразу всё?
- 25. Понижение порядка определителя Получим ноль слева вверху:Для
- 26. Идея: получить 2 нуля в какой-то строке или столбце, тем самым понизив порядок определителя.
Что такое матрица? Матрицей A = Amn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.Матрица «два на три» (две строки, три столбца) Матрица «три на три» – квадратная Матрицы с
Слайд 2Что такое матрица?
Матрицей A = Amn порядка m*n называется прямоугольная
таблица чисел, содержащая m - строк и n - столбцов.
Матрица «два на три» (две строки, три столбца)
Матрица «три на три» – квадратная
Матрицы с только одним столбцом или только одной строкой называют векторами.
Слайд 4Сложение матриц
Не все матрицы можно складывать!
Они должны быть одинаковы по размеру.
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы.
Слайд 6Внесение (вынесение) минуса
Чтобы вынести минус, нужно сменить знак у каждого элемента
матрицы.
Слайд 8
, значит, умножать
нельзя
нельзя
m = n, значит, умножать
можно
Умножение матриц
Порядок важен!
Чтобы матрицу K можно было умножить на матрицу L нужно, чтобы число столбцов матрицы K равнялось числу строк матрицы L .
Слайд 10Возведение в степень.
Актуально только для квадратных матриц.
m>1 - целое
положительное число. А - квадратная матрица.
Слайд 11Определитель.
Определи́тель (или детермина́нт) — это многочлен, комбинирующий элементы квадратной матрицы
таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов.
Обозначается det(A), |А| или Δ(A).
Порядок определителя равен числу столбцов и числу строк матрицы.
Вычислить определитель – это значит НАЙТИ ЧИСЛО.
Обозначается det(A), |А| или Δ(A).
Порядок определителя равен числу столбцов и числу строк матрицы.
Вычислить определитель – это значит НАЙТИ ЧИСЛО.
Слайд 12Определитель первого порядка
Для матрицы первого порядка значение определителя равно значению элемента
этой матрицы:
∆ = |a11| = a11
|3| = 3
∆ = |a11| = a11
|3| = 3
Слайд 13Определитель второго порядка.
Для матрицы 2×2 значение определителя равно разности произведений
элементов главной и побочной диагоналей:
Слайд 15Определитель 3-го порядка. Способ Саррюса (параллельных полосок)
Справа от определителя дописывают первых
два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус».
Слайд 18Раскрыть по n-ной строке (столбцу)
Определитель матрицы равен сумме произведений элементов строки
(столбца) на соответствующие алгебраические дополнения. Определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ.
Слайд 19Ступенчатый определитель
Особый случай, когда определитель имеет так называемый ступенчатый или треугольный
вид, например:
– в таком определителе все числа, расположенные ниже главной диагонали, равны нулю.
Ступенчатый определитель равен произведению чисел его главной диагонали:
– в таком определителе все числа, расположенные ниже главной диагонали, равны нулю.
Ступенчатый определитель равен произведению чисел его главной диагонали:
Слайд 20Свойства определителя
1. Если все элементы строки или столбца равны нулю, то
и определитель равен нулю.
2. Определитель изменит знак, если поменять местами какие-либо 2 строки или столбца.
2. Определитель изменит знак, если поменять местами какие-либо 2 строки или столбца.
3. Определитель транспонированной матрицы равен определителю исходной матрицы.
Слайд 21Свойства определителя
4. Определитель равен нулю, если элементы одной строки пропорциональны (или
равны) соответствующим элементам другой строки (для столбцов также).
Слайд 22Свойства определителя
6. Общий сомножитель строки (столбца) может быть вынесен за знак
определителя. (НЕ общий множитель ВСЕХ элементов!)
Слайд 23Свойства определителя
7. Определитель не изменится, если к элементам какой-либо строки (столбца)
прибавить соответствующие элементы другой строки (столбца), умноженные на одну и ту же величину.
Слайд 25Понижение порядка определителя
Получим ноль слева вверху:
Для этого вторую строку умножим
на 3: (–3, 6) и к первой строке прибавим вторую строку, умноженную на 3:
Слайд 26Идея: получить 2 нуля в какой-то строке или столбце, тем самым
понизив порядок определителя.
