Математика владеет не только истиной, но и высшей красотой.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад открытого мероприятия Красота математики
Содержание
- 1. Презентация открытого мероприятия Красота математики
- 2. Математика –
- 3. Люди придумали цифры и действия с ними,
- 4. 1 x 8 + 1 = 9
- 5. 1x 9 + 2 = 11
- 6. 9 x 9 + 7 = 88
- 7. 1 x 1 = 1 11 x
- 8. Возьмем число 142857. Удвоим его. Получилось 285714.Внимательно
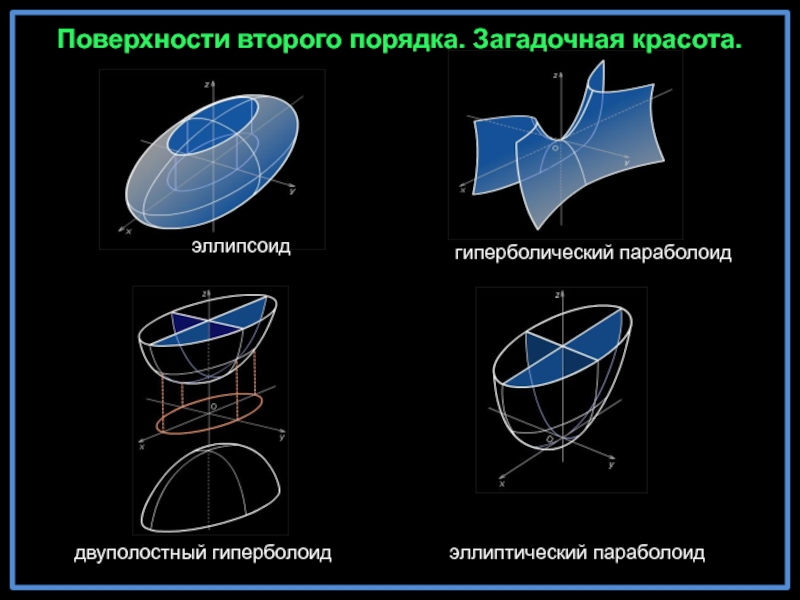
- 9. Поверхности второго порядка. Загадочная красота.эллипсоидгиперболический параболоидэллиптический параболоиддвуполостный гиперболоид
- 10. «...быть прекрасным значит быть симметричным и соразмерным»
- 11. Тадж-Махал — мавзолей-мечеть, находящийся в Агре, Индия,
- 12. Особенно блистательно использовали симметрию в архитектурных сооружениях
- 13. Зеркальная симметрия Если преобразование симметрии
- 14. Симметрия в природе Симметрия широко распространена в
- 15. Рассматривая расположение листьев на ветке дерева, видим,
- 16. В мир неживой природы очарование симметрии вносят
- 17. О, симметрия! Гимн тебе пою! Тебя повсюду
- 18. В 1968г. Венгерский биолог и ботаник Аристид
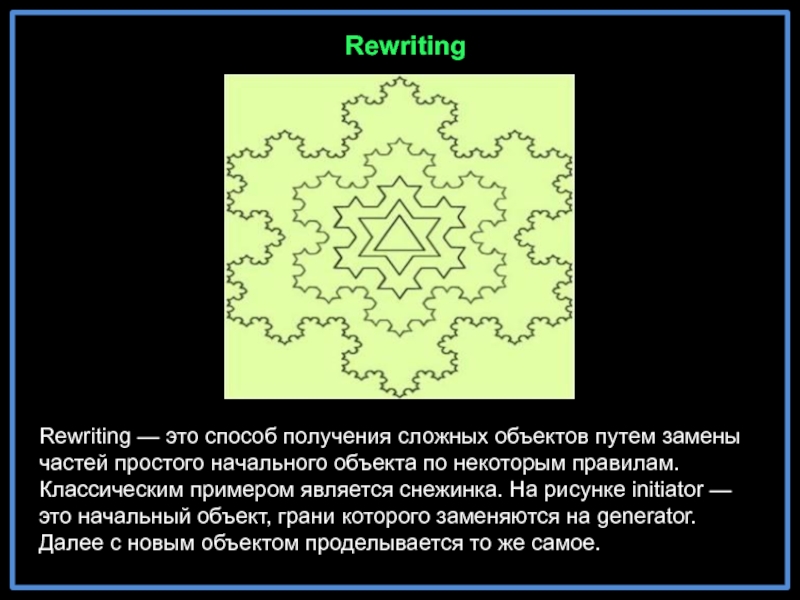
- 19. Rewriting — это способ получения сложных объектов
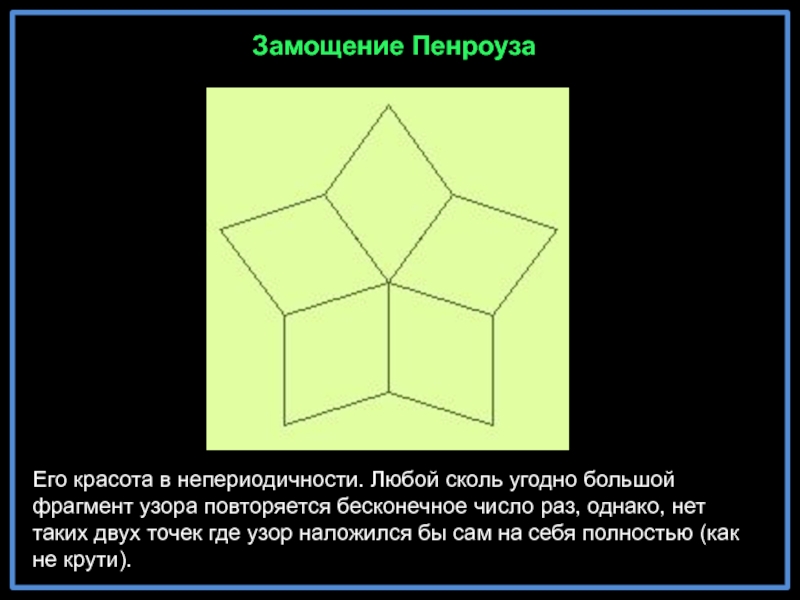
- 20. Его красота в непериодичности. Любой сколь угодно
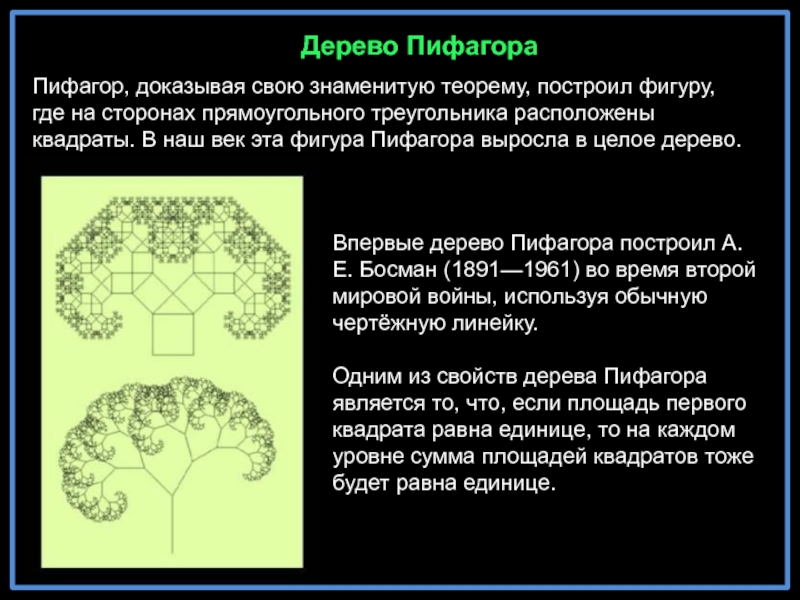
- 21. Пифагор, доказывая свою знаменитую теорему, построил фигуру,
- 22. Обнаженное дерево ПифагораКлассическое дерево ПифагораЕсли изображать только
- 23. Обдуваемое ветром дерево ПифагораЕсли в классическом дереве
- 24. Гипножаба
- 25. Первые примеры самоподобных множеств с необычными свойствами
- 26. Они кажутся более живыми и красивыми, чем
- 27. Пифагор создал свою школу мудрости, положив в
- 28. Эта последовательность имеет следующий вид: 1,1,2,3,5,8,13,21,... То
- 29. Золотое сечение (золотая пропорция, деление в крайнем
- 30. Пирамида Хеопса, Египет
- 31. Еще Гете подчеркивал тенденцию природы к спиральности.
- 32. В биологических исследованиях 70-90 гг. показано, что,
- 33. Золотое сечение в живописи
- 34. Закономерности золотой симметрии проявляются в энергетических переходах
- 35. В математике есть тоже своя красота, как
- 36. Использованные ресурсы:http://mcs.open.ac.uk/ugg2/jpg/med_RS_0065.jpghttp://en.wikipedia.org/wiki/Penrose_tilinghttp://habrahabr.ru/blogs/biotech/69989http://ru.wikipedia.org/wiki/http://ru.wikipedia.org/wiki/Фракталhttp://fractals.narod.ru/intro.htmhttp://www.wack.ch/frac/gallery.htmlhttp://www.ug.ru/issue/?action=topic&toid=8652http://www.mathematics.ru/«Математика и искусство», А. В. Волошинов,
Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства. Это не только стройная система законов, но и уникальное
Слайд 1
М
А
Т
Е
А
М
Т
И
К
А
В математике есть своя красота, как в живописи и поэзии.
(Н.Е.
Жуковский)
Слайд 2 Математика – царица всех наук, символ
мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства.
Это не только стройная система законов, но и уникальное средство познания красоты.
Это не только стройная система законов, но и уникальное средство познания красоты.
«Математика есть прообраз красоты мира»
(В.Гейзенберг)
Слайд 3
Люди придумали цифры и действия с ними, а потом в них
же открыли множество законов, правил и теорем.
В жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач.
В жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач.
Числа живут своей жизнью, и мы, соприкоснувшись с ней, удивляемся, а иногда и любуемся ею.
Слайд 41 x 8 + 1 = 9 12 x 8 + 2
= 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 987 65
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
Математика - это красота и чудо в чистом виде.
Математическая пирамида №1
Какие вычисления будут выполнены в следующей строке и в последующих?
Слайд 5 1x 9 + 2 = 11 12 x 9 + 3
= 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111
Математика - это единственная наука, которая имеет дело с абсолютным идеалом.
Математическая пирамида №2
Какие вычисления будут выполнены в следующей строке и в последующих?
Слайд 69 x 9 + 7 = 88 98 x 9 + 6
= 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
Замечательно! Не правда ли?
Математическая пирамида №3
Какие вычисления будут выполнены в следующей строке и в последующих?
Слайд 71 x 1 = 1 11 x 11 = 121 111 x 111
= 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
Математика в своей сущности достаточно таинственна и романтична.
Математическая пирамида №4
Какие вычисления будут выполнены в следующей строке и в последующих?
Слайд 8Возьмем число 142857.
Удвоим его.
Получилось 285714.
Внимательно вглядываемся —
числа те
же, только в другом порядке!
б) Интересно, а если утроить? Учетверить?
Получаем последовательно:
428571, 571428, 714285, 857142.
Наша закономерность продолжает выполняться.
Цифры просто переставляются местами.
Красиво.!
б) Интересно, а если утроить? Учетверить?
Получаем последовательно:
428571, 571428, 714285, 857142.
Наша закономерность продолжает выполняться.
Цифры просто переставляются местами.
Красиво.!
Это интересно
Слайд 9Поверхности второго порядка. Загадочная красота.
эллипсоид
гиперболический параболоид
эллиптический параболоид
двуполостный гиперболоид
Слайд 10«...быть прекрасным значит быть симметричным и соразмерным»
(Платон)
Симметрия - закономерное расположение элементов формы относительно плоскости, оси или точки. Человек давно осмыслил симметрию в творениях природы и стал использовать се как средство организации искусственных форм. В Древней Греции слово "симметрия" было синонимом красоты, гармонии формы.
Слайд 11
Тадж-Махал — мавзолей-мечеть, находящийся в Агре, Индия, на берегу реки Ямуна.
Усыпальница имеет центральную симметрию относительно гробницы Мумтаз-Махал. Единственным нарушением этой симметрии является гробница Шах-Джахана, которую там соорудили после его смерти.
Слайд 12
Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Древнегреческие архитекторы
были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. Выбирая симметричные формы, художник тем самым выражал свое понимание природной гармонии как устойчивости, спокойствия и равновесия.
Слайд 13
Зеркальная симметрия
Если преобразование симметрии относительно плоскости переводит фигуру
в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры. В некоторых источниках такую симметрию называют зеркальной. А зеркало не просто копирует объект, но и меняет местами передние и задние по отношению к зеркалу части объекта.
Слайд 14
Симметрия в природе
Симметрия широко распространена в природе. Ее можно наблюдать
в форме листьев и цветов растений, в расположении различных органов животных.
Слайд 15Рассматривая расположение листьев на ветке дерева, видим, что один лист не
только отстоит от другого, но и повёрнут вокруг оси ствола. Листья располагаются на стволе по винтовой линии (принцип винтовой симметрии). Семена подсолнечника располагаются по спиралям, опять же по принципу симметрии.
Симметрия в природе
Красота растений привлекала внимание математиков веками. Активнее всего изучались интересные геометрические свойства растений, такие как симметрия листьев относительно центральной оси, радиальная симметрия цветов, и спиральное расположение семечек в шишках. Красота связана с симметрией.
Слайд 16В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это
маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.
Симметрия в неживой природе
Слайд 17
О, симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты
в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
Симметрия является фундаментальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений.
Слайд 18В 1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил
математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов.
Аристид Линденмайер
Слайд 19Rewriting — это способ получения сложных объектов путем замены частей простого
начального объекта по некоторым правилам. Классическим примером является снежинка. На рисунке initiator — это начальный объект, грани которого заменяются на generator. Далее с новым объектом проделывается то же самое.
Rewriting
Слайд 20Его красота в непериодичности. Любой сколь угодно большой фрагмент узора повторяется
бесконечное число раз, однако, нет таких двух точек где узор наложился бы сам на себя полностью (как не крути).
Замощение Пенроуза
Слайд 21Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного
треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево.
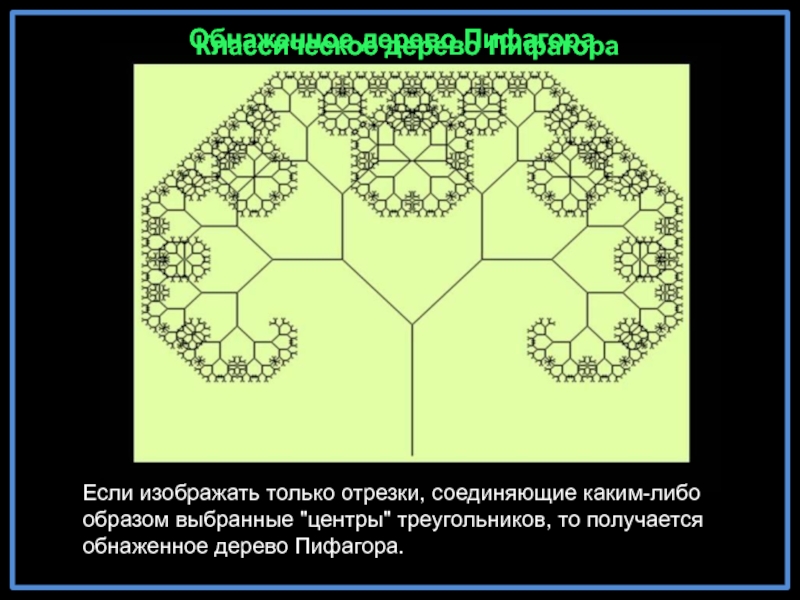
Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку.
Одним из свойств дерева Пифагора является то, что, если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
Дерево Пифагора
Слайд 22
Обнаженное дерево Пифагора
Классическое дерево Пифагора
Если изображать только отрезки, соединяющие каким-либо образом
выбранные "центры" треугольников, то получается обнаженное дерево Пифагора.
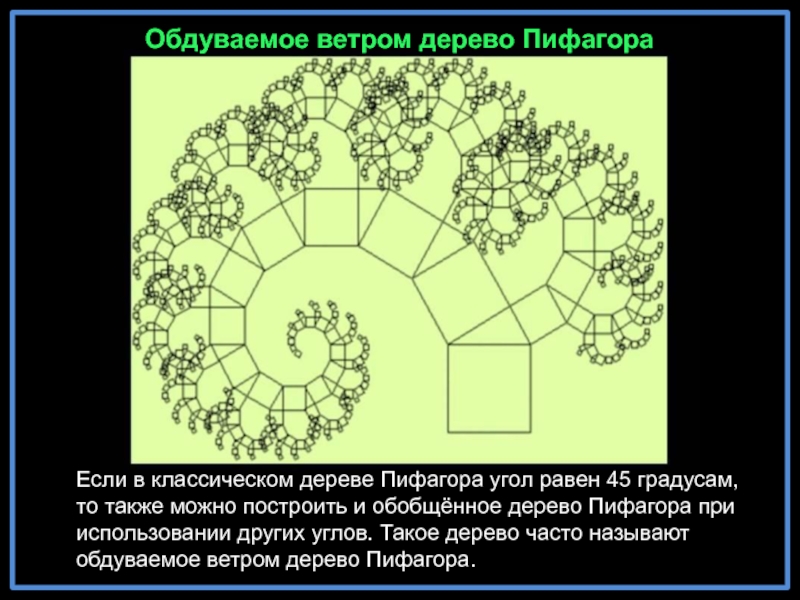
Слайд 23Обдуваемое ветром дерево Пифагора
Если в классическом дереве Пифагора угол равен 45
градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют обдуваемое ветром дерево Пифагора.
Слайд 25Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке
(например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы». Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому"
История
Красота есть истина, а истина — красота.
Джон Китс
Слайд 26Они кажутся более живыми и красивыми, чем многие рисунки, несмотря на
то, что являются результатом работы программы.
Галерея изображений фракталов
Слайд 27
Пифагор создал свою школу мудрости, положив в ее основу два искусства
- музыку и математику. Он считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Пифагор говорил своим ученикам, что числа правят миром.
Математика и музыка - два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.
Математическая музыка
Дроби широко используются в музыке для обозначения длительностей нот.
Слайд 28Эта последовательность имеет следующий вид: 1,1,2,3,5,8,13,21,...
То есть каждое последующее число
равно сумме двух предыдущих. При этом в пределе деление каждого числа на предыдущее даёт приблизительно 1,618 - это число и определяет "золотое сечение".
Золотое сечение
Средневековая математика подарила нам понятие о "золотом сечении" и последовательности Фибоначчи.
Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.
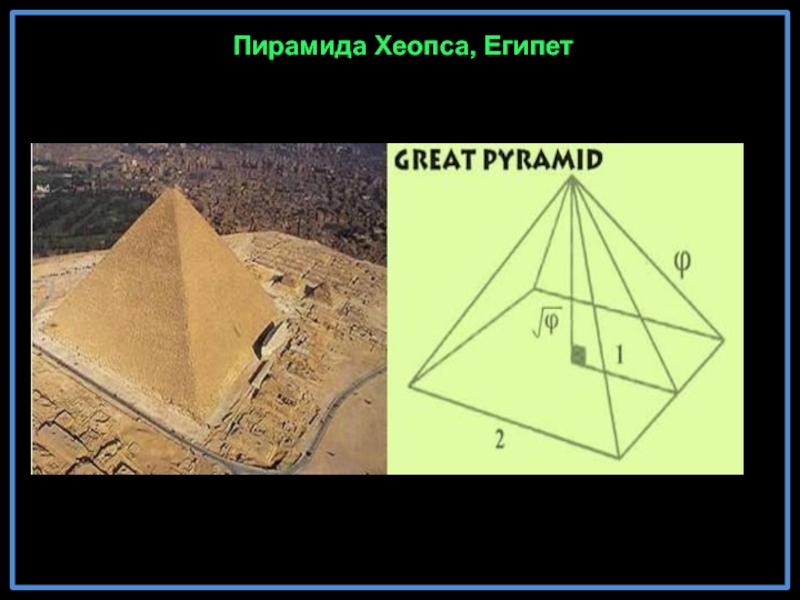
Слайд 29Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) —
деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
"Золотое сечение" в конструкции Парфенона, Афины, Греция
Собор "Нотредам де Пари" в Париже, Франция
Золотое сечение
Слайд 31
Еще Гете подчеркивал тенденцию природы к спиральности. Выяснилось, что в расположении
листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль "кривой жизни".
Пропорции Фибоначчи в природе
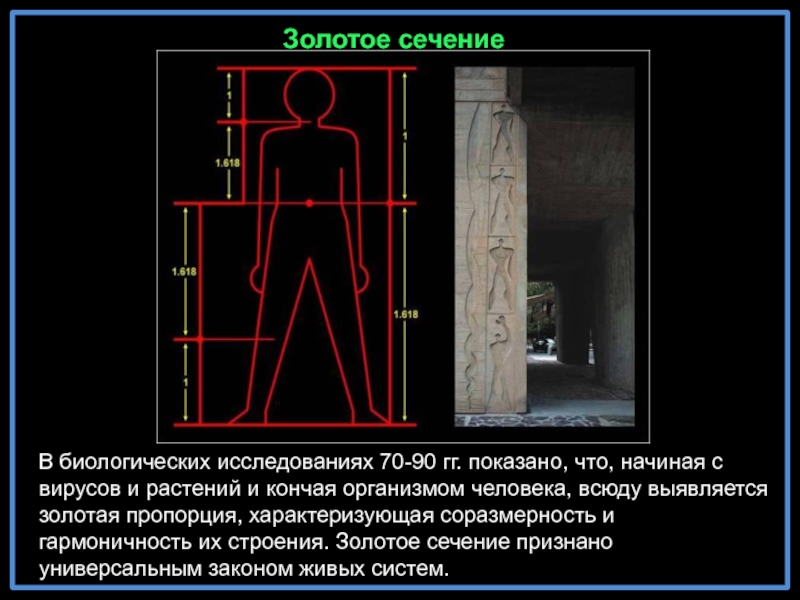
Слайд 32В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и
растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.
Золотое сечение
Слайд 34Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении
некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом.
Золотое сечение
Слайд 35
В математике есть тоже своя красота, как в живописи и поэзии.
Эта красота проявляется иногда в отчетливых, ярко очертанных идеях, где на виду всякая деталь умозаключения, а иногда поражает она нас в широких замыслах, скрывающих в себе кое-что недосказанное, но многообещающее. (Н.Е. Жуковский )
Математик так же, как художник или поэт, создаёт узоры…
Слайд 36Использованные ресурсы:
http://mcs.open.ac.uk/ugg2/jpg/med_RS_0065.jpg
http://en.wikipedia.org/wiki/Penrose_tiling
http://habrahabr.ru/blogs/biotech/69989
http://ru.wikipedia.org/wiki/http://ru.wikipedia.org/wiki/Фрактал
http://fractals.narod.ru/intro.htm
http://www.wack.ch/frac/gallery.html
http://www.ug.ru/issue/?action=topic&toid=8652
http://www.mathematics.ru/
«Математика и искусство», А. В. Волошинов, Москва, “Просвещение”, 2000г.
«Математическое путешествие
в мир гармонии», Е.С.Смирнова, Н.А. Леонидова, журнал «Математика в школе» № 3, 1993г.
Спасибо за внимание!
