- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад научной работы Таңғажайып жай сандар
Содержание
- 1. Презентация научной работы Таңғажайып жай сандар
- 2. Жай сандар туралы түсінікті кеңейтуЖай сандар теориясының
- 3. «Әлемде үйлесімділік орнаған және бұл үйлесімділік
- 4. Теориялық мәліметтерЖай сан- тек екі бөлгіші бар
- 5. Ең үлкен жай санды табуға бола ма?Ежелгі
- 6. Ең үлкен жай
- 7. Жай сандар тарихынанЭратосфен Киренский б.э.д 267- 194жжЭратосфен
- 8. Эратосфен елегіЭратосфен балауыздан
- 9. 1000ға дейінгі жай сандар кестесі
- 10. 1000 ға дейін 168 жай сан, 35
- 11. Жай сандар теориясының әртүрлі салаларда қолданылуыЖай сандар
- 12. Ұсыныс Мен тақырып аясында зерттеулер жүргізе
- 13. ҚорытындыЖай сандардың қасиеттері мен заңдылықтарын зерттей келе,
- 14. Назарларыңызға рахмет!
Слайд 1Маңғыстау облысы, Жаңаөзен қаласы
Таңғажайып жай сандар
Орындаған: Куттыхожа Әсел, «Дарын»
Ғылыми жетекшісі: Маханова Кулаш
Слайд 2Жай сандар туралы түсінікті кеңейту
Жай сандар теориясының даму тарихымен, әртүрлі салада
Жай сандарды табудың әдістері туралы жалпы түсінік қалыптастыру
Ұлы ғалымдардың жай сандар теориясы саласындағы жетістіктерін білу
1ден 1000ға дейінгі натурал сандар қатарынан «Эратосфен елегі» әдісімен жай сандарды алу қағидасын түсіну
Мақсаты мен мәселелері:
Слайд 3 «Әлемде үйлесімділік орнаған және бұл үйлесімділік сандарда анық көрінген»
«Сан – математика ғылымының іргетасы» деп қазақ математигі Орынбек Жәутіков атамыз айтқандай, бізді жан-жақтан сандар қоршайды, олар бізге барлық жерде қажет.
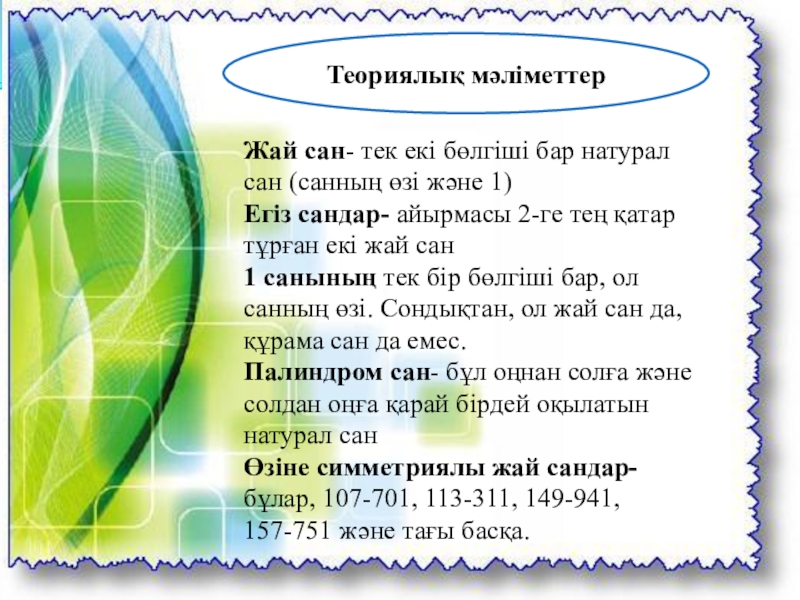
Слайд 4Теориялық мәліметтер
Жай сан- тек екі бөлгіші бар натурал сан (санның өзі
Егіз сандар- айырмасы 2-ге тең қатар тұрған екі жай сан
1 санының тек бір бөлгіші бар, ол санның өзі. Сондықтан, ол жай сан да, құрама сан да емес.
Палиндром сан- бұл оңнан солға және солдан оңға қарай бірдей оқылатын натурал сан
Өзіне симметриялы жай сандар- бұлар, 107-701, 113-311, 149-941, 157-751 және тағы басқа.
Слайд 5Ең үлкен жай санды табуға бола ма?
Ежелгі грек математигі Евклид
(б.э.д
Евклид өзінің «Бастау» деген кітабында жай сандардың шексіздігін, яғни ең үлкен жай санды табу мүмкін еместігін айтып кеткен.
Слайд 6 Ең үлкен жай сан
2 147 483 647 жай санын
243112609-1 жай санын 2009 жылы АҚШтың Орталық Миссури Университетінің ғалымы Кортис Купер тапты.
257885161-1 жай санын 2013 жылы америкалық ғалым Кортис Купер тауып, рекордын жаңартты.
277232917-1 жай санын 2017 жылы 51 жастағы америкалық инженер-электрик Джонатан Пейс тапты.
Слайд 7Жай сандар тарихынан
Эратосфен Киренский
б.э.д 267- 194жж
Эратосфен Кирен қаласында туылды;
Үлкен египет қалалары
Б.э.д 246 Птолемей Эвергет патшасы Эратосфенді Александрия кітапханасының жетекшісі етіп тағайындады;
Эратосфен өз заманының ең сауатты адамы болды. Ол математика және астрономиямен қатар, тарих пен философияны терең зерттеді, өлең жазып, музыкамен де шұғылданды.
Слайд 8 Эратосфен елегі
Эратосфен балауыздан жасалған тақтайшада құрама сандарды
Слайд 101000 ға дейін 168 жай сан, 35 егіз сандар жұбы, 16
Жай сандардың қасиеттері мен заңдылықтары