- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Начальный курс по подготовке к олимпиадам по математике
Содержание
- 1. Презентация Начальный курс по подготовке к олимпиадам по математике
- 2. Часть 2. Задание 19 Арифметика и алгебра
- 3. Часть 2. Задание 19 Арифметика и алгебра
- 4. 1. Натуральные числа Множество положительных целых чисел
- 5. Четность, нечетность Число, делящееся нацело на два,
- 6. Четность, нечетность Число, делящееся нацело на два,
- 7. Четность, нечетность Число, делящееся нацело на два,
- 8. Четность, нечетность Число, делящееся нацело на два,
- 9. Четность, нечетность Число, делящееся нацело на два,
- 10. Четность, нечетность Число, делящееся нацело на два,
- 11. Четность, нечетность Число, делящееся нацело на два,
- 12. Четность, нечетность Число, делящееся нацело на два,
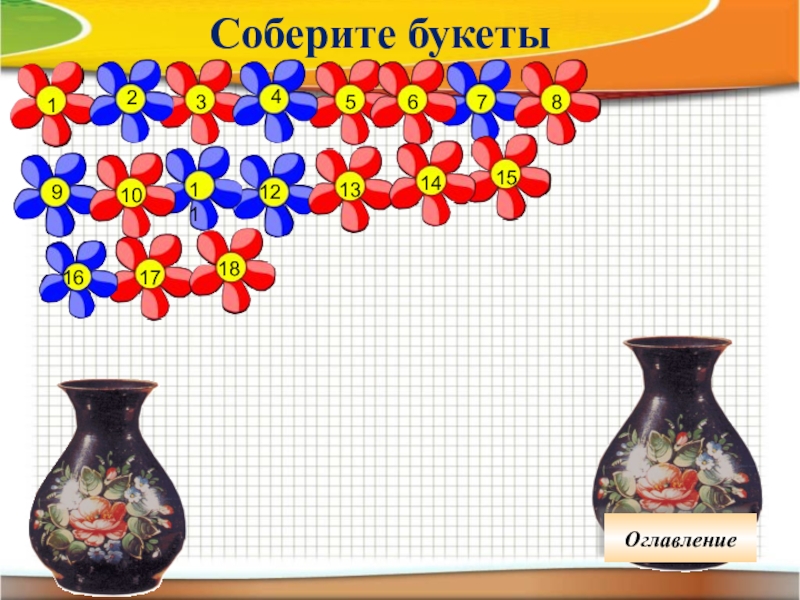
- 13. 371131511517928101214161846Соберите букетыОглавление
- 14. Решение задач 1. Лягушка прыгала по прямой
- 15. 2. Сумма трех чисел – нечетное число.
- 16. 4. Шестеренки расставлены по кругу. Какое из колес будет крутиться?1212Оглавление
- 17. 4. Шестеренки расставлены по кругу. Какое из колес будет крутиться?12Оглавление
- 18. 5. Лягушка прыгает по прямой. За один
- 19. 6. Квадрат 9 Х 9 раскрашивают в
- 20. Осталось по одному цвету, которые надо расставить
- 21. 6. Квадрат 100 Х 100 разбит на
- 22. 7. 8 лампочек с кнопками включения расположены
- 23. 7. 200 лампочек с кнопками включения расположены
- 24. 8. В каждой вершине n – угольника
- 25. 8. В каждой вершине n – угольника
- 26. Задача 1. На листе бумаги написано число 11.
- 27. Задача 5. На столе 6 стаканов, Из них
- 28. 371131511517928101214161846Букеты из четных и нечетных цветовЛюбое число, делящееся на два, можно назвать четным.Оглавление
- 29. Действительные числа Действительные числаНатуральные числаЦелые числаЦелые положительные
- 30. Делимость. Признаки делимости a : b
- 31. Задача 1. Найдите делители от 2 до
- 32. Простые и составные числа Натуральные числа, имеющие
- 33. Простые и составные числа Натуральные числа, имеющие
- 34. Разложение числа на простые множители 1) 12
- 35. Наибольший общий делитель Число, на которое делится
- 36. Наименьшее общее кратное Число, которое делится на
- 37. В задаче 1. найдены простые множители 2,
- 38. Взаимно простые числа Числа а и b
- 39. Периодичность последней цифры при возведении в степень
- 40. Задача 3. Определите на какую цифру оканчивается
- 41. Деление с остатком 1374312174161Остаток137 = 4 ·
- 42. Периодичность остатков при делении на натуральное число
- 43. Периодичность остатков при делении на натуральное число
- 44. Периодичность остатков при делении на натуральное число
- 45. Задача 6. Существует ли такое натуральное число
- 46. Рациональные числа т – целое число; п – натуральное числоМножество рациональных чисел - QОглавление
- 47. Обыкновенная дробь Основное свойство дроби Значение дроби
- 48. Задача 5. Докажите, что дробь
- 49. Десятичная запись числа Всякое натуральное число может
- 50. Делится на 920102 10053 6752010 = 2
- 51. abcd + abc + ab + а
- 52. Метод математической индукции Индукция – это переход
- 53. 1 + 3 + 5 … +
- 54. п = 1- верно п = k-
- 55. Задача 12. Докажите, что 1 +23 +
- 56. Задача 13. Найдите сумму Сначала необходимо выявить
- 57. Задача 14. Докажите, что для любого натурального
- 58. Решение уравнений в целых числах Уравнение, содержащее
- 59. Задача 15. В клетке находятся кролики и
- 60. Уравнение ах + bу = с имеет
- 61. Формулы решения уравнения ax + bx =
- 62. Решите уравнение -23х + 79у = 1
- 63. Решение нелинейных уравнений Метод разложения на множители
- 64. Метод решения уравнения относительно одной из переменных
- 65. Задача 19. Решите уравнение 3(х2 + ху
- 66. Задача 20. Решите уравнение x2 – xy
- 67. Метод последних цифр при возведении в степень
- 68. Заметим, что периодичность последних цифр у 3п
- 69. Метод оценок Задача 22. Решите уравнение 2х2
- 70. Метод оценок Задача 22. Решите уравнение 2х2
- 71. Метод приведения к сумме положительных чисел Задача
- 72. Принцип ДирихлеВ несерьёзной форме принцип Дирихле гласит:
- 73. Принцип Дирехле «Нельзя посадить 7 кроликов в
- 74. Принцип Дирехле хотя бы в одной клетке
- 75. Принцип Дирехле хотя бы одна клетка останется
- 76. Решение задач по принципу Дирехле Таким образом,
- 77. 1.В классе 15 учеников. Докажите, что найдутся,
- 78. 3. В 8 «Б» классе учится 27
- 79. 5. Внутри равностороннего треугольника со стороной 1см
- 80. Последовательности Числовая последовательность – это набор чисел,
- 81. Свойства арифметической прогрессии аn = kn +
- 82. Геометрическая прогрессия Геометрическая прогрессия – это последовательность,
- 83. Свойства геометрической прогрессии bn = kan -
- 84. 6. Доказать, что среди разных шести целых
- 85. 7. Доказать, что число N5 оканчивается на
- 86. 8. В коробке лежат шарики 4-х разных
- 87. 9. Сколькими способами можно поставить на доску
- 88. 9. Сколькими способами можно поставить на доску
- 89. 10. Сколькими способами можно поставить на доску
- 90. Решение логических задач Пример 1. В симфонический
- 91. Пример 2. Три одноклассника — Влад, Тимур
- 92. Пример 5. Три дочери писательницы Дорис Кей
- 93. Пример 3. Вадим, Сергей и Михаил изучают
- 94. Пример 3. Вадим, Сергей и Михаил изучают
- 95. Пример 3. Вадим, Сергей и Михаил изучают
Слайд 2Часть 2. Задание 19
Арифметика и алгебра
1. Теория чисел
2. Делимость.
3. Простые и составные числа
4.. Деление с остатком. НОД и НОК
5. Обыкновенная дробь. Сократимость.
6. Десятичная запись числа.
7. Метод математической индукции.
8. Методы решения уравнений в целых числах.
9. Принцип Дирихле.
Слайд 3Часть 2. Задание 19
Арифметика и алгебра
10. Последовательности. Арифметическая и
11. Решение логических задач.
В режиме демонстрации прейдите к оглавлению
Оглавление
Проверь себя
Перейти к оглавлению
Проверить свое решение
Справка
Переход к справочному материалу
Слайд 41. Натуральные числа
Множество положительных целых чисел называется натуральными числами
1
2
5
67
234
18
Обозначение:
N
При работе с натуральными числами используются прописные латинские буквы: n, m, k, l и т.д.
Оглавление
Слайд 5Четность, нечетность
Число, делящееся нацело на два, называется четным, остальные –
n = 2k, где k принадлежит N -
четное число
n = 2k +1, где k принадлежит N -
нечетное число
Свойства четности, нечетность
1. Сумма двух четных чисел -
четное число
нечетное число
Оглавление
Слайд 6Четность, нечетность
Число, делящееся нацело на два, называется четным, остальные –
n = 2k, где k принадлежит N -
четное число
n = 2k +1, где k принадлежит N -
нечетное число
Свойства четности, нечетность
1. Сумма двух четных чисел -
2. Сумма двух нечетных чисел -
четное число
нечетное число
четное число
Оглавление
Слайд 7Четность, нечетность
Число, делящееся нацело на два, называется четным, остальные –
n = 2k, где k принадлежит N -
четное число
n = 2k +1, где k принадлежит N -
нечетное число
Свойства четности, нечетность
1. Сумма двух четных чисел -
2. Сумма двух нечетных чисел -
четное число
нечетное число
четное число
3. Сумма четного и нечетного чисел -
четное число
Оглавление
Слайд 8Четность, нечетность
Число, делящееся нацело на два, называется четным, остальные –
n = 2k, где k принадлежит N -
четное число
n = 2k +1, где k принадлежит N -
нечетное число
Свойства четности, нечетность
1. Сумма двух четных чисел -
2. Сумма двух нечетных чисел -
четное число
нечетное число
четное число
3. Сумма четного и нечетного чисел -
четное число
нечетное число
Оглавление
Слайд 9Четность, нечетность
Число, делящееся нацело на два, называется четным, остальные –
n = 2k, где k принадлежит N -
четное число
n = 2k +1, где k принадлежит N -
нечетное число
Свойства четности, нечетность
1. Произведение двух четных чисел -
четное число
нечетное число
Оглавление
Слайд 10Четность, нечетность
Число, делящееся нацело на два, называется четным, остальные –
n = 2k, где k принадлежит N -
четное число
n = 2k +1, где k принадлежит N -
нечетное число
Свойства четности, нечетность
1. Произведение двух четных чисел -
2. Произведение двух нечетных чисел -
четное число
нечетное число
четное число
Оглавление
Слайд 11Четность, нечетность
Число, делящееся нацело на два, называется четным, остальные –
n = 2k, где k принадлежит N -
четное число
n = 2k +1, где k принадлежит N -
нечетное число
Свойства четности, нечетность
1. Произведение двух четных чисел -
2. Произведение двух нечетных чисел -
четное число
нечетное число
четное число
3. Произведение четного и нечетного чисел -
нечетное число
Оглавление
Слайд 12Четность, нечетность
Число, делящееся нацело на два, называется четным, остальные –
n = 2k, где k принадлежит N -
четное число
n = 2k +1, где k принадлежит N -
нечетное число
Свойства четности, нечетность
1. Произведение двух четных чисел -
2. Произведение двух нечетных чисел -
четное число
нечетное число
четное число
3. Произведение четного и нечетного чисел -
четное число
четное число
Оглавление
Слайд 14Решение задач
1. Лягушка прыгала по прямой и вернулась обратно. Длина
Решение. Нет.
Чтобы вернуться назад, лягушка должна сделать столько же прыжков, сколько их сделала вперед.
Пусть лягушка сделала n прыжков. Тогда обратно должна сделать тоже n прыжков, т.е. 2n прыжка. Это четное число.
Оглавление
Слайд 152. Сумма трех чисел – нечетное число. Сколько слагаемых нечетно?
Решение
Пусть числа
Тогда возможно:
а + а + а
а + а + b
а + b + b
b + b + b
= 6n
= 4n + 1
= 4n + 2
= 6n + 3
нечетно
нечетно
Ответ: 1, 3
3. Определите четность суммы: 1 + 2 + 3 +…+ 1999
Для решения используем более короткий ряд: 1 + 2 + 3 + 4 + 5 +6 + 7 + 8 + 9
В ряду 4 пары – нечетное, четное. Их сумма – число четное (нечетное умножить на четное равно четному числу).
Плюс нечетное число. Сумма будет нечетна.
В ряду 1 + 2 + 3 +…+ 1999 999 пар (1998 : 2) – нечетно. Сумма – нечетна (нечетное умножить на нечетное равно нечетному числу).
Последнее число нечетно, следовательно сумма будет четна
Оглавление
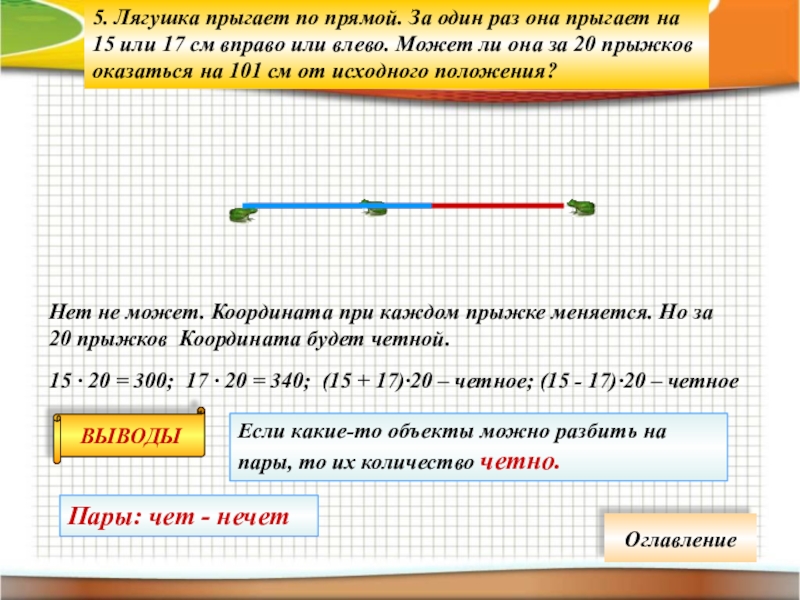
Слайд 185. Лягушка прыгает по прямой. За один раз она прыгает на
Нет не может. Координата при каждом прыжке меняется. Но за 20 прыжков Координата будет четной.
15 · 20 = 300; 17 · 20 = 340; (15 + 17)·20 – четное; (15 - 17)·20 – четное
ВЫВОДЫ
Если какие-то объекты можно разбить на пары, то их количество четно.
Пары: чет - нечет
Оглавление
Слайд 19
6. Квадрат 9 Х 9 раскрашивают в 9 цветов так, чтобы
Раскрасим симметрично относительно диагонали клетки. Будем брать по паре одного цвета.
Оглавление
Слайд 20
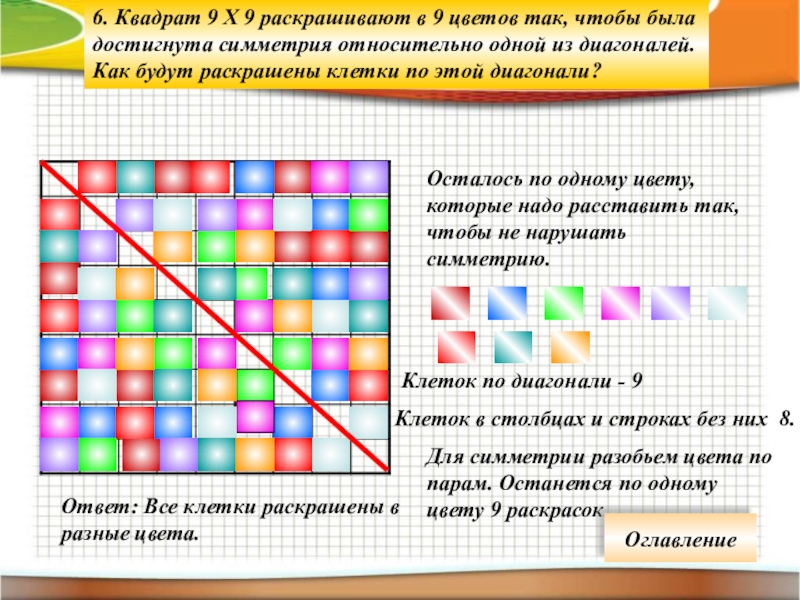
Осталось по одному цвету, которые надо расставить так, чтобы не нарушать
Ответ: Все клетки раскрашены в разные цвета.
6. Квадрат 9 Х 9 раскрашивают в 9 цветов так, чтобы была достигнута симметрия относительно одной из диагоналей. Как будут раскрашены клетки по этой диагонали?
Клеток по диагонали - 9
Клеток в столбцах и строках без них 8.
Для симметрии разобьем цвета по парам. Останется по одному цвету 9 раскрасок.
Оглавление
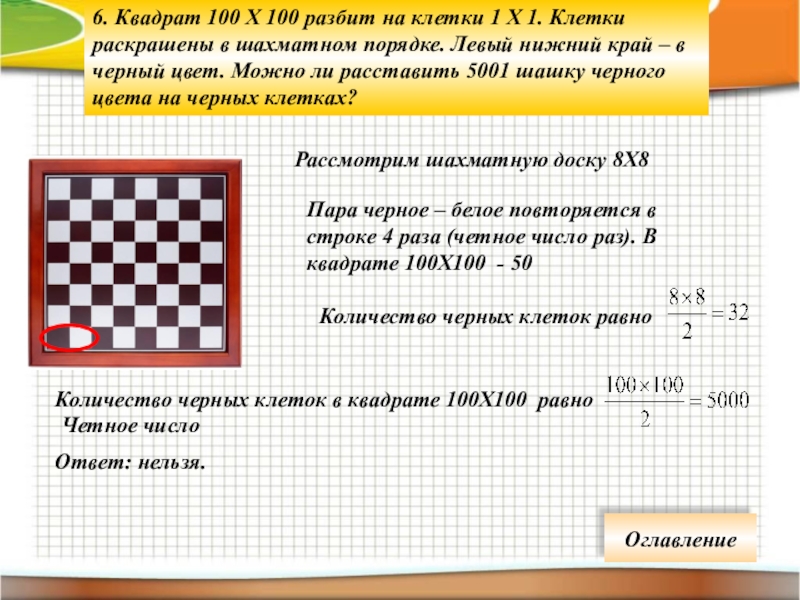
Слайд 216. Квадрат 100 Х 100 разбит на клетки 1 Х 1.
Рассмотрим шахматную доску 8Х8
Пара черное – белое повторяется в строке 4 раза (четное число раз). В квадрате 100Х100 - 50
Ответ: нельзя.
Четное число
Оглавление
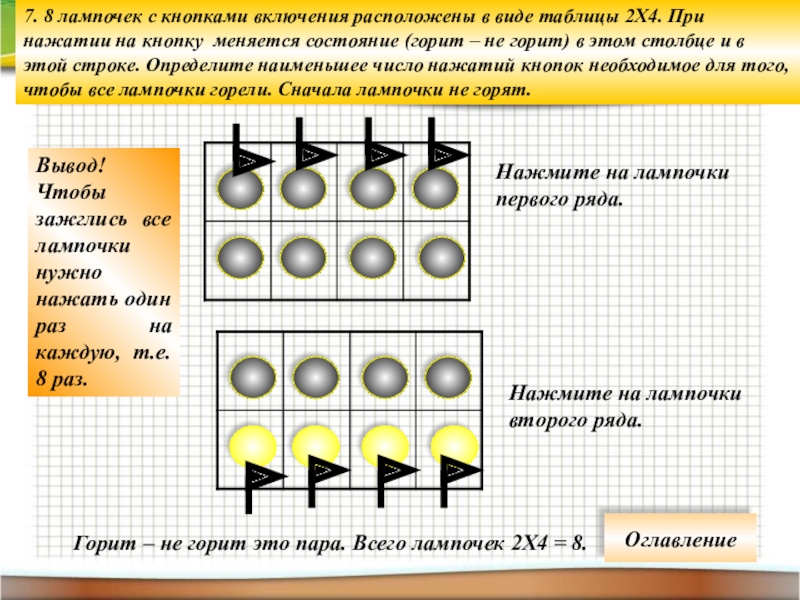
Слайд 227. 8 лампочек с кнопками включения расположены в виде таблицы 2Х4.
Нажмите на лампочки первого ряда.
Нажмите на лампочки второго ряда.
Вывод! Чтобы зажглись все лампочки нужно нажать один раз на каждую, т.е. 8 раз.
Горит – не горит это пара. Всего лампочек 2Х4 = 8.
Оглавление
Слайд 237. 200 лампочек с кнопками включения расположены в виде таблицы 50Х40.
а) Всего 50Х40 =2000
б) Всего 89
40 + 50 = 90, 90 – 1 = 89
Оглавление
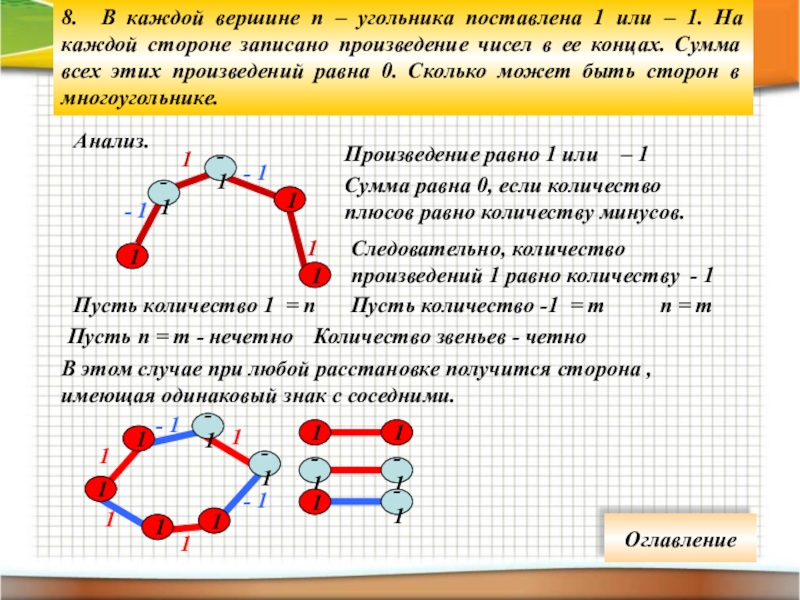
Слайд 248. В каждой вершине n – угольника поставлена 1 или –
Анализ.
Произведение равно 1 или – 1
Сумма равна 0, если количество плюсов равно количеству минусов.
- 1
1
- 1
1
1
- 1
1
- 1
1
1
1
1
-1
1
Следовательно, количество произведений 1 равно количеству - 1
Пусть количество 1 = n
Пусть количество -1 = m
Пусть n = m - нечетно
Количество звеньев - четно
n = m
В этом случае при любой расстановке получится сторона , имеющая одинаковый знак с соседними.
1
-1
1
-1
1
Оглавление
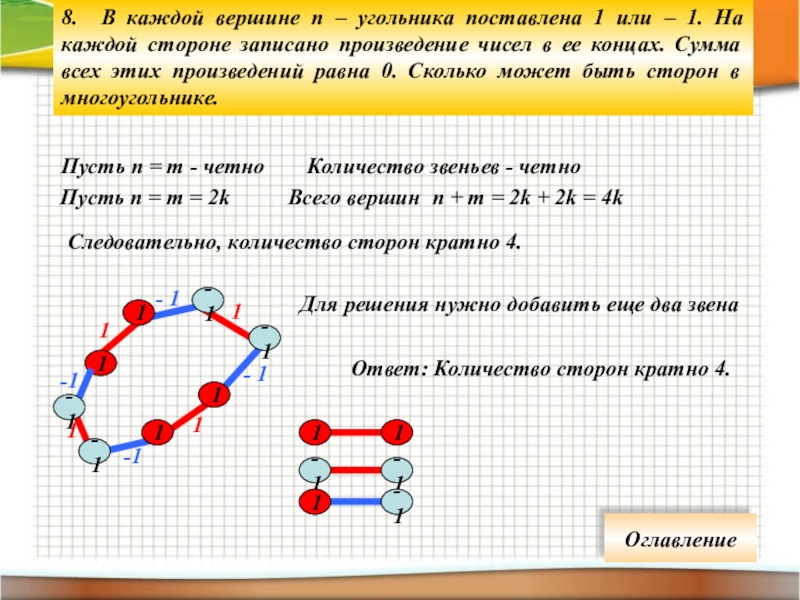
Слайд 258. В каждой вершине n – угольника поставлена 1 или –
1
-1
-1
-1
1
Пусть n = m - четно
Количество звеньев - четно
Пусть n = m = 2k
Всего вершин n + m = 2k + 2k = 4k
Следовательно, количество сторон кратно 4.
Для решения нужно добавить еще два звена
-1
-1
-1
-1
Ответ: Количество сторон кратно 4.
Оглавление
Слайд 26Задача 1. На листе бумаги написано число 11. Шестнадцать учеников передают листок
Задача 2. На вешалке висят 20 платков. 17 девочек по очереди подходят к вешалке и либо снимают, либо вешают платок. Может ли после ухода девочек остаться ровно 10 платков?
Задача 3. В таблице, где имеются 15 отрицательных чисел , можно производить следующую операцию: одновременно изменить знак двух (не более, не меньше) чисел в таблице. Можно ли, применяя эту операцию конечное число раз, получить таблицу, состоящую из всех положительных чисел?
Задача 5. На столе 6 стаканов, Из них 5 стоят правильно, а один перевернут вверх дном. Разрешается переворачивать одновременно 4 любых стакана. Можно ли все стаканы поставить правильно?
Решаем самостоятельно
Оглавление
Слайд 27Задача 5. На столе 6 стаканов, Из них 5 стоят правильно, а
Задача 6. На доске записано 15 чисел: 8 нулей и 7 единиц. Вам предлагается 14 раз подряд выполнить такую операцию: зачеркнуть любые два числа и если они одинаковые, то дописать к оставшимся числам нуль, а если разные, то единицу. Какое число останется на доске?
Задача 7. В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки «+» и «—» так, чтобы значение полученного выражения было равно нулю?
8. Катя и ее друзья встали по кругу. Оказалось, что оба соседа каждого ребенка – одного пола. Мальчиков среди Катиных друзей пять. А сколько девочек?
Оглавление
Слайд 283
7
1
13
15
11
5
17
9
2
8
10
12
14
16
18
4
6
Букеты из четных и нечетных цветов
Любое число, делящееся на два, можно
Оглавление
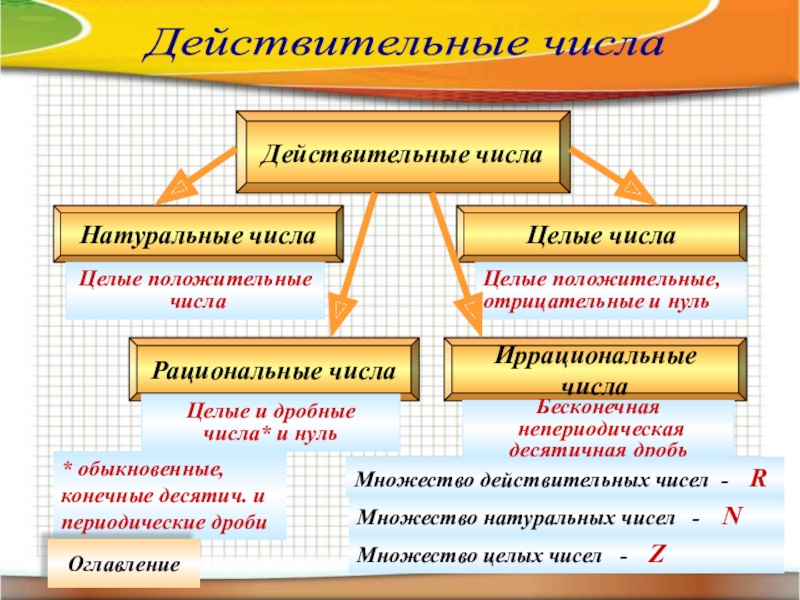
Слайд 29Действительные числа
Действительные числа
Натуральные числа
Целые числа
Целые положительные
числа
Целые положительные,
отрицательные и
Рациональные числа
Иррациональные числа
Целые и дробные
числа* и нуль
Бесконечная
непериодическая
десятичная дробь
Множество действительных чисел - R
Множество натуральных чисел - N
Множество целых чисел - Z
* обыкновенные, конечные десятич. и периодические дроби
Оглавление
Слайд 30Делимость. Признаки делимости
a : b = q
a =
a : b
Делимость натуральных чисел. Свойства
Оглавление
Слайд 31
Задача 1. Найдите делители от 2 до 10 числа п5
Чтобы найти делители, надо число разложить на множители
п5 – 5п3 + 4п = п(п4–5п2+4) = п(п4 –п2–4п2+4)=п((п–1)(п+1)(n -2)(n + 2)
Расположим множители в порядке возрастания
( п – 2)(п – 1)п(п + 1)(п + 2) – 5 последовательных натуральных чисел
Среди любых 5 – ти последовательных чисел найдутся числа, делящиеся
на 2k, 3m, 4l, 5 p
Делителями от 2 до 10 являются 2, 3, 4, 5
Оглавление
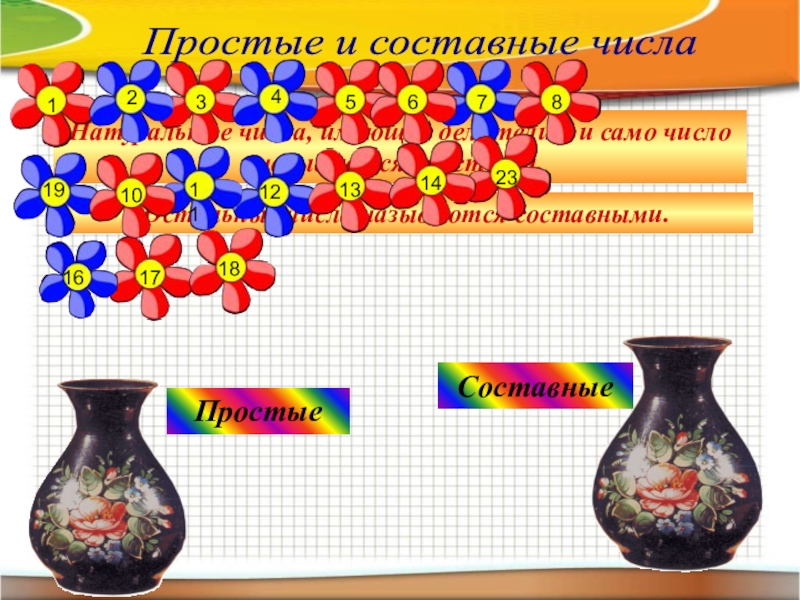
Слайд 32Простые и составные числа
Натуральные числа, имеющие делители 1 и само
Остальные числа называются составными.
Простые
Составные
Оглавление
Слайд 33Простые и составные числа
Натуральные числа, имеющие делители 1 и само
Остальные числа называются составными.
3
7
1
13
23
11
5
17
19
2
8
10
12
14
16
18
4
6
Простые
Составные
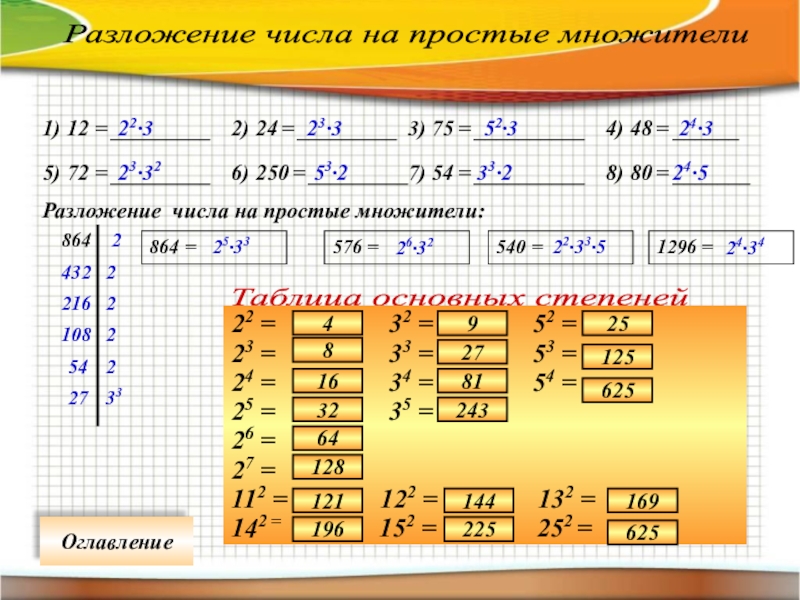
Слайд 34Разложение числа на простые множители
1) 12 = _________
2) 24 =
3) 75 = __________
4) 48 = ______
5) 72 = _________
6) 250 = _________
7) 54 = __________
8) 80 = _______
Разложение числа на простые множители:
864
22·3
23·3
52·3
24·3
23·32
53·2
33·2
24·5
2
432
2
216
2
108
2
54
2
27
33
Оглавление
Слайд 35
Наибольший общий делитель
Число, на которое делится каждое число ряда чисел,
НОД равен произведению общих множителей каждого числа ряда
Пример: Найдите НОД для чисел 45, 75, 120.
45 = 3·3· 5
75 = 3· 5·5
120 = 23 3· 5
Общие множители:
3 и 5
Берутся общие в меньшей степени
НОД(45,75,120) = 15
Все числа делятся на 15
Оглавление
Слайд 36
Наименьшее общее кратное
Число, которое делится на каждое число ряда чисел,
НОК равен произведению общих множителей каждого числа ряда
Пример: Найдите НОК для чисел 45, 75.
45 = 3·3· 5
75 = 3· 5·5
НОК(45,75) = 3·5·3·5 = 225
225 делится на 45 и 75
Из 45 не хватает множителя 3
Из 75 не хватает множителя 5
Для устного нахождения НОК можно взять наибольшее число и умножать его последовательно на 2, 3, 4 и т.д., до тех пор пока не получится число, которое делится на каждое.
НОК(30, 12)
30·2 = 60, 60 : 12 = 5 - делится
= 60
Берутся все множители в большей степени.
Оглавление
Слайд 38Взаимно простые числа
Числа а и b называются взаимно простыми, если
Пример: 35 и 12; 46 и 27; 3 и 5
Если а и b взаимно простые, то НОД(а, b) = ab
Оглавление
Слайд 39
Периодичность последней цифры при возведении в степень
21 = 2
22 = 4 26 = 64
23 = 8 27 = 128
24 =1 6 28 = 256
31 = 3 35 = 243
32 = 9 36 = 729
33 =27 37 = 2187
34 = 81 38 = 37·3
ВЫВОДЫ
Последняя цифра при возведении в степень натурального числа повторяется с периодичностью соответствующей ряду окончаний при последовательном возведении в степень.
Задача 3. Определите на какую цифру оканчивается число 22014
Известно, что окончаний при возведении 2n – 4( 2, 4, 8, 6)
Все окончания будут повторяться через 4. Период равен 4
Разделим 2014 на 4:
2014 : 4 = 503 и 2 в остатке
2, 4, 8, 6
Ответ: 4
Оглавление
Слайд 40Задача 3. Определите на какую цифру оканчивается число 22014
Известно:
21 =
22 = 4 26 = 64
23 = 8 27 = 128
24 =1 6 28 = 256
Окончаний 4: 2, 4, 8, 6
ВЫВОДЫ
Последняя цифра при возведении в степень натурального числа повторяется с периодичностью соответствующему ряду окончаний при последовательном возведении в степень
Оглавление
Слайд 41
Деление с остатком
137
4
3
12
17
4
16
1
Остаток
137 = 4 · 34 + 1
Целая часть
Если
a = bq + r
q – целая часть деления
r – остаток деления
Задача 4. Запишите число, делящееся на 3 и с остатком 2
Таких чисел множество: n = 3k + 2
Например, п = 3k + 2 означает, что число делится на 3 и в остатке 2.
Оглавление
Слайд 42Периодичность остатков при делении на натуральное число
Определим остатки при делении
ВЫВОДЫ
Если число делится на 2 с остатком, то этот остаток равен 1
Определим остатки при делении числа п на 3.
ВЫВОДЫ
Если число делится на 3 с остатком, то эти остатки могут быть 1 и 2
Оглавление
Слайд 43Периодичность остатков при делении на натуральное число
Определим остатки при делении
ВЫВОДЫ
Если число делится на 4 с остатком, то эти остатки 1, 2, 3
Определим остатки при делении числа п на 5.
ВЫВОДЫ
Если число делится на 5 с остатком, то эти остатки могут быть 1, 2, 3, 4
Оглавление
Слайд 44Периодичность остатков при делении на натуральное число
ВЫВОД
Если число п делится
Задача 5. Докажите, что квадраты натуральных чисел при делении на 3, не дают остаток 2
Остаток при делении п2 на 3 может быть только 1.
* Отметим. Одной таблиц не достаточно для решения. Нужно доказательство.
Так как остатки при делении на 1 или 2, то п = 3k + 1 или п = 3k + 2
п = 3k + 1. n2 = 9k2 + 6k + 1 = 3(3k2 + 2k) + 1 = 3m + 1
п = 3k + 2. n2 = 9k2 + 12k + 4 = 3(3k2 + 4k) + 4 = 3l + 4, но 4 делится на 3 с остатком 1. Следовательно, остаток может быть только 1.
Оглавление
Слайд 45
Задача 6. Существует ли такое натуральное число п, что
2015 делится на 5.
Рассмотрим деление с остатком числа п на 5.
Остатки: 1, 2, 3, 4
п = 5k + 1, тогда
п2 + п + 1 = 25k2 + 15k + 3 = 5l + 3 Остаток 3
п = 5k + 2, тогда
п2 + п + 1 = 25k2 + 25k + 7 = 5l + 7 Остаток 2
п = 5k + 3, тогда
п2 + п + 1 = 25k2 + 35k + 13 = 5l + 13 Остаток 3
п = 5k + 4, тогда
п2 + п + 1 = 25k2 + 45k + 21 = 5l + 17 Остаток 2
Число п не делится на 2015.
Оглавление
Слайд 46
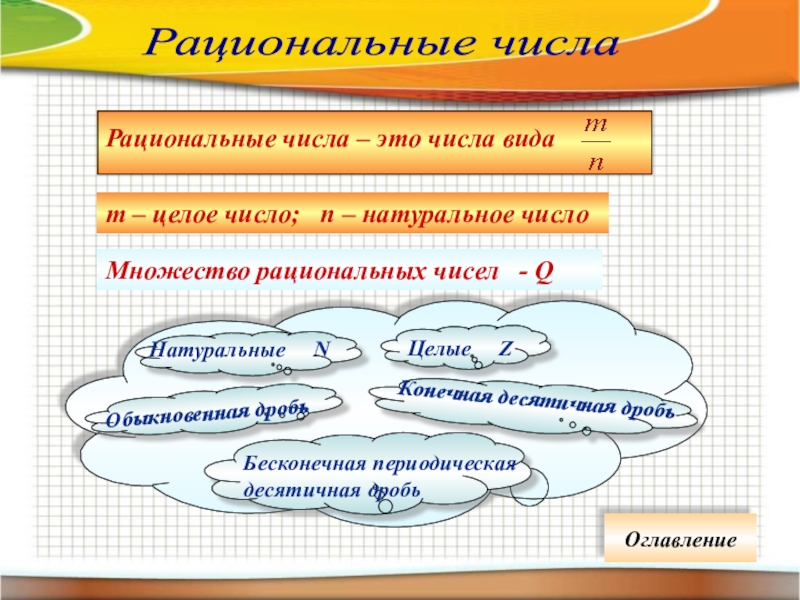
Рациональные числа
т – целое число; п – натуральное число
Множество
Оглавление
Слайд 47Обыкновенная дробь
Основное свойство дроби
Значение дроби не изменится, если числитель
Сокращение дробей
Сократить дробь – значит разделить числитель и знаменетель на общие множители.
Чтобы сократить дробь, надо разложить числитель и знаменатель на простые множители.
Несократимая дробь – дробь, не имеющая общих множителей.
Оглавление
Слайд 48
Задача 5. Докажите, что дробь
Приведем числитель и знаменатель к виду так, чтобы часть kn была бы одинаковой.
В числителе число n делится на 6 и
в остатке 3
В знаменателе число п делится на 6 и
в остатке 4
Пусть числитель и знаменатель делится q, q > 1, натуральное число.
k =
Заметим, что если два числа делятся на q, то их сумма или разность тоже делится на q
Делится на q, если q = 1. Противоречие. q > 1.
Оглавление
Слайд 49
Десятичная запись числа
Всякое натуральное число может быть представлено в виде:
п
Например, 123 = 3 + 2 · 10 + 1· 102 = 3 + 20 + 100
Требование десятичной записи обозначается чертой над числом. 123
п показывает разряд
Трехзначное число xyz представить в виде десятичной записи:
Оглавление
Слайд 50Делится на 9
2010
2
1005
3
67
5
2010 = 2 · 3 · 5
Заметим, что цифры в десятичной записи могут быть от 0 до 9
67 > 9. Не может.
335
Оглавление
Слайд 51abcd + abc + ab + а = 1000a+100b+10c+d+100a+10b+c+10a+b+a =
1111a+ 111b+11c+d = 2011
а может быть равно только 1 (1111) a = 1
с может изменяться от 0 до 9. 11с изменяется от 0 до 99
b может изменяться от 0 до 9. 111b изменяется от 0 до 999
Пусть b = 9, тогда 111b = 999. 1111 + 999 = 2110 > 2011
Пусть b = 8, тогда 111b = 888. 1111 + 888 = 1999 < 2011
11c + d = 2011 – 1999 = 12, следовательно, с = 1, d = 1
Оглавление
Слайд 52Метод математической индукции
Индукция – это переход от частного к общему.
Метод
Алгоритм
1. Доказательство, что утверждение верно для п = 1
2. Принятие за достоверное, что утверждение верно для n = k
3. Доказательство, что утверждение верно для п = k + 1
Оглавление
Слайд 531 + 3 + 5 … + (2п - 1) =
Шаг 1.
п = 1
1 = 12 - верно
Шаг 2. предположение
п = k
1 + 3 + 5 … + (2k - 1) = k2 - верно
Шаг 3. индуктивный переход.
п = k + 1
1 + 3 + 5 … + (2k + 1) = (k + 1)2
1 + 3 + 5 …+ (2k – 1) + (2k + 1) = (k + 1)2
{
k2
k2 + 2k + 1 = (k + 1)2 – верно
Выделим в выражении левой части выражение для n=k
Доказано.
{
Оглавление
Слайд 54п = 1
- верно
п = k
- верно
п = k
Выделим в выражении левой части выражение для n=k
{
2k2 + 7k + 6 = 2(k + 2)(k + 3/2) = (k + 2)(2k + 3)
Доказано.
Оглавление
Слайд 55
Задача 12. Докажите, что 1 +23 + 33 +…+ п3 =
п = 1
13 = 12
- верно
п = k
13 +23 +33+…+k3 = (1+2+3+…+k)2
- верно
п = k + 1
13 +23 +33+…+k3 +(k+1)3 = (1+2+3+…+k +(k+1))2
Вычтем из выражения для п = k + 1 выражение для п = k, получим (k + 1)3
(1+2+3+…+k +(k+1))2 - (1+2+3+…+k)2 = (k+1)(2(1+2+3+…+k) +(k+1))
a2
b2
(k + 1)3
Доказано.
{
{
-
Оглавление
Слайд 56
Задача 13. Найдите сумму
Сначала необходимо выявить закономерность и создать формулу
Докажем, что это так:
n = 1 S1 = ½ - верно
Доказано
Оглавление
Слайд 57
Задача 14. Докажите, что для любого натурального п 5п + 3
п = k + 1 5k + 1 + 3
Докажем, что выражение делится на 4
5k + 1 + 3 = 5 · 5k + 3 = 5 · 5k + 15 – 15 + 3 = 5(5k + 3) - 12
5k + 3 делится на 4
12 делится на 4
Следовательно, все число делится на 4
Оглавление
Слайд 58Решение уравнений в целых числах
Уравнение, содержащее несколько переменных и решаемое
Уравнение вида ах + bx = c
1. Метод перебора
Решите в натуральных числах уравнение 2х + 5у = 12
1) х =1
2· 1 + 5у = 12; у = 2
(1;2)
2) х =2
2· 2 + 5у = 12; у - дробное
3) х =3
2· 3 + 5у = 12; у - дробное
4) х =4
2· 4 + 5у = 12; у - дробное
5) х =5
2· 5 + 5у = 12; у - дробное
6) х =6
2· 6 + 5у = 12; у = 0
(6;0)
7) х > 6
2· 7 + 5у = 12; у < 0
Ответ: (1;2), (6;0)
Оглавление
Слайд 59
Задача 15. В клетке находятся кролики и фазаны. Всего у них
Пусть кроликов х, у них 4 ноги.
Пусть фазанов у, у них 2 ноги.
4х + 2у = 18, 2х + у = 9; у = 9 – 2х
Перебор:
1) х = 1; у = 7
2) х = 2; у = 5
3) х = 3; у = 3
4) х = 4; у = 1
5) х = 5; у = -1 < 0
6) х > 5; у < 0
Ответ: (1;7), (2;5), (3;3), (4;1)
Оглавление
Слайд 60Уравнение ах + bу = с имеет целые решения, если свободный
Решите уравнение 3х – 4у = 1 в целых числах.
3х = 4у + 1
Для целых решений левая часть должна делится на 3, следовательно, и правая часть делится на 3
Пусть у = 3р
Тогда 12р + 1 – не делится 3
Пусть у = 3р + 1
Тогда 12р + 4 + 1 – не делится 3
Пусть у = 3р + 2
Тогда 12р + 8 + 1 – делится 3
3х = 12р + 9
х = 4р + 3
12р + 9 – 4у – 1 = 1
12р + 9 – 4у = 1, 4у = 12р + 8
у = 3р + 2
Уравнение имеет бесконечное множество решений
Решение уравнений в целых числах
Оглавление
Слайд 61Формулы решения уравнения ax + bx = c
Заметим, что а
Решите уравнение 5х + 8у = 39 в целых числах.
1. Найдем подбором одно из решений
х = 1, 2 Нет целых решений.
х 0= 3 у0 = 3
2. Запишем по формулам решения:
5х + 8у = 39
х 0= 3
х =
3
- 8
p
y =
3
+ 5
p
у0 = 3
Оглавление
Слайд 62Решите уравнение -23х + 79у = 1 в целых числах.
Перебор для
Применим метод понижения коэффициентов.
23х - 79у = -1
Представим 79у как сумму чисел, одно из которых кратно 23
23х - 69у – 10у = -1
23х - 69у = 10у -1
Левая часть делится на 23, следовательно, правая тоже.
Подберем у так, чтобы 10у – 1 делилось бы на 23.
Очевидно, что у0 = 7
х0 = 24
х = 24 + 79р; у = 7 + 23р
Оглавление
Слайд 63Решение нелинейных уравнений
Метод разложения на множители
Состоит из разложения на
Задача 16. Решите уравнение ху + 2х + 3у =7 в целых числах.
Разложим левую часть:
ху + 2х + 3у + 6 – 6 = х(у + 2) + 3(у +2) – 6 = (у +2)(х +3) – 6
(у +2)(х +3) – 6 = 7, (у +2)(х +3) – 6 = 7
(у +2)(х +3) = 13
13 имеет множители ±1, ±13. При этом 13>0
Поэтому для решения в целых числах получим системы:
Оглавление
Слайд 64Метод решения уравнения относительно одной из переменных
Задача 17. Решите уравнение
Чтобы разложить на множители левую часть решим уравнение относительно х, считая у параметром.
х2 - 3ху + 2 у2 = 0
D = 9y2 – 8y2 = y2
(x – y)(x – 2y) = 0
Задача 18. Решите уравнение х2 - 3ху + 2 у2 = 11 в целых числах.
(x – y)(x – 2y) = 11
Далее см. задачу 16.
Оглавление
Слайд 65Задача 19. Решите уравнение 3(х2 + ху + у2) = х
Представим уравнение относительно одной из переменных либо х, либо у.
3х2 + (3у – 1)х + 3у2 – 8у = 0
D = (3y – 1)2 – 12(3y2 – 8y) = - 27y2 + 90y + 1
Уравнение имеет решения, если D ≥ 0
Решим: - 27y2 + 90y + 1 ≥ 0
27y2 - 90y – 1 = 0
у1 ≈ - 1, … у2 ≈ 2, …
-1 ≤ y ≤ 2
y = -1, 0, 1, 2
y = - 1
3х2 - 4х + 11 = 0 нет целых корней
y = 0
3х2 - х = 0 целое х = 0
y = 1
3х2 + 2х – 5 = 0 х = 1, х = 5/3
y = 2
3х2 + 5х – 4 = 0 нет целых корней
Ответ: (0;0), (1;1)
Оглавление
Слайд 66Задача 20. Решите уравнение x2 – xy + y2 = x
Будем решать относительно х: х2 – (1 + у)х + у2 – у = 0.
D = - 3y2 + 6y + 1
Чтобы корни были бы целыми, дискриминант должен быть полным квадратом.
Пусть – 3у2 + 6y + 1 = t2
Оценим t, выделив полный квадрат.
- 3((у2 – 2у + 1 – 1) +1 = - 3 (у – 1)2 + 4
- 3(у – 1)2 + 4 = t2
t2 ≤ 4, | t | ≤ 2, -2 ≤ t ≤ 2
t = - 2, - 1, 0, 1, 2
t = - 2
- 3(у – 1)2 + 4 = 4, y = 1
x2 – 2x = 0, x = 0, x = 2
t = - 1
- 3(у – 1)2 + 4 = 1, y = 2,
x2 – 3x + 2 = 0, x = 1, x = 2
t = 0
- 3(у – 1)2 + 4 = 0, нет целых решений
t = 1
См. t = - 1
у =0
x2 – x = 0, x = 0, x = 1
t = 2
См. t = - 2
Ответ: (0;1), (2;1), (1;2), (2;2), (0;0), (1;0)
Оглавление
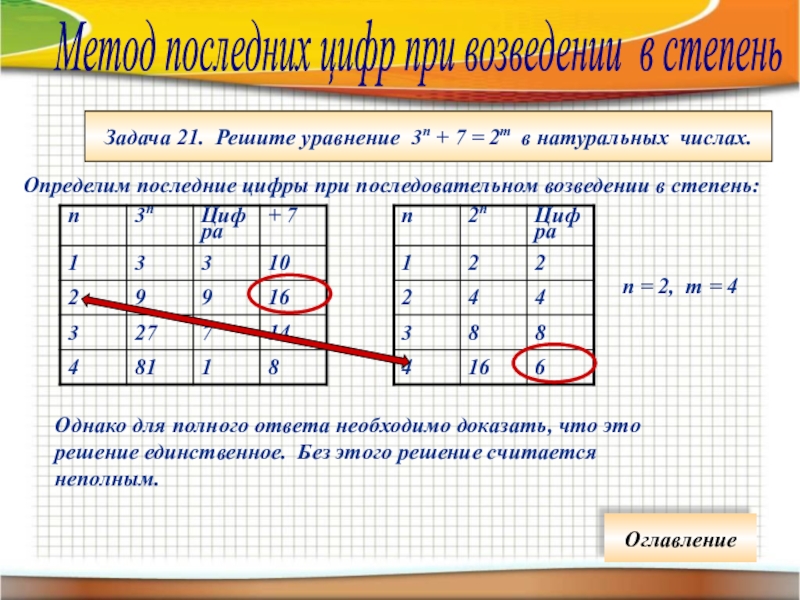
Слайд 67Метод последних цифр при возведении в степень
Задача 21. Решите уравнение
Определим последние цифры при последовательном возведении в степень:
n = 2, m = 4
Однако для полного ответа необходимо доказать, что это решение единственное. Без этого решение считается неполным.
Оглавление
Слайд 68Заметим, что периодичность последних цифр у 3п и 2т равна 4.
Рассмотрим
32 + 4k = 9 · 34k
24 + 4l = 16 · 24l
k=1, l=3
36 + 7 ≠ 216
k=2, l=1
310 + 7 ≠ 28
k=3, l=4
314 + 7 ≠ 220
k=4, l=2
318 + 7 ≠ 212
k=5, l=5
322 + 7 ≠ 224
Ни при каких k и l нельзя добиться равенства.
Ответ: п=2, т=4
Оглавление
Слайд 69
Метод оценок
Задача 22. Решите уравнение 2х2 – 5у2 = 3
Способ 1.
Заметим, что 2х2 – четное число (х – любое)
Так как 3 – нечетно, то 5у2 – нечетно, у – нечетно.
х = 2, у = 1
Больше решений нет: 2х2 > 5y2
Ответ: x = 2, y = 1
242 – 245 = - 3
Оглавление
Слайд 70Метод оценок
Задача 22. Решите уравнение 2х2 – 5у2 = 3
Способ 2.
Заметим, что 2х2 – четное число (х – любое)
Так как 3 – нечетно, то 5у2 – нечетно, у – нечетно.
2x2 – 5(2n + 1)2 = 3
2x2 – 20n2 - 20n - 5 = 3
2x2 = 20n2 + 20n + 8
x2 = 10n2 + 10n + 4
Так как х – натуральное, то 10n2 + 10n + 4 будет полным квадратом только если п = 0, то есть х2 = 4
х = 2
2· 4 – 5у2 = 3, у = 1
Ответ: x = 2, y = 1
Оглавление
Слайд 71Метод приведения к сумме положительных чисел
Задача 23. Решите уравнение х2
a2 + b2 > 0. Сумма положительных чисел – положительна.
Выделим полный квадрат относительно х:
х2 + 4ху + 4у2 – 4у2 + 13у2 = 58
(х + 2у)2 + 9у2 = 58
Так как сумма равна 58, то 9у2 < 58
у2 < 58/9
В целых числах | у | < 2
, y = ± 1, y = 0
у = 1, х2 + 4х + 13 = 58, х2 + 4х – 45 = 0, х = - 9, х = 5
Ответ: (5;1), (-5;-1), (9;-1), (-9;1)
При у = 0 целых х нет.
у = - 1, х2 - 4х + 13 = 58, х2 - 4х – 45 = 0, х = 9, х = - 5
Знак равно можно опустить, т.к. у будет нецелым числом
Оглавление
Слайд 72Принцип Дирихле
В несерьёзной форме принцип Дирихле гласит: «Нельзя посадить 7 кроликов
Не надо бояться дробного числа зайцев — если получается, что в ящике не меньше 7/3 зайцев, значит, их больше двух.
Более общая формулировка «Если z зайцев сидят в
k клетках, то найдётся клетка, в которой не менее z / k зайцев»
Оглавление
Оглавление
Слайд 73
Принцип Дирехле
«Нельзя посадить 7 кроликов в 3 клетки, чтобы
А как же я?
Не надо бояться дробного числа зайцев — если получается, что в ящике не меньше 7/3 зайцев, значит, их больше двух.
Оглавление
Слайд 74Принцип Дирехле
хотя бы в одной клетке
сидят, по крайней мере,
два
z
k
Если в k клетках
сидят z зайцев,
причем z > k, то
Нажмите на заслонку
Оглавление
Слайд 75Принцип Дирехле
хотя бы одна клетка
останется свободной.
Если в k клетках
сидят
причем z < k, то
Нажмите на каждую заслонку
Оглавление
Слайд 76Решение задач по принципу Дирехле
Таким образом, применяя данный метод, надо:
Определить,
Получить «клетки»; чаще всего «клеток» меньше (больше), чем «зайцев» на одну (или более).
Выбрать для решения требуемую формулировку принципа Дирихле.
k - клетки
z - зайцы
Оглавление
Слайд 771.В классе 15 учеников. Докажите, что найдутся, как минимум,
2 ученика, отмечающих
k - месяцы
z - ученики
k = 12
z = 15
2. В ковре размером 3 х 3 метра Коля проделал 8 дырок.
Докажите, что из него можно вырезать коврик размером 1 х 1 м,
не содержащий внутри себя дырок.
Решение.
Разрежем ковер на 9 ковриков размерами 1 х 1 м.
k - дырки
z - квадраты
k = 8
z = 9
Оглавление
Слайд 78
3. В 8 «Б» классе учится 27 школьников, знающих 109 песен.
k – количество песен
z - школьники
k = 4
z = 27
4. В городе 15 школ. В них обучается 6015 школьников. В концертном зале городского Дворца культуры 400 мест. Доказать, что найдётся школа, ученики которой не поместятся в этот зал.
Число школьников из 15 школ, могущих размещаться в зале 15 · 400 = 6000
k – количество мест
z – всего школьников
k = 6000
z = 6015
Оглавление
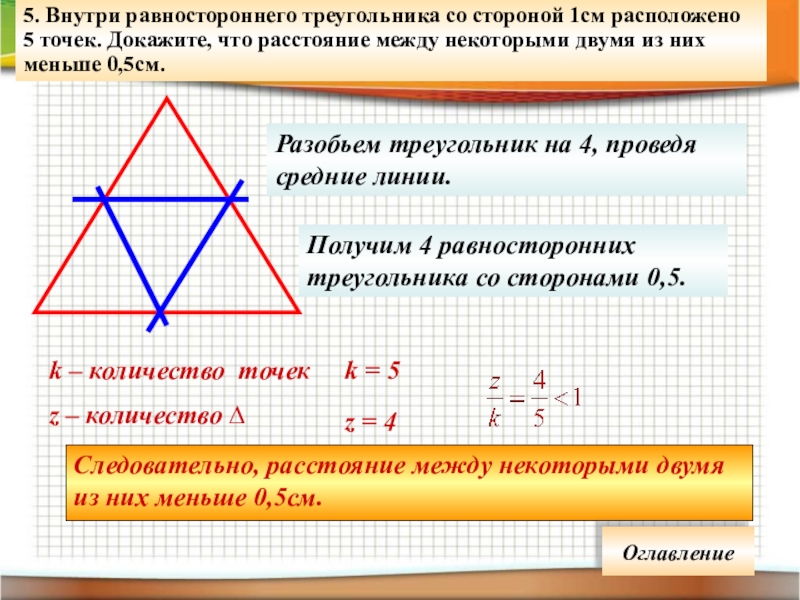
Слайд 795. Внутри равностороннего треугольника со стороной 1см расположено
5 точек. Докажите, что
Разобьем треугольник на 4, проведя средние линии.
Получим 4 равносторонних треугольника со сторонами 0,5.
k – количество точек
z – количество ∆
k = 5
z = 4
Оглавление
Слайд 80Последовательности
Числовая последовательность – это набор чисел, каждое из которых стоит
а1, а2, а3, …аn
а1 – первый член последовательности
аn – последний член последовательности
Арифметическая прогрессия
Арифметическая прогрессия – это последовательность, каждый член которой, начиная со второго, отличается от предыдущего на одно и тоже число.
аn - 1 – предыдущий член последовательности
аn + 1 – последующий член последовательности
d – разность прогрессии
аn = a1 + (n – 1)d
d = an – an - 1
Оглавление
Оглавление
Слайд 81Свойства арифметической прогрессии
аn = kn + b - линейная зависимость
Каждый член, начиная со второго, равен среднеарифметическому двух соседних членов
Оглавление
Слайд 82Геометрическая прогрессия
Геометрическая прогрессия – это последовательность, каждый член которой, начиная
q – знаменатель прогрессии
q = bn / bn - 1
Бесконечно убывающая геометрическая прогрессия – это прогрессия с |q| < 1
Оглавление
Слайд 83Свойства геометрической прогрессии
bn = kan - показательная зависимость от n
Каждый
Оглавление
Слайд 846. Доказать, что среди разных шести целых чисел найдутся два числа,
По признаку деления на число должно оканчиваться на 0 или 5
1. Разность двух чисел оканчивается на 0, если последние цифры равны.
Следовательно, если среди 6 чисел, есть числа, оканчивающиеся на одинаковую цифру, то разность будет делится на 5
2. Разность двух чисел оканчивается на 5, если имеются числа с последними цифрами, разность которых равна 5 .
|6 – 1| = 5
|7 – 2| = 5
|8 – 3| = 5
|9 – 4| = 5
3. Если последние цифры 0 и 5, разность делится на 5.
Следовательно, любой набор из 6 целых чисел содержит хотя бы пару чисел, соответствующую одному из 3 вариантов. Других нет.
Наименьшее количество пар равно 1
Оглавление
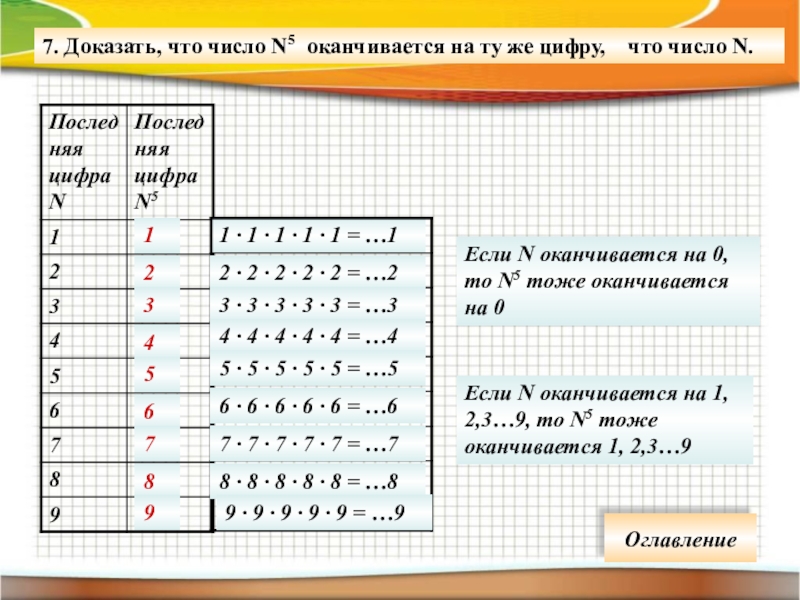
Слайд 857. Доказать, что число N5 оканчивается на ту же цифру,
1 · 1 · 1 · 1 · 1 = …1
2 · 2 · 2 · 2 · 2 = …2
3 · 3 · 3 · 3 · 3 = …3
4 · 4 · 4 · 4 · 4 = …4
5 · 5 · 5 · 5 · 5 = …5
6 · 6 · 6 · 6 · 6 = …6
7 · 7 · 7 · 7 · 7 = …7
8 · 8 · 8 · 8 · 8 = …8
9 · 9 · 9 · 9 · 9 = …9
1
2
3
4
5
6
7
8
9
Если N оканчивается на 0, то N5 тоже оканчивается на 0
Если N оканчивается на 1, 2,3…9, то N5 тоже оканчивается 1, 2,3…9
Оглавление
Слайд 868. В коробке лежат шарики 4-х разных цветов (много белых, много
k – цветов
z – количество вынутых шариков
k = 4
z = ?
Исходя из неравенства, наименьшее количество вынутых шариков 5
Оглавление
Слайд 879. Сколькими способами можно поставить на доску 8 белых шашек так, чтобы
Расставим по главной диагонали
Расставим по следующей диагонали
Расставим по следующей диагонали
Расставим по следующей диагонали
Всего 4 варианта и еще 4 по другой главной диагонали
Всего 8 способов.
Щелкните по каждой клетке диагонали.
Слайд 889. Сколькими способами можно поставить на доску 8 белых шашек так, чтобы
Аналитический способ
Будем расставлять шашки. В первом столбце мы можем поставить шашку в любую из 8 клеток.
Во втором столбце — в любую из 7 клеток. (Т. к. нельзя ставить в ту же строку, в которой стоит первая шашка.)
Аналогично в третьей строке мы можем поставить шашку в любую из 6 клеток, в четвёртой строке — в любую из пяти и т. д.
Всего 8 способов.
Оглавление
Слайд 8910. Сколькими способами можно поставить на доску 8 шашек разного цвета
Аналитический способ
Будем расставлять шашки. В первом столбце мы можем поставить шашку любого цвета в любую из 8 клеток. Всего 8·8 = 64
Во втором столбце — в любую из 7 клеток, любого цвета 7·8 = 56 < 64
Аналогично в третьей строке мы можем поставить шашку k.любого цвета, в любую из 6 клеток, в четвёртой строке — в любую из пяти и т. д.
Всего 82 = 64 способов.
Оглавление
Слайд 90
Решение логических задач
Пример 1. В симфонический оркестр приняли на работу
Смит самый высокий;
играющий на скрипке меньше ростом играющего на флейте;
играющие на скрипке и флейте и Браун любят пиццу;
когда между альтистом и трубачом возникает ссора, Смит мирит их;
Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
0
1
0
0
0
0
0
0
1
1
1
1
0
0
0
0
1
0
Оглавление
Слайд 91
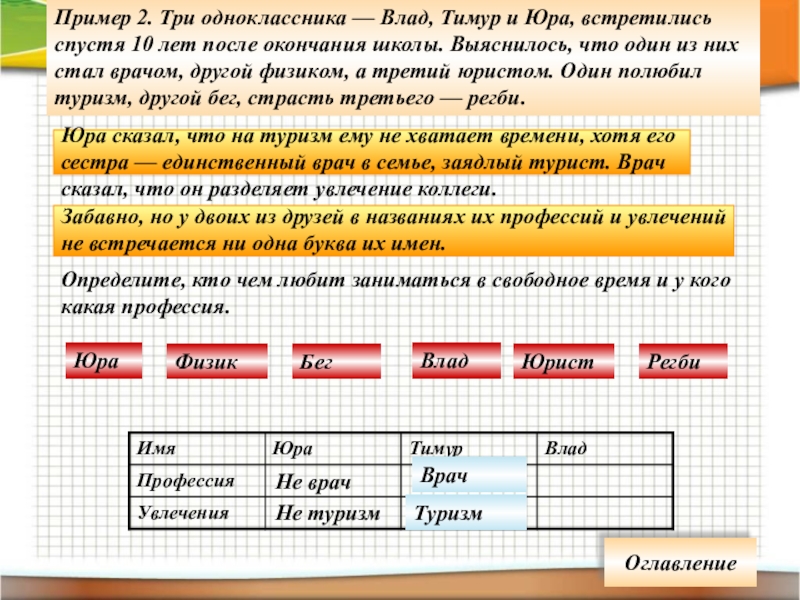
Пример 2. Три одноклассника — Влад, Тимур и Юра, встретились спустя
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Не врач
Не туризм
Юра
Физик
Бег
Влад
Юрист
Регби
Врач
Туризм
Оглавление
Слайд 92
Пример 5. Три дочери писательницы Дорис Кей — Джуди, Айрис и
Известно, что: Джуди живет не в Париже, а Линда — не в Риме;
парижанка не снимается в кино; та, кто живет в Риме, певица;
Линда равнодушна к балету.
Где живет Айрис, и какова ее профессия?
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
Это допущение
Оглавление
Слайд 93Пример 3. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский,
И так, имеем три утверждения. Правдиво только одно.
1. Вадим изучает китайский;
2. Сергей не изучает китайский;
3. Михаил не изучает арабский;
Пусть 1 утверждение верно, тогда 2 и 3 не верны
0
1
1
0
1
Получили противоречие.
Оглавление
Слайд 94Пример 3. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский,
И так, имеем три утверждения. Правдиво только одно.
1. Вадим изучает китайский;
2. Сергей не изучает китайский;
3. Михаил не изучает арабский;
Пусть 2 утверждение верно, тогда 1 и 3 не верны
0
1
1
0
1
Вадим – японский, Сергей – китайский, Михаил - арабский
Оглавление
Слайд 95Пример 3. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский,
И так, имеем три утверждения. Правдиво только одно.
1. Вадим изучает китайский;
2. Сергей не изучает китайский;
3. Михаил не изучает арабский;
Пусть 3 утверждение верно, тогда 1 и 2 не верны
1
1
0
1
Вадим – японский, Сергей – китайский, Михаил - арабский
Оглавление