- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Методы решения тригонометрических уравнений
Содержание
- 1. Презентация Методы решения тригонометрических уравнений
- 2. ВведениеТригонометрические уравнения возникают при решении задач по
- 3. Рекомендации по решению тригонометрических уравнений1. Если аргументы
- 4. IIII. Приведение к однородному уравнению первого порядкаII.
- 5. Решение уравнений разложением на множители
- 6. Пример 1 Решение:Ответ:
- 7. Решение уравнений, сводящихся к квадратным уравнениям
- 8. Пример 2Решение:Пусть , ответ:
- 9. Пример 3 Решение:Ответ:
- 10. Решение однородных и сводящихся к ним уравнений
- 11. Пример 4Решение:Т.к. значения x при которых cos3x
- 12. Пример 5 Решение: Уравнение является однородным второй степениответ:
- 13. Пример 6:Решение:В этом уравнении нельзя делить на cosxОтвет:
- 14. Решение уравнений с помощью введения вспомогательного аргумента
- 15. Пример 7 Решение:Ответ:
- 16. Решение уравнений преобразованием суммы тригонометрических функций в произведение
- 17. Пример 8Решение:Ответ:
- 18. Решение уравнений преобразования произведения тригонометрических функций в сумму
- 19. Пример 9Решение:Ответ:
- 20. Решение уравнений видаAsinx+Bcosx=Cгде A,B,C - действительные числа, A,B ≠0 Решается подстановкой
- 21. Пример 10Решение:Ответ:
- 22. Заключение. Изучение тригонометрических уравнений позволяет учащимся овладеть
- 23. БиблиографияАлексеев А. Тригонометрические подстановки. // Квант. –
Слайд 1Методы решения тригонометрических уравнений
(проектное задание)
Выполнила:
Остапенко Татьяна Ивановна, учитель математики и физики
МБОУ
Руководитель курса:
Вертелецкая О.В., старший преподаватель кафедры естественно-
математического образования
Слайд 2Введение
Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики
Цель работы: изучить методы решения тригонометрических уравнений, исследовать применение их к решению уравнений повышенной сложности и задач различного содержания.
Слайд 3Рекомендации по решению тригонометрических уравнений
1. Если аргументы функций одинаковые, попробовать получить
2. Если аргументы функций отличаются в два раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента.
3. Если аргументы функций отличаются в четыре раза, попробовать их привести к промежуточному двойному аргументу.
4. Если есть функции одного аргумента, степени свыше первой, попробовать понизить степень, используя формулы понижения степени или формулы сокращенного умножения.
5. Если есть сумма одноименных функций первой степени с разными аргументами (вне случаев 2,3), попробовать преобразовать сумму в произведение для появления общего множителя.
6. Если есть сумма разноимённых функций первой степени с разными аргументами (вне случаев 2, 3), попробовать использовать формулы приведения, получить затем случай 5.
7. Если в уравнении есть произведение косинусов (синусов) различных аргументов, попробовать свести его к формуле синус двойного аргумента, умножив и разделив это выражение на синус (косинус) подходящего аргумента:
8. Если в уравнении есть числовое слагаемое (множитель), то его можно представить в виде значений функции угла. Например:
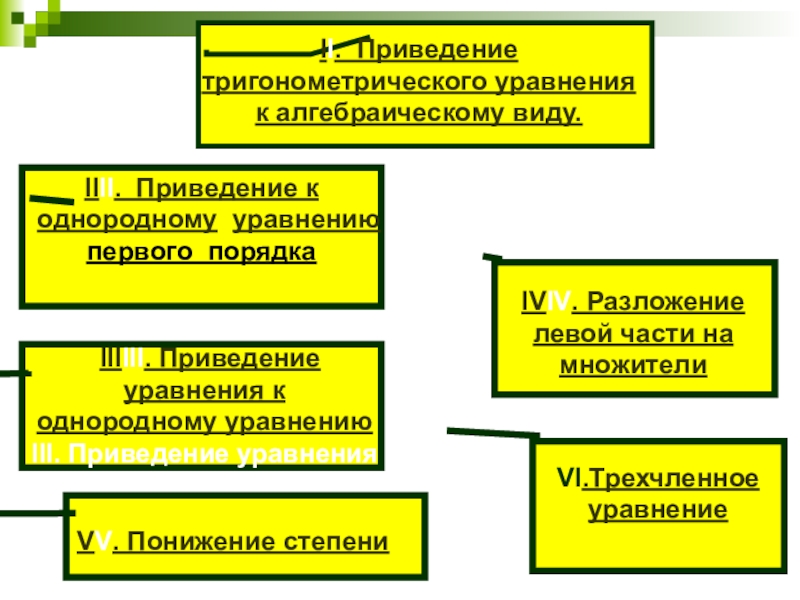
Слайд 4IIII. Приведение к однородному уравнению первого порядка
II. Приведение тригонометрического уравнения к
IIIIII. Приведение уравнения к однородному уравнению III. Приведение уравнения к однородному уравнению IIIII. Приведение уравнения к однородному уравнению II порядка
IVIV. Разложение левой части на множители
VV. Понижение степени
VI.Трехчленное уравнение
Слайд 11Пример 4
Решение:
Т.к. значения x при которых cos3x равен нулю, не являются
ответ:
Слайд 20Решение уравнений вида
Asinx+Bcosx=C
где A,B,C - действительные числа, A,B ≠0
Решается подстановкой
Слайд 22Заключение.
Изучение тригонометрических уравнений позволяет учащимся овладеть конкретными математическими знаниями, необходимыми
В данной работе рассмотрены основные методы решения тригонометрических уравнений, причем, как специфические, характерные только для тригонометрических уравнений, так и общие функциональные методы решения уравнений, применительно к тригонометрическим уравнениям.
Для успешного решения уравнений необходимо знать формулы корней простейших тригонометрических уравнений, значение тригонометрических функций для основных углов и значение обратных тригонометрических функций, универсальные правила решения уравнений. Рассмотрено решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим.
Приведенные методы не исчерпывают все многообразие способов решений тригонометрических уравнений. Однако рассмотренные типы уравнений встречаются наиболее часто и важно уметь распознавать в данном уравнении тот или иной тип.
Результаты данной работы могут быть использованы в качестве учебного материала при подготовке творческих работ, при составлении факультативных курсов для школьников, так же работа может применяться при подготовке учащихся к Единому государственному экзамену, вступительным экзаменам.
Слайд 23Библиография
Алексеев А. Тригонометрические подстановки. // Квант. – 1995. - №2. –с.
Выгодский М. Я. «Справочник по элементарной математике». М., «Наука», 1982 г.
Г. И. Глейзер История математики в школе. – М.: «Просвещение» 1983г.
Карасев В.А., Лёвшина Г.Д. «12 уроков по тригонометрии» - М.: Илекса, 2013.- 200 с.:ил.
Крамор В.С. Тригонометрические функции. – М.: Просвещение, 1979.
Сост. Гряда Н. Н. и др. Обобщающее повторение в системе подготовки к ЕГЭ по теме «Тригонометрические уравнения», Армавир, 2005г.
Цукарь А.Я. Упражнения практического характера по тригонометрии //Математика в школе. 1993-№3- с 12-15.
Шаталов В.Ф. Методические рекомендации для работы с опорными сигналами по тригонометрии. - М.: Новая школа, 1993.