- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Математика в архитектуре и искусстве
Содержание
- 1. Презентация Математика в архитектуре и искусстве
- 2. На определенном этапе своего развития
- 3. Термин “золотое сечение” принадлежит Леонардо да
- 4. Одной из самых известных фресок Леонардо
- 5. Как математика помогает добиться прочности сооружений.Люди с
- 6. Из всех видов искусств архитектура, пожалуй,
- 7. Египетская геометрия.Как известно они имеют форму правильных
- 8. Прочность сооружения обеспечивается не только материалом, из
- 9. С точки зрения геометрии она представляет собой
- 10. Гиперболоид.Следующим этапом развития архитектурных конструкций явилась каркасная
- 11. Однополостный гиперболоид На основе однополостных гиперболоидов была построена Шаболовская радиобашня
- 12. Однополостный гиперболоид – это поверхность, образованная вращением
- 13. Гиперболический параболоид.. Это поверхность, которая в сечении
- 14. Гиперболический параболоид Возможности гиперболических параболоидов открыл испанский
- 15. Парфенон является самым ярким примером
- 16. Что же такое «золотая пропорция»? «Золотая
- 17. Пропорции ПарфенонаСовременные архитекторы утверждают, что в основе
- 18. Слайд 18
- 19. Собор Парижской БогоматериСобор Парижской богоматери –
- 20. Храм Василия БлаженногоВ основе храма лежит золотое сечениеРяд золотого сечения:
- 21. Церковь Покрова на Нерли Несмотря на
- 22. Геометрические формы в разных архитектурных стилях.Геометрическая форма
- 23. В Спасской башне Московского кремля в основании
- 24. Симметрия – царица архитектурного совершенства.Соблюдение симметрии является
- 25. ЦилиндрЦилиндр - это тело, полученное при вращении прямоугольника вокруг прямой, содержащей его сторону.
- 26. Храм Геркулеса Построен во II в.
- 27. Пантеон «Храм всех богов» в
- 28. Темпьетто Отдельно стоящая часовня-ротонда, возведённая Донато Браманте
- 29. Справка.Дружественные числа – это два натуральных числа,
- 30. Это интересно!В настоящее время известно около 1100
- 31. Заключение Изучая математику мы часто обращаемся к
- 32. КонецЕдинство математики и искусства – важнейшее условие
Слайд 2 На определенном этапе своего развития человек начал задаваться вопросом:
Легко отыскать примеры прекрасного, но как трудно объяснить, почему они прекрасны. Платон.
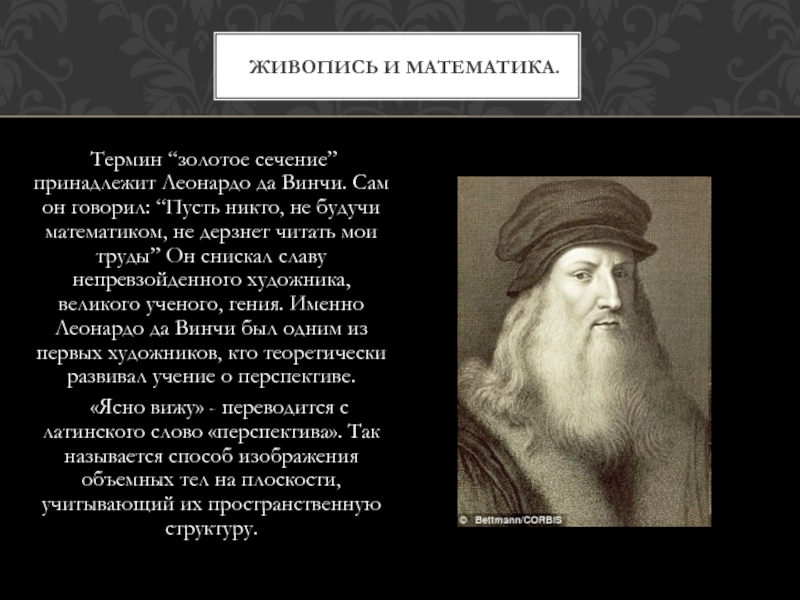
Слайд 3 Термин “золотое сечение” принадлежит Леонардо да Винчи. Сам он говорил:
«Ясно вижу» - переводится с латинского слово «перспектива». Так называется способ изображения объемных тел на плоскости, учитывающий их пространственную структуру.
Живопись и математика.
Слайд 4 Одной из самых известных фресок Леонардо да Винчи является «Тайная
Слайд 5Как математика помогает добиться прочности сооружений.
Люди с древних времен, возводя свои
На возведение зданий люди тратили огромные усилия и были заинтересованы в том, чтобы они простояли дольше. Благодаря этому, до наших дней дошли и древнегреческий Парфенон, и древнеримский Колизей.
Слайд 6 Из всех видов искусств архитектура, пожалуй, ближе всех к математике:
Конструкция древнеегипетской пирамиды является самой простой, прочной и устойчивой, её масса уменьшается по мере увеличения высоты над землёй. Форма пирамиды, подчёркнутая её огромными размерами, придаёт ей особую красоту и величие, вызывает ощущение вечности, бессмертия, мудрости и покоя.
Математика и архитектура
Слайд 7Египетская геометрия.
Как известно они имеют форму правильных четырехугольных пирамид.
Именно эта геометрическая
Самым прочным архитектурным сооружением с давних времен считаются египетские пирамиды.
Слайд 8 Прочность сооружения обеспечивается не только материалом, из которого оно создано, но
Математик бы сказал, что здесь очень важна геометрическая форма (тело), в которое вписывается сооружение.
Слайд 9С точки зрения геометрии она представляет собой многогранник, который получится, если
На смену пирамидам пришла стоечно-балочная система.
Слайд 10Гиперболоид.
Следующим этапом развития архитектурных конструкций явилась каркасная система.
Достаточно вспомнить конструкции
Слайд 11
Однополостный гиперболоид
На основе однополостных гиперболоидов была построена Шаболовская радиобашня
Слайд 12Однополостный гиперболоид – это поверхность, образованная вращением в пространстве гиперболы, расположенной
Любое осевое сечение однополостного гиперболоида будет ограничено двумя гиперболами.
Слайд 13Гиперболический параболоид.
. Это поверхность, которая в сечении имеет параболы и гиперболу.
Достаточно вспомнить американские небоскребы или, например, здание Кремлевского дворца съездов созданных из стекла и бетона.
Слайд 14Гиперболический параболоид
Возможности гиперболических параболоидов открыл испанский архитектор Феликс Кандела. Он показал
На фото изображён вечерний зал в Акапулько.
Слайд 15
Парфенон является самым ярким примером использования золотой пропорции в архитектуре.
Парфенон
Он был построен в дорическом ордере. Снаружи его украсили сценами жестоких битв. На западном фронтоне Парфенона был изображён миф о споре Афины и Посейдона. На главном (восточном) – рождение Афины
Слайд 16
Что же такое «золотая пропорция»?
«Золотая пропорция» - это понятие математическое, и
* Золотое сечение – это деление целого (точнее суммы) на две неравные части так, чтобы большая часть относилась к меньшей, как целое к большей.
Вводя обозначения: a – это большее или последнее число, x – среднее число (связь), y – меньшее (первое) число, в результате мы имеем: x : y = a : x, или y : x = x : a, или ay=x2.
Золотое сечение обозначается буквой Ф и равно 1,618033…
Слайд 17Пропорции Парфенона
Современные архитекторы утверждают, что в основе Парфенона лежит
Хэмбидж разбил фасад Парфенона на квадраты и прямоугольники, стороны которых относятся, как 1 к √5.
Легко видеть, что главные вертикальные размеры храма соотносятся в золотой пропорции (см. рисунок )
Жолтовский писал, что высоты поддерживающих (ВС) и поддерживаемых (АC) частей фасада соотносятся в золотой пропорции.
AC:BC=φ
Слайд 19Собор Парижской Богоматери
Собор Парижской богоматери – один из величайших памятников.
Огюст Шуази показал, что в основе пропорций фасада собора лежит квадрат, а высота башен равна радиусу окружности, вписанной в этот квадрат
Также на главном фасаде присутствует золотое сечение.
Слайд 21
Церковь Покрова на Нерли
Несмотря на простоту форм и лаконичность украшений, храм
Слайд 22Геометрические формы в разных архитектурных стилях.
Геометрическая форма сооружения настолько важна, что
Слайд 23В Спасской башне Московского кремля в основании можно увидеть прямой параллелепипед,
При более детальном рассмотрении и изучении деталей можно увидеть: круги – циферблаты курантов; шар – основание для крепления рубиновой звезды; полукруги – арки одного из рядов бойниц на фасаде башни и т.д..
Слайд 24Симметрия – царица архитектурного совершенства.
Соблюдение симметрии является первым правилом архитектора при
Если мы мысленно проведем вертикальную линию через шпиль на куполе и вершину фронтона, то увидит, что с двух сторон от нее абсолютно одинаковые части сооружения (колоннады и здания собора).
Слайд 25Цилиндр
Цилиндр - это тело, полученное при вращении прямоугольника вокруг прямой, содержащей
Слайд 26
Храм Геркулеса
Построен во II в. до н.э. в Риме на Бычьем
Слайд 27
Пантеон
«Храм всех богов» в Риме, памятник центрическо-купольной архитектуры Древнего Рима,
Слайд 28Темпьетто
Отдельно стоящая часовня-ротонда, возведённая Донато Браманте по заказу испанских монархов Фердинанда
Слайд 29Справка.
Дружественные числа – это два натуральных числа, для которых сумма всех
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284, 1 + 2 + 4 + 71 + 142 = 220
Числа Фибоначчи — элементы числовой последовательности1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи).
Золотое сечение или «божественное деление» - это такое деление целого на две неравные части, при котором большая часть AC так относится к целому AB, как меньшая BC к большей AC.
А С В
АС:АВ=СВ:АС
Например: 24:38=38:62
(приблизит. равно 0,6)
Слайд 30Это интересно!
В настоящее время известно около 1100 пар дружественных чисел. Например:
Компанейскими называется такая группа из k чисел, в которых сумма собственных делителей первого числа равна второму, сумма собственных делителей второго – третьему и т.д. А первое число равно сумме собственных делителей k-го числа(т.е.они последовательно дружественны). Пример пятёрки, пока единственной известной: 12496, 14288, 15472, 14536, 14264.
Отношение смежных чисел ряда Фибоначчи приближается к отношению золотого сечения. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618.Или 5:8=0,625,
а 8:13=0,615.
Слайд 31Заключение
Изучая математику мы часто обращаемся к истории. Это и понятно:
Чем дальше мы продвигаемся в изучении математики , тем больше узнаем не только интересного, но и мистического и загадочного .Вот, например, кроме дружественных и компанейских есть совершенные числа: каждое совершенное число дружественно себе( число 6).Следующим совершенным числом, известным древним, было "28". Они усматривали в этом числе особый смысл,
считая ,что Луна обновляется за 28 суток, потому что число "28" – совершенное.
Многие математики внесли свой исторический вклад в искусство и наоборот , люди искусства совершали математические открытия.