- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к внеклассному мероприятию Лист Мёбиуса
Содержание
- 1. Презентация к внеклассному мероприятию Лист Мёбиуса
- 2. Гипотеза«Лист Мёбиуса – удивительное и невероятное».Думаем, что
- 3. Цели работыВыяснить, что представляет собой лист МёбиусаВыяснить,
- 4. ЗадачиПознакомиться с литературой, в которой содержится информация
- 5. Предисловие Многие знают, что такое лента
- 6. Таинственный и знаменитый лист
- 7. Лист Мёбиуса – один
- 8. Рассказывают, что открыть свой «лист» Мёбиусу помогла служанка, сшившая однажды неправильно концы ленты.Легенда
- 9. Увлекательное исследование Запаситесь несколькими листами обычной белой бумаги, клеем и ножницами.
- 10. Берем бумажную ленту АВСD. Прикладываем
- 11. Получим такое перекрученное кольцо
- 12. ? Зададимся вопросом:
- 13. Красим, не отрываемся, на другую
- 14. Слайд 14
- 15. А вот что получилось у меняЛента перекручена два раза
- 16. Теперь сделайте новый лист Мёбиуса
- 17. А вот что получилось у меня
- 18. А если на три части? Три ленты? А ничего подобного! ?
- 19. Получим два сцепленных кольца. Одно
- 20. Человечек - перевертыш.
- 21. Он вернулся к месту старта.
- 22. Искусство и технологияМеждународный символ переработки представляет собой
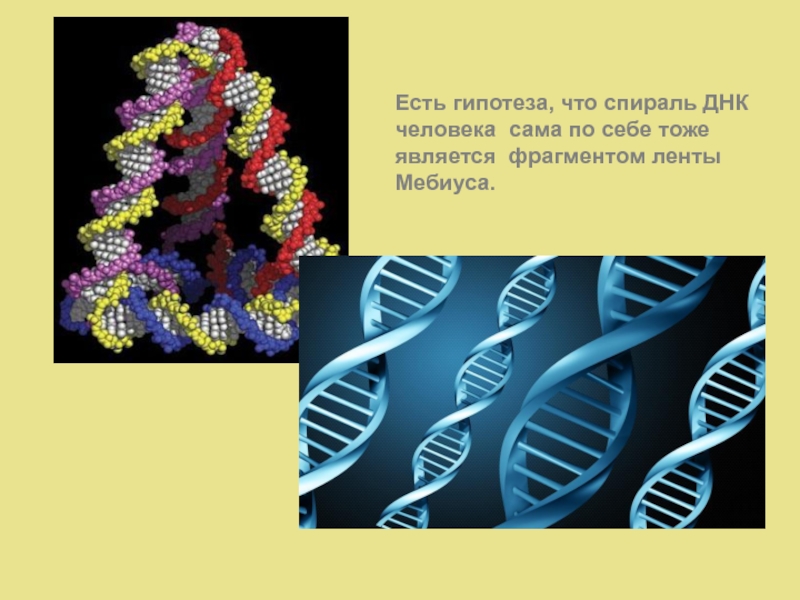
- 23. Есть гипотеза, что спираль ДНКчеловека сама по себе тоже является фрагментом ленты Мебиуса.
- 24. Невероятный проектновой библиотеки вАстане, Казахстан.
- 25. Лента Мёбиуса в скульптуре представлена в различных
- 26. Монумент у здания Президиума Национальной академии наукВ
- 27. В практике индийской йоги используется принцип движения
- 28. Заключение Считаем, что наша гипотеза подтвердилась и поставленные нами задачи выполнены.
- 29. Спасибо за внимание!Выполнили учащиеся МБОУ
Слайд 2Гипотеза
«Лист Мёбиуса – удивительное и невероятное».
Думаем, что изучение данной фигуры представляет
Хотим выяснить, могут ли удивительные свойства этой фигуры быть использованы в архитектуре и технике.
Слайд 3Цели работы
Выяснить, что представляет собой лист Мёбиуса
Выяснить, какие существуют типы листа
Познакомиться с удивительными свойствами листа Мёбиуса
Выяснить, где в жизни можно встретить лист Мёбиуса
Слайд 4Задачи
Познакомиться с литературой, в которой содержится информация о листе Мёбиуса
Проанализировать Интернет
Найти примеры использования листа Мёбиуса в жизни человека
Создать презентацию к работе
Слайд 5Предисловие
Многие знают, что такое лента (лист) Мёбиуса.
Слайд 6 Таинственный и знаменитый лист Мёбиуса (иногда говорят :
Слайд 7 Лист Мёбиуса – один из объектов области математики
Слайд 8 Рассказывают, что открыть свой «лист» Мёбиусу помогла служанка, сшившая однажды
Легенда
Слайд 9 Увлекательное исследование
Запаситесь несколькими листами обычной белой бумаги, клеем
Слайд 10 Берем бумажную ленту АВСD. Прикладываем ее концы АВ и
А
В
С
D
Слайд 12?
Зададимся вопросом:
сколько сторон у этого
у любого другого? А ничего подобного. У него ОДНА сторона. Не верите? Хотите – проверьте: попробуйте закрасить это кольцо с одной стороны.
Слайд 13 Красим, не отрываемся, на другую сторону не переходим. Красим...
Слайд 14 Теперь второй вопрос.
Что будет, если разрезать обычный лист бумаги? Конечно же, два обычных листа бумаги. Точнее, две половинки листа.
А что случится, если разрезать вдоль посередине это кольцо (это и есть лист Мёбиуса, или лента Мёбиуса) по всей длине? Два кольца половинной ширины? А ничего подобного. А что?
?
Слайд 16 Теперь сделайте новый лист Мёбиуса и скажите, что будет,
То же самое? А ничего подобного!
?
Слайд 19 Получим два сцепленных кольца. Одно из них вдвое
Слайд 20 Человечек - перевертыш.
Вырежьте бумажного человечка и
Слайд 21 Он вернулся к месту старта. Но в каком виде!
А чтобы он вернулся к старту в нормальном положении, ему нужно совершить ещё одно «круголистное » путешествие.
Проверьте!
Слайд 22Искусство и технология
Международный символ переработки
представляет собой Лист Мёбиуса.
Чудесные свойства ленты
породили множество научных трудов, изобретений, а также многочисленных фантастических рассказов.
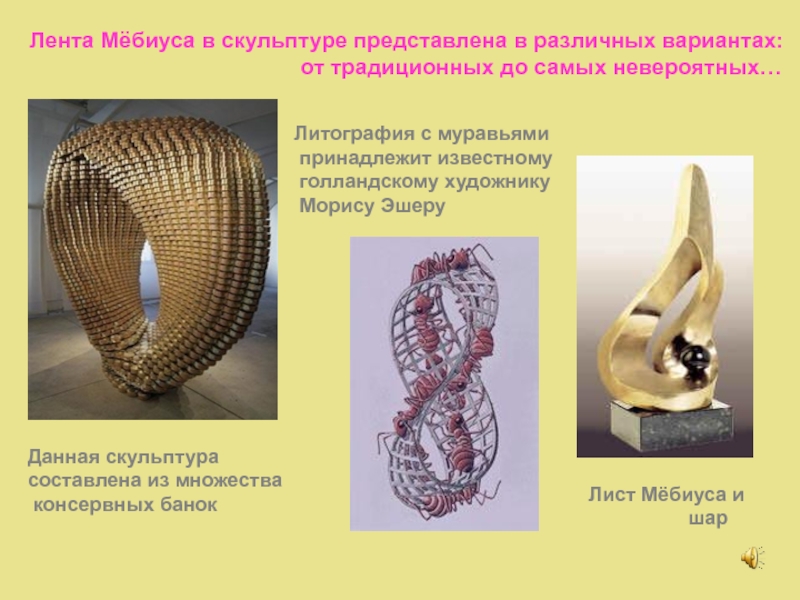
Слайд 25Лента Мёбиуса в скульптуре представлена в различных вариантах:
Данная скульптура
составлена из множества
консервных банок
Лист Мёбиуса и
шар
Литография с муравьями
принадлежит известному
голландскому художнику
Морису Эшеру
Слайд 26Монумент у здания Президиума Национальной академии наук
В Минске
Памятник ленте Мёбиуса
Слайд 27В практике индийской йоги
используется принцип движения
энергетических потоков по
траектории
Среди ювелирных изделий
также встречается
лента Мёбиуса.