- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по технологии РКМЧП
Содержание
- 1. Презентация к уроку по технологии РКМЧП
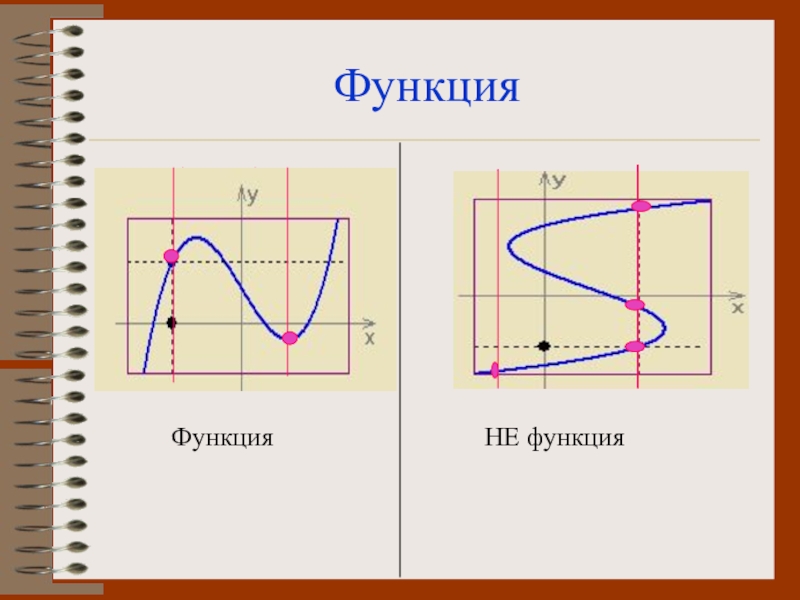
- 2. ФункцияФункция НЕ функция
- 3. уаб2Графики функций
- 4. Слайд 4
- 5. Возрастание и убывание функцииИду в гору. Функция возрастает на промежутке[b;a]Иду под гору. Функция убывает на промежутке[a;с]
- 6. Слайд 6
- 7. Слайд 7
- 8. Найдите производную функции:f(x)=3x³-2x²-3x+5f(x)=2x²+4x-4f(x)=sinxf(x)=sin2xf(x)=√xf(x)=2cosxf(x)=cosx+10
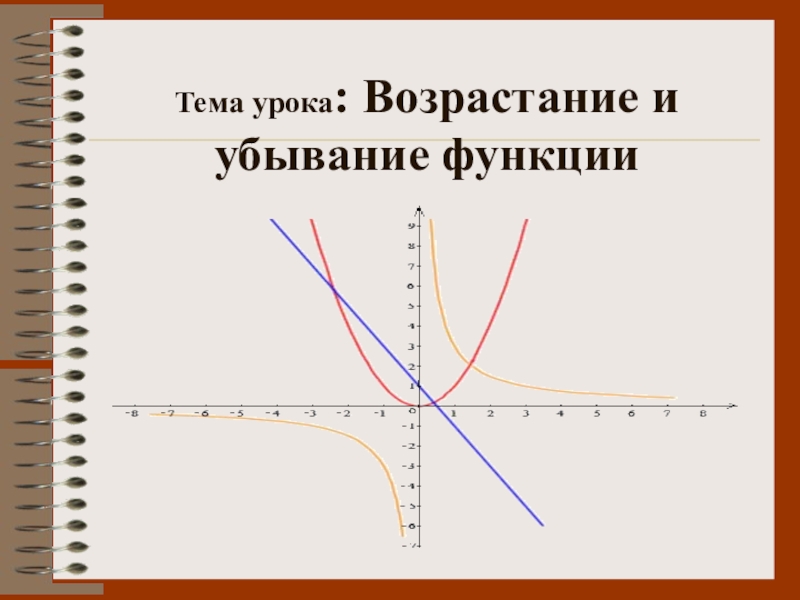
- 9. Тема урока: Возрастание и убывание функции
- 10. Цель урока: Ознакомление с признаками возрастания и
- 11. План урока1.Подумаем, что об этом мы уже
- 12. Слушаю – забываю.Смотрю – запоминаю.Делаю – понимаю.Конфуций
- 13. Минутка отдыхаСпал цветокСпал цветок (Закрыть глаза, расслабиться,
- 14. Слайд 14
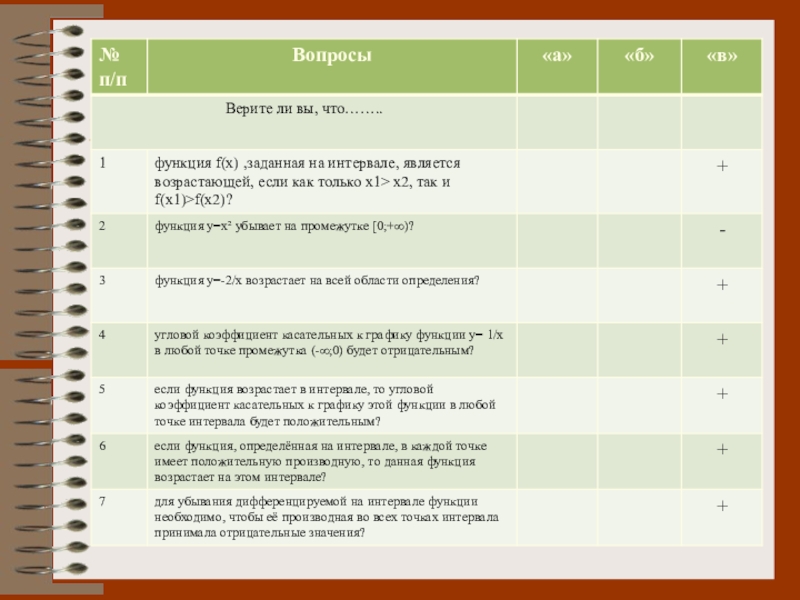
- 15. Проверь соседа!Вариант 1возрастает2. >3.критическимиВариант 2
- 16. f(x)=x³ - 6x² + 9x – 1f
- 17. Теорема: f(x) – непрерывна на I и
- 18. f(x) = x³ - 6x² + 9x
- 19. Ответ:f ´(x) > 0 ↔ f(x)↑, x
- 20. Проверь себя!f(x) = x³ + 3x² +
- 21. Ответ:f ´(x) > 0 ↔f(x)↑, x ϵ
- 22. Самостоятельная работаВАРИАНТ 1Найдите промежутки монотонности для функции f(x)=2х3-9х2-60х+25 ВАРИАНТ 2Найдите промежутки монотонности для функции f(x)=2х3-6х2-18х+75
- 23. Проверь себя!Вариант 1Ответ:f ´(x) > 0 ↔f(x)↑,
- 24. - обратиться к справочному материалу;- обратиться учебнику;-
- 25. Рефлексия Продолжите фразу(письменно или устно):«Сегодня на уроке
- 26. Вам от души желаю я,Друзья всего хорошего.А
- 27. Спасибо за урок!-)
ФункцияФункция НЕ функция
Слайд 5Возрастание и убывание функции
Иду в гору. Функция возрастает на промежутке[b;a]
Иду под
гору. Функция убывает на промежутке[a;с]
![Возрастание и убывание функцииИду в гору. Функция возрастает на промежутке[b;a]Иду под гору. Функция убывает на промежутке[a;с]](/img/thumbs/7d06b0bbac5b118275b7aee3dec79f21-800x.jpg "Презентация к уроку по технологии РКМЧП Возрастание и убывание функцииИду в гору. Функция возрастает на промежутке[b;a]Иду под гору. Функция убывает на промежутке[a;с]")
Слайд 8Найдите производную функции:
f(x)=3x³-2x²-3x+5
f(x)=2x²+4x-4
f(x)=sinx
f(x)=sin2x
f(x)=√x
f(x)=2cosx
f(x)=cosx+10
Слайд 10Цель урока: Ознакомление с признаками возрастания и убывания функции, алгоритмом исследования
функции на промежутки монотонности; достаточным условием возрастания и убывания функции.
Слайд 11План урока
1.Подумаем, что об этом мы уже знаем или предполагаем.
2.Вдумчиво прочитаем
текст.
3.Снова вернёмся к вопросам, рассмотренным в начале урока и обсудим-правы ли мы были, а если нет, то в чём ошиблись.
4.Закрепим полученные знания на практике.
5.Подведём итог урока.
3.Снова вернёмся к вопросам, рассмотренным в начале урока и обсудим-правы ли мы были, а если нет, то в чём ошиблись.
4.Закрепим полученные знания на практике.
5.Подведём итог урока.
Слайд 13Минутка отдыха
Спал цветок
Спал цветок
(Закрыть глаза, расслабиться, помассировать веки,
слегка надавливая
на них по часовой стрелке и против нее.)
И вдруг проснулся,
(Поморгать глазами.)
Больше спать не захотел,
(Руки поднять вверх (вдох). Посмотреть на руки.)
Встрепенулся, потянулся,
(Руки согнуты в стороны (выдох)
Взвился вверх и полетел.
(Потрясти кистями, посмотреть вправо-влево.)
И вдруг проснулся,
(Поморгать глазами.)
Больше спать не захотел,
(Руки поднять вверх (вдох). Посмотреть на руки.)
Встрепенулся, потянулся,
(Руки согнуты в стороны (выдох)
Взвился вверх и полетел.
(Потрясти кистями, посмотреть вправо-влево.)
Слайд 16f(x)=x³ - 6x² + 9x – 1
f ´(x) = 3x² -
12x + 9
Найдем критические точки:
f ´(x) = 0, 3x² - 12x + 9 = 0
x² - 4x + 3 = 0
x = 1 и х = 3
Найдем критические точки:
f ´(x) = 0, 3x² - 12x + 9 = 0
x² - 4x + 3 = 0
x = 1 и х = 3
х
1
3
Слайд 17Теорема: f(x) – непрерывна на I и имеет f ´(x)
а)
f ´(x) > 0, то f(x) – возрастает
б) f ´(x) ˂ 0, то f(x) – убывает
в) f ´(x) = 0, то f(x) – постоянна(константа)
б) f ´(x) ˂ 0, то f(x) – убывает
в) f ´(x) = 0, то f(x) – постоянна(константа)
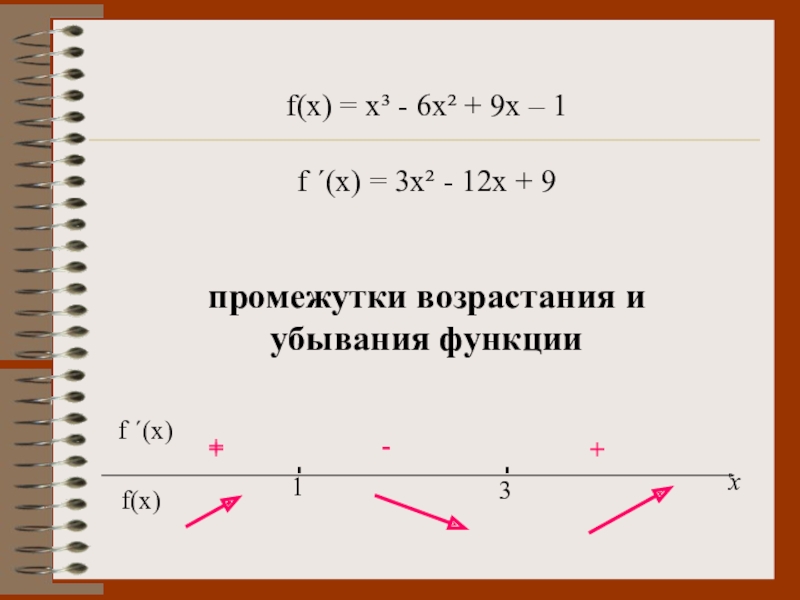
Слайд 18f(x) = x³ - 6x² + 9x – 1
f ´(x) =
3x² - 12x + 9
промежутки возрастания и убывания функции
промежутки возрастания и убывания функции
х
f ´(x)
f(x)
1
3
+
-
+
+
Слайд 20Проверь себя!
f(x) = x³ + 3x² + 24x + 1
1.х ϵ
R
2. f ´(x) = 3x² +6x -24
3. Найдем критические точки:
f ´(x) =0, 3x² +6x -24=0
x² + 2x - 8 = 0
x = 2 и х =-4
4. промежутки возрастания и убывания функции
-4 2
2. f ´(x) = 3x² +6x -24
3. Найдем критические точки:
f ´(x) =0, 3x² +6x -24=0
x² + 2x - 8 = 0
x = 2 и х =-4
4. промежутки возрастания и убывания функции
-4 2
f ´(x)
f(x)
х
+
-
+
Слайд 22
Самостоятельная работа
ВАРИАНТ 1
Найдите промежутки монотонности для функции f(x)=2х3-9х2-60х+25
ВАРИАНТ 2
Найдите промежутки
монотонности для функции f(x)=2х3-6х2-18х+75
Слайд 23Проверь себя!
Вариант 1
Ответ:
f ´(x) > 0 ↔f(x)↑,
x ϵ (-∞; -2)
и (5; + ∞)
f ´(x) ˂ 0 ↔ f(x)↓,
х ϵ(-2;5)
f ´(x) ˂ 0 ↔ f(x)↓,
х ϵ(-2;5)
Вариант 2
Ответ:
f ´(x) > 0 ↔f(x)↑,
x ϵ (-∞; -1) и (3; + ∞)
f ´(x) ˂ 0 ↔ f(x)↓,
х ϵ(-1;3)
Слайд 24- обратиться к справочному материалу;
- обратиться учебнику;
- проанализировать выполнение аналогичных заданий;
-
составить собственные примеры;
- обратиться за помощью к учителю.
- обратиться за помощью к учителю.
План действий по локализации индивидуальных затруднений
Слайд 25Рефлексия
Продолжите фразу
(письменно или устно):
«Сегодня на уроке я узнал…»
«Сегодня на уроке
я научился…»
«Сегодня на уроке я познакомился…»
«Сегодня на уроке я повторил…»
«Сегодня на уроке я закрепил…»
«Сегодня на уроке я познакомился…»
«Сегодня на уроке я повторил…»
«Сегодня на уроке я закрепил…»
Слайд 26Вам от души желаю я,
Друзья всего хорошего.
А всё хорошее, друзья,
Даётся нам
недёшево.
С.Маршак
С.Маршак
