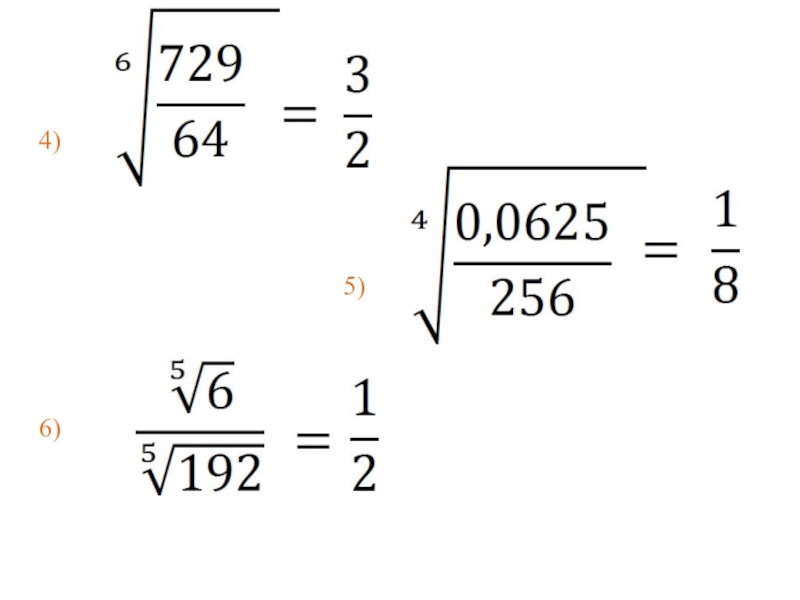аппетитом»
Анатоль Франс
(1844-1924)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку на тему Свойства корня n-ой степени
Содержание
- 1. Презентация к уроку на тему Свойства корня n-ой степени
- 2. Тема урока Свойства корня n-ой степени
- 3. КАТЕХИЗИС
- 4. продолжить формулировку1.Корень n-степени (n=2,3,4,5, …) из произведения
- 5. 2. Если a≥ 0, b>0 и n=2,3,4,5,… то справедливо равенство =Пример: ==
- 6. 3. Если a≥ 0, n=2,3,4,5,…
- 7. 4. Если a≥ 0, n
- 8. 5. Если показатели корня и подкоренного выражения
- 9. «Любое правило хорошо тем, что если с
- 10. Найдите значение числового выражения 1,522)
- 11. 4)
- 12. сравните2)
- 13. Задания открытого банка задач
- 14. Решение. Задания открытого банка задачРешение.
- 15. ? – мне есть над чем работать
- 16. «Вы - талантливые дети! Когда – нибудь
Тема урока Свойства корня n-ой степени
Слайд 4продолжить формулировку
1.Корень n-степени (n=2,3,4,5, …) из произведения двух неотрицательных чисел равен…
произведению корней n-степени из этих чисел:
=
Пример:
=
=
2·3=6
Слайд 85. Если показатели корня и подкоренного выражения умножить или разделить на
одно и то же натуральное число, то…
значение корня не изменится
Пример:
Слайд 9«Любое правило хорошо тем, что если с самого начала мы можем
предвидеть и впоследствии подтвердить его, то, следуя этому, мы достигнем цели»
Вильгельм Лейбниц
Слайд 16«Вы - талантливые дети! Когда – нибудь вы сами приятно поразитесь,
какие вы умные, как много вы сумеете, если будете постоянно работать над собой…»
Жан-Жак Руссо
