- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики по теме: Решение простейших тригонометрических уравнений
Содержание
- 1. Презентация к уроку математики по теме: Решение простейших тригонометрических уравнений
- 2. I Этап: Готовимся к ЕГЭКлассная работа 19.12.12
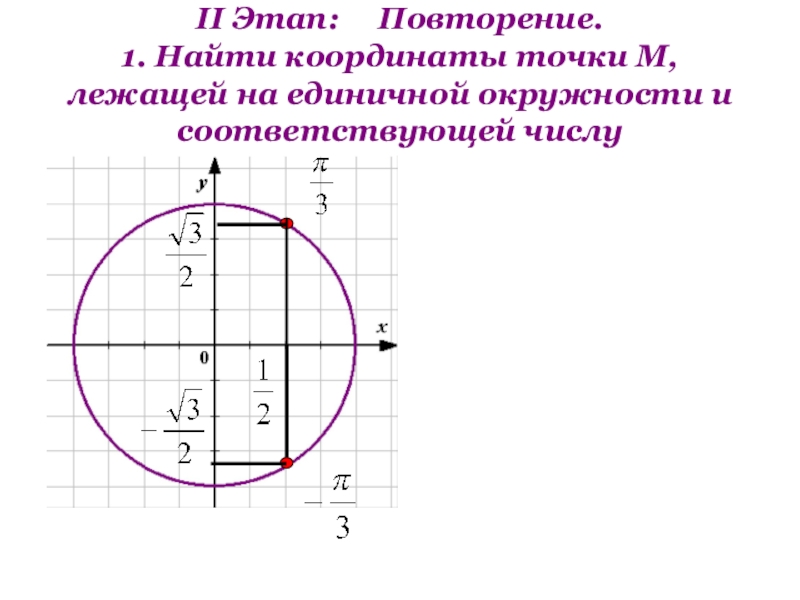
- 3. II Этап: Повторение. 1. Найти
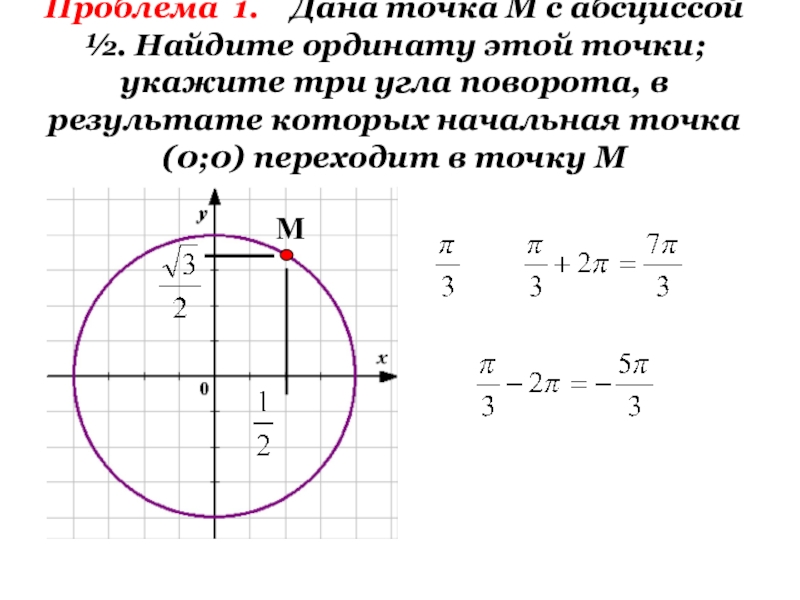
- 4. Проблема 1. Дана точка М с
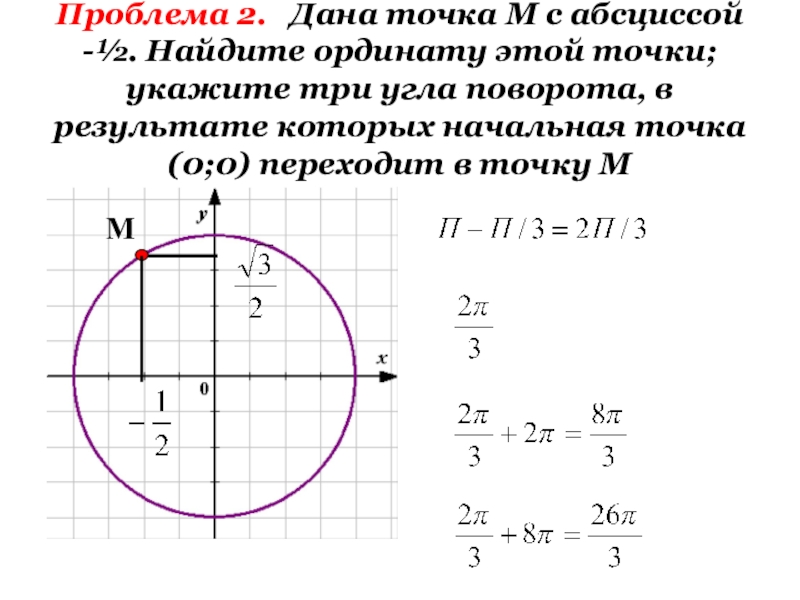
- 5. Проблема 2. Дана точка М с
- 6. π0arccos аАрккосинусом числа а называют такое число
- 7. III Этап: Актуализация опорных знаний. 1) Имеет
- 8. Вычислить
- 9. Решение простейших тригонометрических уравнений.
- 10. *2) уметь определять значения синуса, косинуса, тангенса
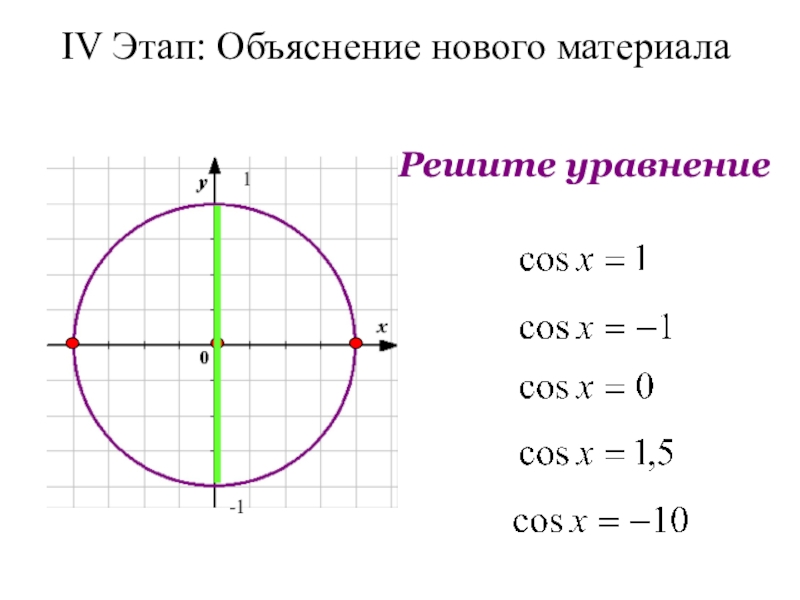
- 11. Решите уравнение1-1IV Этап: Объяснение нового материала
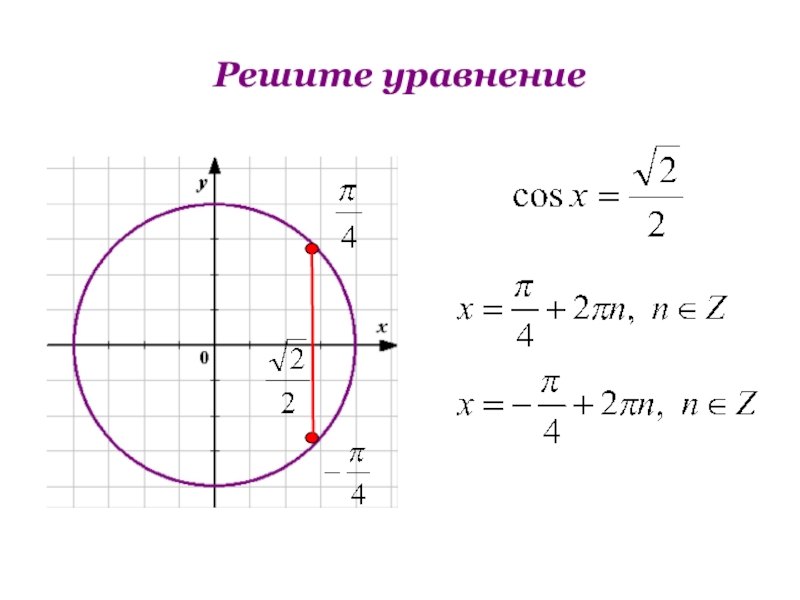
- 12. Решите уравнение
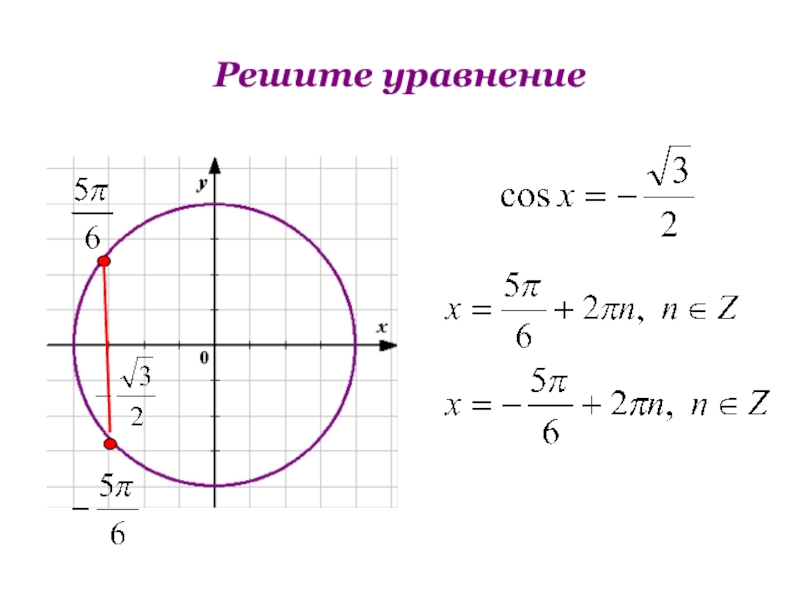
- 13. Решите уравнение
- 14. Решим при помощичисловой окружностиуравнение cos х =
- 15. Решим при помощичисловой окружностиуравнение cos х =
- 16. Решим при помощичисловой окружностиуравнение cos х =
- 17. Решим при помощичисловой окружностиуравнение cos х =
- 18. Уравнение cos х = a называется
- 19. Подводим итогиcos x = a
- 20. VI Этап: Решение уравнений соs х =a. Сколько серий решений имеет уравнение:
- 21. VII Этап: Закрепление. Самостоятельная работаВариант 1Вариант 21. Вычислить2. Решить уравнение
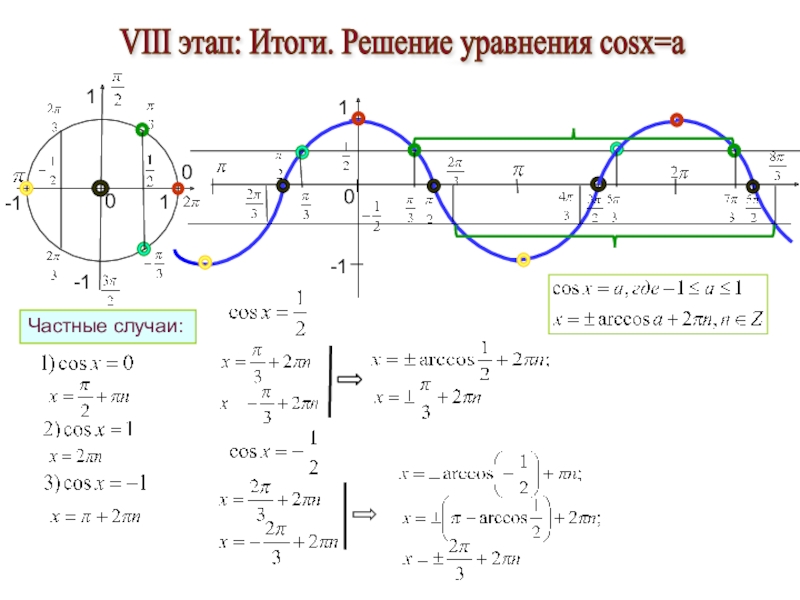
- 22. VIII этап: Итоги. Решение уравнения cosx=a 1-10001-1-11Частные случаи:
- 23. Слайд 23
- 24. Домашнее задание.
Слайд 3II Этап: Повторение. 1. Найти координаты точки М, лежащей на
Слайд 4Проблема 1. Дана точка М с абсциссой ½. Найдите ординату
М
Слайд 5Проблема 2. Дана точка М с абсциссой -½. Найдите ординату
М
Слайд 6π
0
arccos а
Арккосинусом числа а называют такое число из промежутка
[0;π
а
arccos (-a)= π -arccos a
-а
π-arccos a
Арккосинус.
Слайд 7III Этап: Актуализация опорных знаний.
1) Имеет ли смысл выражение
2) Может
3) Вычислите
Слайд 9
Решение простейших тригонометрических уравнений.
Цель: приложить усилия, чтобы понять как решаются простейшие
Слайд 10*
2) уметь определять значения синуса, косинуса,
тангенса и котангенса для точек
окружности;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.
1) уметь отмечать точки на числовой
окружности;
3) знать свойства основных
тригонометрических функций;
Чтобы успешно решать простейшие
тригонометрические уравнения нужно
Слайд 14Решим при помощи
числовой окружности
уравнение cos х = a.
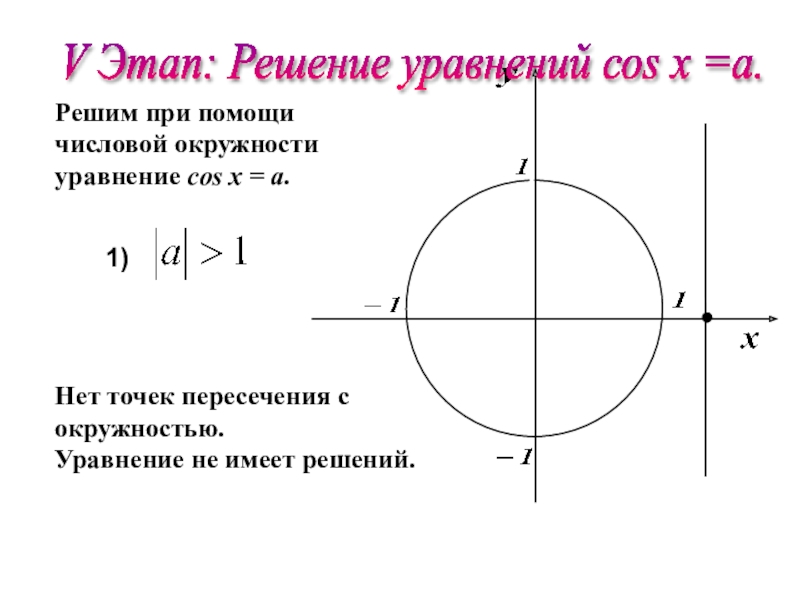
1)
Нет точек пересечения
Уравнение не имеет решений.
V Этап: Решение уравнений соs х =a.
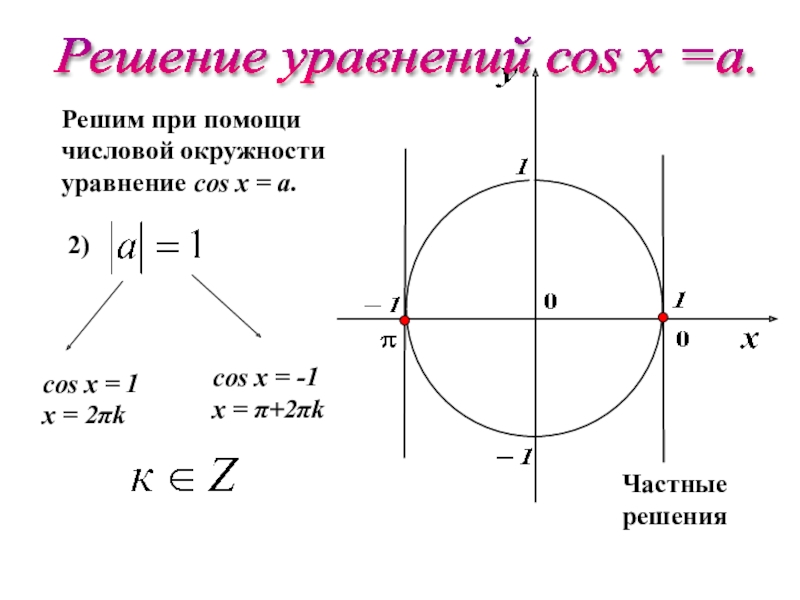
Слайд 15Решим при помощи
числовой окружности
уравнение cos х = a.
2)
cos х = 1
х
cos х = -1
х = π+2πk
Частные решения
Решение уравнений соs х =a.
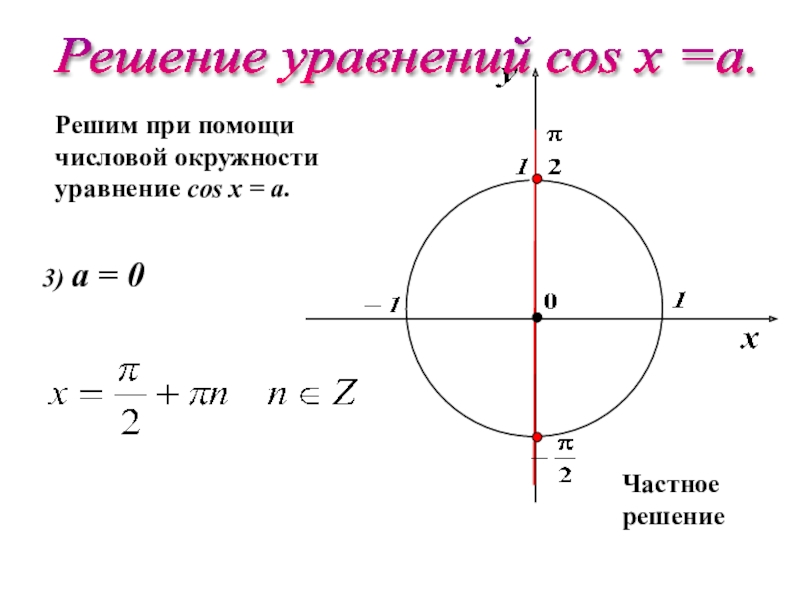
Слайд 16Решим при помощи
числовой окружности
уравнение cos х = a.
3) а = 0
Частное
Решение уравнений соs х =a.
Слайд 17Решим при помощи
числовой окружности
уравнение cos х = a.
4)
Общее решение
arccos а
-arccos
Корни, симметричные относительно Оx могут быть записаны:
х = ± arccos a+2πk
или
а
Решение уравнений соs х =a.
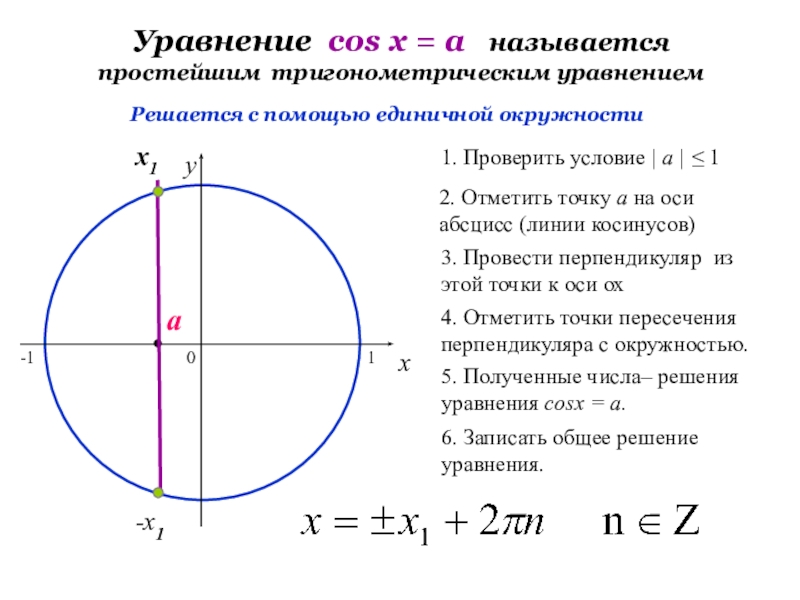
Слайд 18Уравнение cos х = a называется простейшим тригонометрическим уравнением
0
x
y
2. Отметить
3. Провести перпендикуляр из этой точки к оси ох
4. Отметить точки пересечения перпендикуляра с окружностью.
5. Полученные числа– решения уравнения cosх = a.
6. Записать общее решение уравнения.
1. Проверить условие | a | ≤ 1
a
х1
-х1
-1
1
Решается с помощью единичной окружности


![Презентация к уроку математики по теме: Решение простейших тригонометрических уравнений π0arccos аАрккосинусом числа а называют такое число из промежутка [0;π ], π0arccos аАрккосинусом числа а называют такое число из промежутка [0;π ], косинус которого равен ааarccos (-a)= π](/img/thumbs/43213b4bf18b2508259384f708f358de-800x.jpg)