Салтыкова Руслана Алусьевна
Учитель математики
МБОУ СОШ д. Новая Бура
2016 г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к статье Квадрат Пирсона в задачах на смеси из двух и трех растворов (сплавов)
Содержание
- 1. Презентация к статье Квадрат Пирсона в задачах на смеси из двух и трех растворов (сплавов)
- 2. Квадрат Пирсона (метод креста или конверт Пирсона)Карл
- 3. В сосуд, содержащий 5 литров 12-процентного водного
- 4. Смешали некоторое количество 15-процентного раствора некоторого вещества
- 5. Смешали 4 литра 15-процентного водного раствора некоторого
- 6. Имеется два сплава. Первый содержит 10% никеля,
- 7. Имеется два сплава. Первый сплав содержит
- 8. Смешав 30-процентный и 60-процентный растворы кислоты
- 9. Имеется два сосуда. Первый содержит 30
- 10. Свежие грибы содержат 90% воды, а
- 11. Изюм получается в процессе сушки винограда.
- 12. Имеется два сплава с разным содержанием
Слайд 1Республика Башкортостан
Краснокамский район
Квадрат Пирсона
в задачах на смеси
из двух и
Слайд 2Квадрат Пирсона
(метод креста или конверт Пирсона)
Карл (Чарльз) Пирсон (1857-1936 гг.)
«Квадрат Пирсона» – это механический способ, который позволяет рационально и экономно проводить вычисления при решении задач на концентрацию.
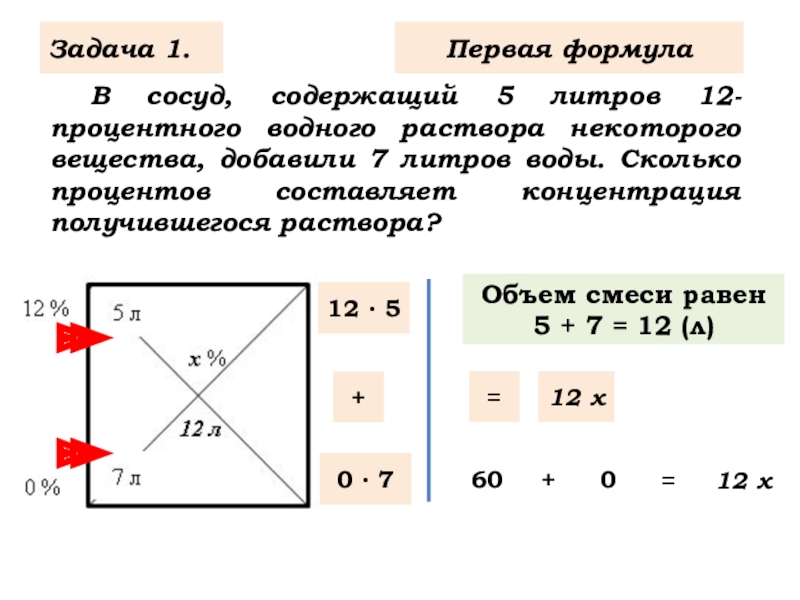
Слайд 3 В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили
Задача 1.
Объем смеси равен
5 + 7 = 12 (л)
12 ∙ 5
0 ∙ 7
+
60
+
0
=
12 х
12 х
=
Первая формула
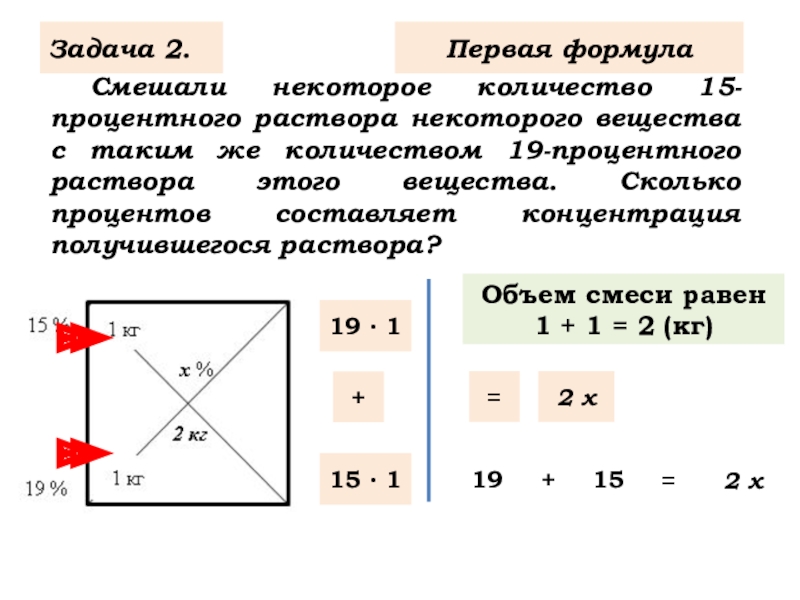
Слайд 4 Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством
Задача 2.
Объем смеси равен
1 + 1 = 2 (кг)
19 ∙ 1
15 ∙ 1
+
19
+
15
=
2 х
2 х
=
Первая формула
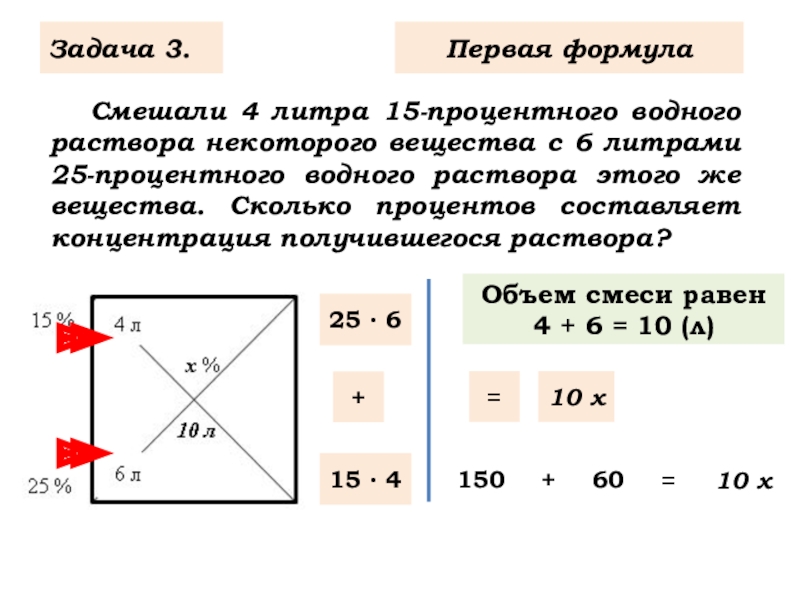
Слайд 5 Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами
Задача 3.
Объем смеси равен
4 + 6 = 10 (л)
25 ∙ 6
15 ∙ 4
+
150
+
60
=
10 х
10 х
=
Первая формула
Слайд 6 Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля.
Задача 4.
30 ∙ (200 – х)
10 ∙ х
+
30 ∙ (200 – х)
+
10 х
=
5000
25 ∙ 200
=
Первая формула
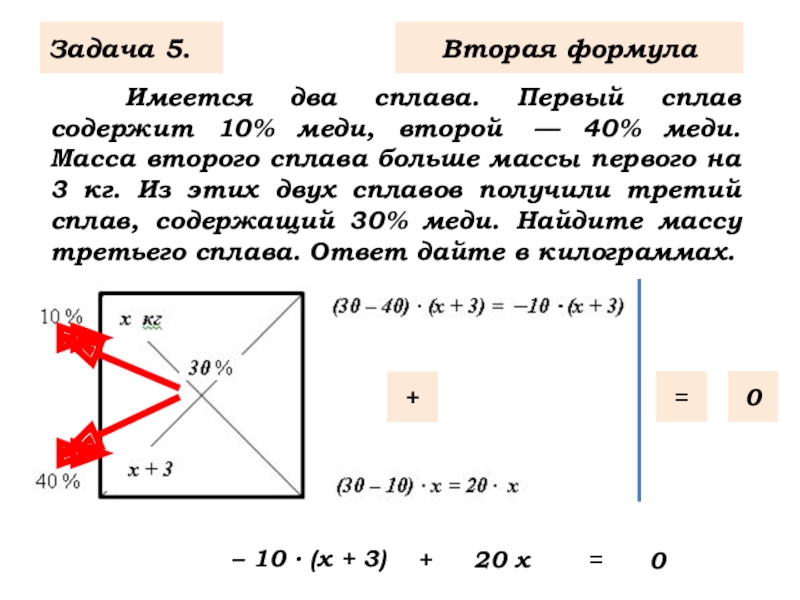
Слайд 7 Имеется два сплава. Первый сплав содержит 10% меди, второй —
Задача 5.
+
– 10 ∙ (х + 3)
+
20 х
=
0
0
=
Вторая формула
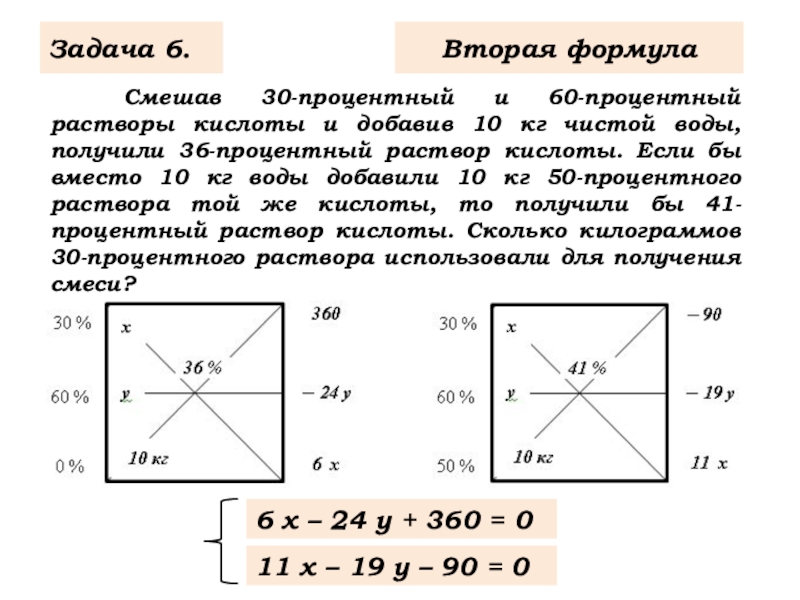
Слайд 8 Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг
Задача 6.
6 х – 24 y + 360 = 0
Вторая формула
11 х – 19 y – 90 = 0
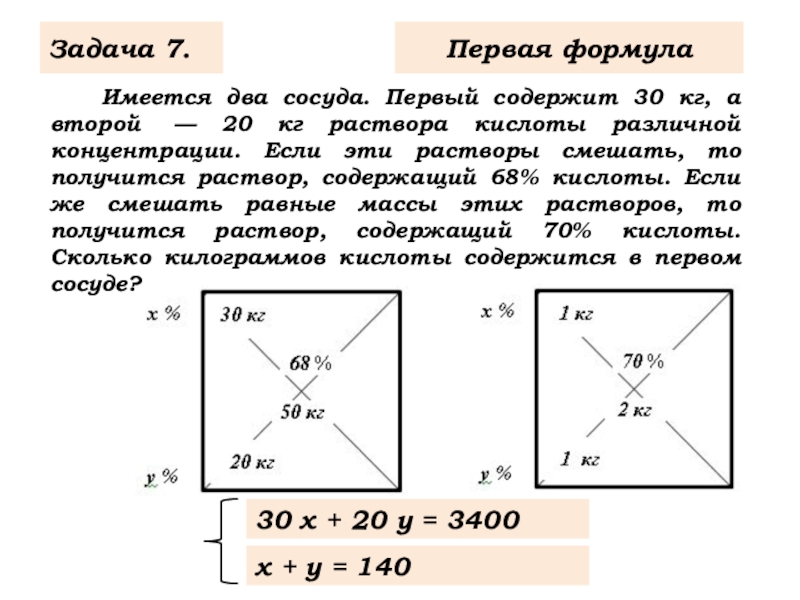
Слайд 9 Имеется два сосуда. Первый содержит 30 кг, а второй —
Задача 7.
30 х + 20 y = 3400
Первая формула
х + y = 140
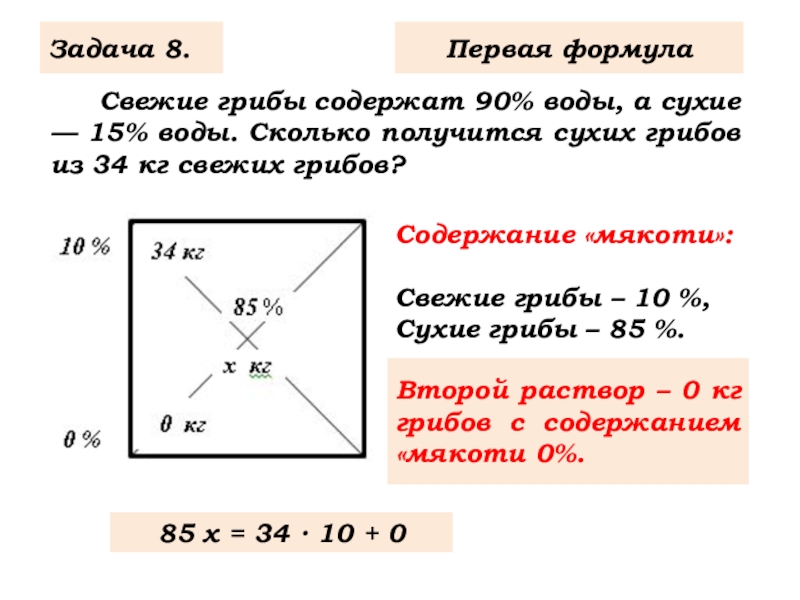
Слайд 10 Свежие грибы содержат 90% воды, а сухие — 15% воды.
Задача 8.
Первая формула
Содержание «мякоти»:
Свежие грибы – 10 %,
Сухие грибы – 85 %.
Второй раствор – 0 кг грибов с содержанием «мякоти 0%.
85 х = 34 ∙ 10 + 0
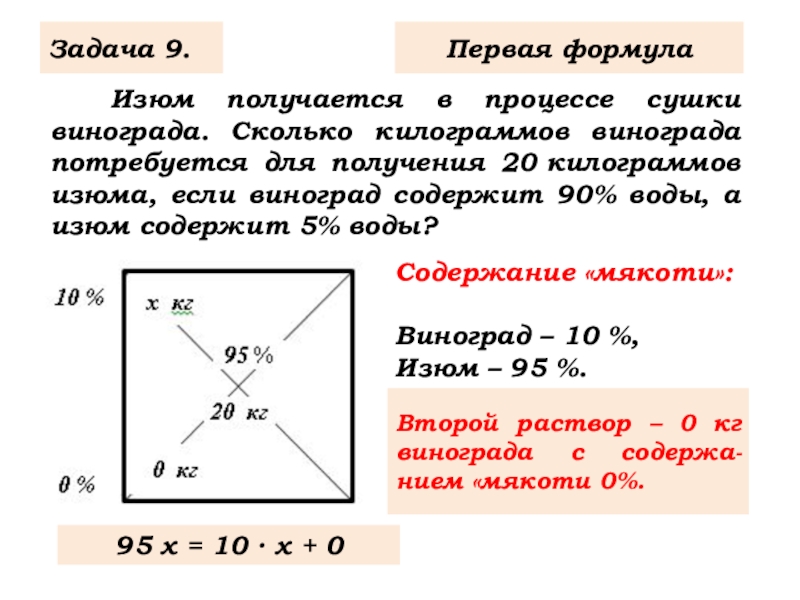
Слайд 11 Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется
Задача 9.
Первая формула
Содержание «мякоти»:
Виноград – 10 %,
Изюм – 95 %.
Второй раствор – 0 кг винограда с содержа-нием «мякоти 0%.
95 х = 10 ∙ х + 0
Слайд 12 Имеется два сплава с разным содержанием золота. В первом сплаве
Задача 10.
20 : 5 = 4 : 1
Совсем просто!!!