класс, г.Сургут
Руководитель Бадаква Людмила Абакировна
учитель математики МБОУ СОШ №7
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к проекту Комбинаторика в лоскутах
Содержание
- 1. Презентация к проекту Комбинаторика в лоскутах
- 2. Цель работы: применение комбинаторики в «Лоскутной технике».Поставлены
- 3. Гипотеза: комбинаторика имеет широкую практическую направленность в лоскутной техники
- 4. История развития комбинаторики Комбинаторика – ветвь математики,
- 5. История развития комбинаторики Первым рассматривал комбинаторику как
- 6. История развития комбинаторики Комбинаторными задачами интересовались
- 7. История развития «Лоскутной техники» «Лоскутная техника»
- 8. Методы решения комбинаторных задач Перебор возможных вариантовДерево возможных вариантовПравило умножения
- 9. Изготовление игольниц Задача: изготовить игольницы из
- 10. Первая серия игольниц: я взяла 3 лоскутка
- 11. Используя дерево возможных вариантов, получилось
- 12. Вторая серия игольниц: из 4
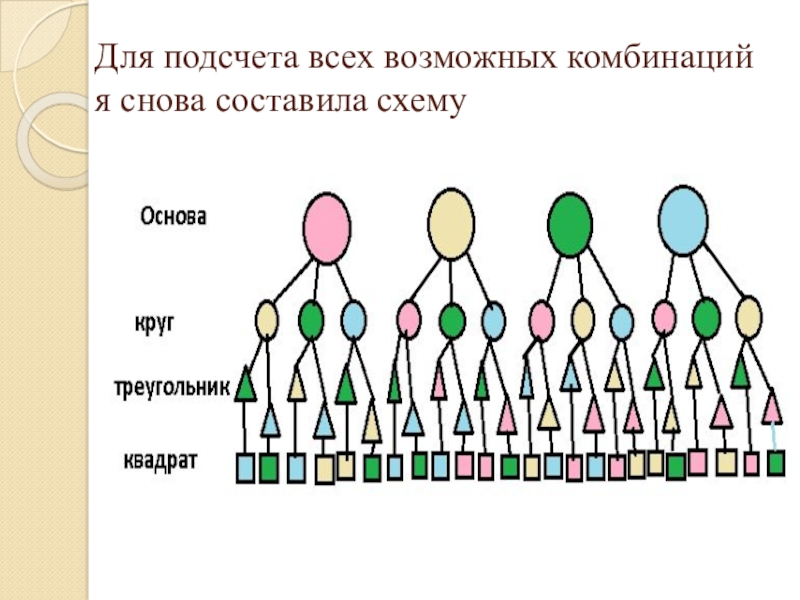
- 13. Для подсчета всех возможных комбинаций я снова составила схему
- 14. Используя дерево возможных вариантов,
- 15. Первая серия игольниц
- 16. Вторая серия игольниц
- 17. Вывод:Рассмотрев использование комбинаторики в одном из видов
- 18. Благодарю за внимание
Цель работы: применение комбинаторики в «Лоскутной технике».Поставлены задачи: подбор и изучение литературы о истории развития комбинаторики, изучение истории развития «Лоскутной техники», проведение перебора вариантов построения комбинаций геометрического рисунка при изготовлении игольниц, анализ результатов перебора и результатов
Слайд 1исследовательская работа
КОМБИНАТОРИКА В ЛОСКУТАХ
Автор: Петракова Мария Сергеевна
МБОУ СОШ №7, 5Б
Слайд 2Цель работы: применение комбинаторики в «Лоскутной технике».
Поставлены задачи: подбор и изучение
литературы о истории развития комбинаторики, изучение истории развития «Лоскутной техники», проведение перебора вариантов построения комбинаций геометрического рисунка при изготовлении игольниц, анализ результатов перебора и результатов подсчета по формулам комбинаторики.
Слайд 4История развития комбинаторики
Комбинаторика – ветвь математики, изучающая комбинации и перестановки предметов.
С
задачами, получившими название комбинаторных люди сталкивались в глубокой древности. В Древнем Китае увлеклись составлением магических квадратов. В Древней Греции подсчитывали число различных комбинаций длинных и коротких слов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата. Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д.
Слайд 5История развития комбинаторики
Первым рассматривал комбинаторику как самостоятельную ветвь науки всемирно известный
немецкий учёный Готфрид Вильгельм Лейбниц. В 1666 году Лейбниц опубликовал «Рассуждения о комбинаторном искусстве».
Слайд 6
История развития комбинаторики
Комбинаторными задачами интересовались и математики, занимавшиеся составлением и разгадыванием
шифров, изучением древних письменностей.
Теперь комбинаторика находит приложения во многих областях науки: в биологии, где она применяется для изучения состава белков и ДНК, в химии, механике сложных сооружений и т.д. Комбинаторные задачи физики, химии, биологии, экономики и других наук, которые не поддавались ранее решению из-за трудоемкости вычислений, стали успешно решаться на ЭВМ. В результате этого комбинаторные методы исследования все глубже проникают во многие разделы науки и техники.
Теперь комбинаторика находит приложения во многих областях науки: в биологии, где она применяется для изучения состава белков и ДНК, в химии, механике сложных сооружений и т.д. Комбинаторные задачи физики, химии, биологии, экономики и других наук, которые не поддавались ранее решению из-за трудоемкости вычислений, стали успешно решаться на ЭВМ. В результате этого комбинаторные методы исследования все глубже проникают во многие разделы науки и техники.
Слайд 7
История развития «Лоскутной техники»
«Лоскутная техника» - это один из видов прикладного
искусства.
Лоскутная мозаика известна очень давно. Ее применяли вместе с другими технологиями шитья, когда создавали одежду и предметы интерьера из ткани.
Музеи России собирают и изучают лоскутное шитье как вид современного искусства и постепенно растет интерес к этому виду художественного творчества.
Лоскутная мозаика известна очень давно. Ее применяли вместе с другими технологиями шитья, когда создавали одежду и предметы интерьера из ткани.
Музеи России собирают и изучают лоскутное шитье как вид современного искусства и постепенно растет интерес к этому виду художественного творчества.
Слайд 8
Методы решения комбинаторных задач
Перебор возможных вариантов
Дерево возможных вариантов
Правило умножения
Слайд 9Изготовление игольниц
Задача: изготовить игольницы из лоскутков ткани, имеющих форму
различных геометрических фигур разного размера и цвета.
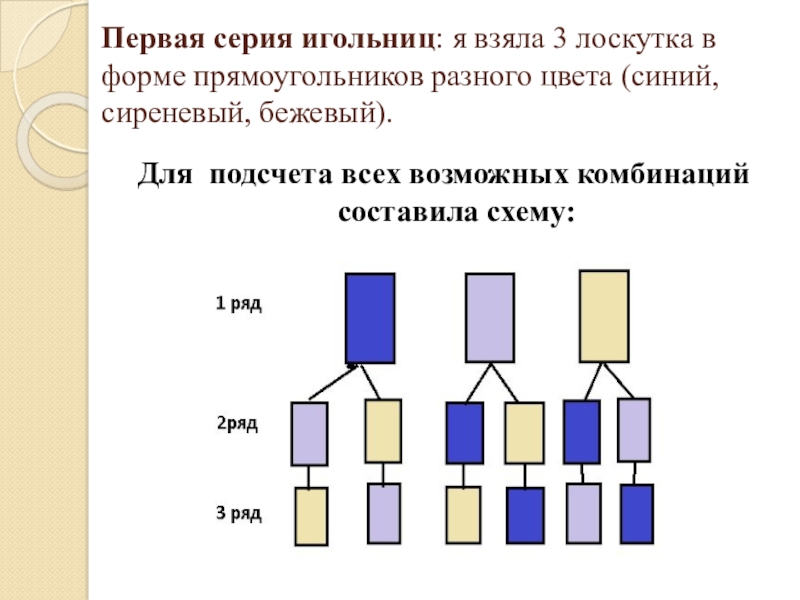
Слайд 10Первая серия игольниц: я взяла 3 лоскутка в форме прямоугольников разного
цвета (синий, сиреневый, бежевый).
Для подсчета всех возможных комбинаций составила схему:
Слайд 11 Используя дерево возможных вариантов, получилось 6 способов изготовления игольниц.
При изготовлении рисунка из трех прямоугольников разного цвета можно применить правило умножения
3*2*1 = 6 способов
Слайд 12 Вторая серия игольниц: из 4 лоскутков в форме прямоугольников
разного цвета (розовый, бежевый, зеленый, голубой). При изготовления рисунка комбинировать лоскутки по цвету и выбрать для основы игольницы один из тканей, а остальные три сформировать в аппликацию из трех геометрических фигур (квадрат, треугольник, круг).
Слайд 14 Используя дерево возможных вариантов, получилось 24 способа изготовления
игольниц.
При изготовлении рисунка из четырех лоскутов разного цвета можно применить правило умножения
4*3*2*1 = 24 способа
При изготовлении рисунка из четырех лоскутов разного цвета можно применить правило умножения
4*3*2*1 = 24 способа
Слайд 17Вывод:
Рассмотрев использование комбинаторики в одном из видов прикладного искусства – «лоскутной
технике», мы показали практическую значимость комбинаторики как области математики.
Таким образом мы подтвердили гипотезу: комбинаторика – это раздел математики, который имеет широкую практическую направленность в лоскутной технике.
Таким образом мы подтвердили гипотезу: комбинаторика – это раздел математики, который имеет широкую практическую направленность в лоскутной технике.