- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к проектной работе по математике Геометрическое решение алгебраических задач
Содержание
- 1. Презентация к проектной работе по математике Геометрическое решение алгебраических задач
- 2. Цель работы:Рассмотреть различные геометрические методы в решении
- 3. Слайд 3
- 4. Решение алгебраических задач с помощью теоремы Пифагора.Решите
- 5. Решите систему уравнений при условии, что x,
- 6. Применение в решении задач теоремы, обратной теореме
- 7. Решение текстовых задачНа двух типографских станках, работающих
- 8. Расстояние между двумя городами равно 450 км.
- 9. Задачи с практическим применениемЗадача «О судне». Парусное
- 10. Решение квадратного уравнения с помощью циркуля и
- 11. Решить квадратное уравнение 7х2-6х-1=0.Решение:1) Построим точки S (-b/2a;
- 12. Графический способ решения алгебраических систем уравнений и
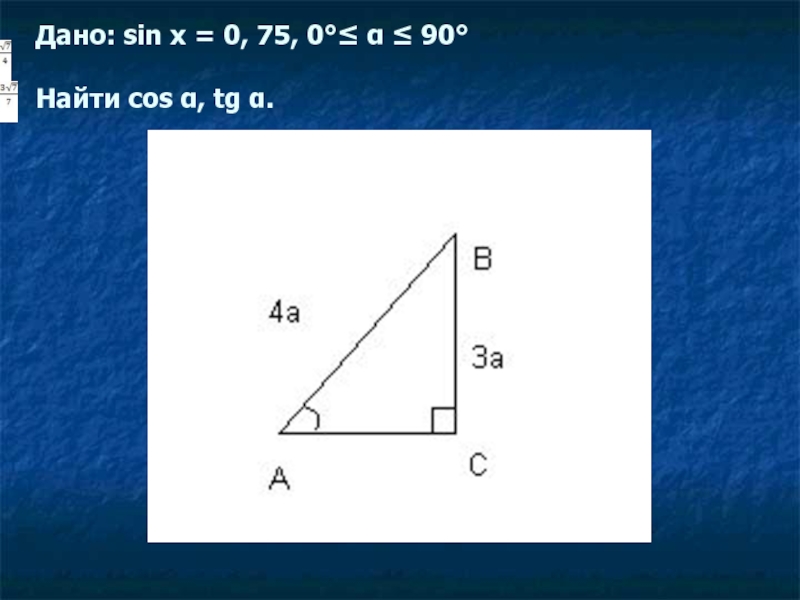
- 13. Дано: sin x = 0, 75, 0°≤
- 14. Геометрическое решение некоторых нестандартных задачПри каком а
- 15. ЗаключениеГеометрия придает алгебре необыкновенную красоту и изящность.
Слайд 1
Геометрические решения алгебраических задач
Выполнили: Мануйлова Валентина и Овчарова Наталья
ученицы
Руководитель: учитель математики ВКК Кобелева Татьяна Васильевна.
2014
Слайд 2
Цель работы:
Рассмотреть различные геометрические методы в решении алгебраических задач.
Задачи работы:
1) показать, что преимущество геометрического решения алгебраических задач в его наглядности, так как геометрический подход допускает изящные решения;
2) рассмотреть применение теоремы Пифагора и обратной ей теоремы для решения алгебраических задач;
3) рассмотреть применение метода линейных и двумерных диаграмм для решения алгебраических задач;
4) продемонстрировать применение геометрического метода для решения текстовых задач.
Слайд 3
Решение: Пусть х-расстояние от
лестницы до стены (рис. 2)
По теореме Пифагора:
1172+ х2=1252
х2=1936; х=44 , так как х>0
Ответ: 44 стопы.
Задача из «Арифметики» Магницкого
Слайд 4Решение алгебраических задач с помощью теоремы Пифагора.
Решите уравнение :
«Найдите катет х
В результате получаем |х|=5, а значит, х=±5.
Ответ: х=±5.
Слайд 5Решите систему уравнений при условии, что x, y, z и t
Решение:
Треугольник AВС с прямым углом С (рис. 4b), у которого катет АС = 8, поскольку сумма длин соответствующих катетов равна 8. Катет ВС = 6,
так как x + у + z + t = 6. тогда гипотенуза
АВ = =10. Отсюда следует, что
гипотенузы рассматриваемых
треугольников лежат на одной прямой,
потому что в противном случае длина
ломаной AFEDB была бы строго больше
10.Точки F, E и D делят гипотенузу
АВ на части, которые относятся
BD:DE:EF:FA = 1:2:3:4. Проведем
через эти точки прямые,
параллельные катету АС. По теореме
о пропорциональных отрезках катет
ВС разделился в том же отношении,
т.е. x:y:z:t = 1:2:3:4.
Ответ: x = 0,6, y = 1,2, z = 1,8, t = 2,4.
Слайд 6Применение в решении задач теоремы, обратной теореме Пифагора.
. Из условий х2+у2=9,
Решение:
По теореме, обратной теореме Пифагора , числах, у и 3 являются соответственно длинами катетов и гипотенузы треугольника АВD с прямым углом D. Из 2-го уравнения у, z и 4 так же есть
соответственно длины катетов и гипотенузы
треугольника ВСD с прямым углом D.
Третье уравнение системы разрешает
утверждать, что число у есть среднее
пропорциональное чисел х и z,
и по теореме, обратной теореме о
пропорциональных отрезках в
прямоугольном треугольнике,
угол АВС – прямой (рис).
Теперь рассмотрим выражение
ху+уz. ху+уz=(х+z)у= 2SAВС=3•4=12.
Ответ: ху+уz=12
Слайд 7Решение текстовых задач
На двух типографских станках, работающих одновременно, можно сделать копию
Решение:
На оси абсцисс откладываем время работы станков в минутах. Оба станка сделают работу вместе за 10 минут. ОМ=10. Тогда одной первой понадобится t минут. А второй (t+15) минут.V - объем работ, который нужно выполнить. ОВ - график работы первого станка, ОС - второго, ОА – вместе (рис. 9). ΔОVB≅ΔNAB и ΔOPС≅ΔOMK, откуда
VO/AN=VB/AB и СP/KM=OP/OM; покажем, что
AN=KM. Так как за 10 минут первый станок
выполнит часть работы, соответствующий отрезку
NM (AN - отрезок работы который выполнит второй станок).
Но за 10 минут второй станок выполнит часть работы,
соответствующую МК. Поэтому АN=КМ.
Учитывая это равенство и то, что СР=VO, получаем,
VO/AN=CP/KM. Так как VO/AN=VB/AB и
СP/KM=OP/OM, то получаем соотношение: VB/AB=OP/OM, значит t/(t-10)=(t+15)/10; t2-5t-150=0; t=15 Таким образом, I станок выполнит работу за 15 минут, а II за 30 минут.
Ответ: 15 минут, 30 минут.
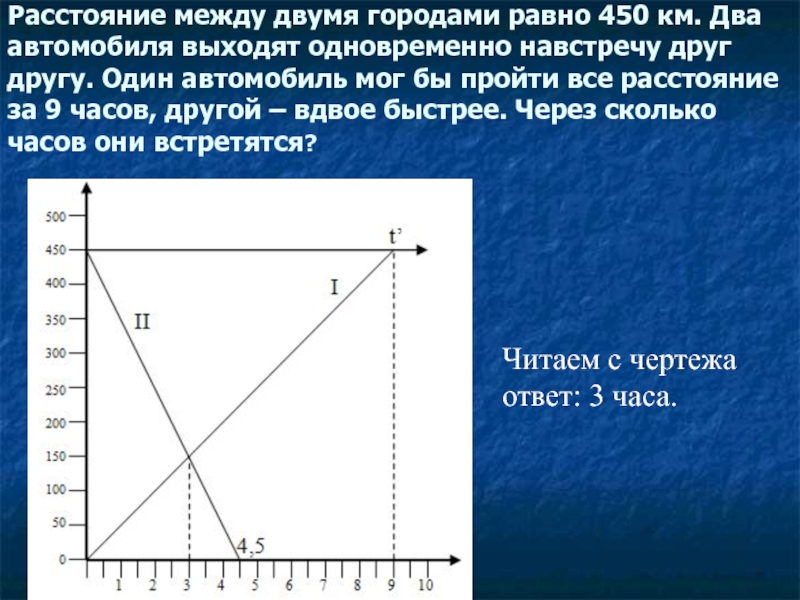
Слайд 8Расстояние между двумя городами равно 450 км. Два автомобиля выходят одновременно
Читаем с чертежа ответ: 3 часа.
Слайд 9Задачи с практическим применением
Задача «О судне».
Парусное судно стояло на
Решение:
По теореме Пифагора 122+52=144+25=169; 13•4=52 (м)
Ответ: троса не хватило
Слайд 10Решение квадратного уравнения с помощью циркуля и линейки
Найдите корни квадратного уравнения
Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1;0) и С(х2;0) где х1 и х2 –корни квадратного уравнения ax2+bx+c=0, и проходит через точку А(0;1) (рис). Тогда по теореме о секущих имеем OС×OВ=OЕ×OА, откуда OЕ= =(OB×OС)/OA=(x1×x2)/1=c/a.
Центр окружности -точка пересечения
перпендикуляров SF и SK, восстановленных в
серединах хорд АЕ и BС , поэтому
ОК=(x1+x2)/2=-b/2a,ОF=(1+c/a)/2=(a+c)/2a.
Способ нахождения
корней квадратного уравнения ax2+bx+c=0
с помощью циркуля и линейки:
построим точки S (-b/2a; (a+c)/2a) – центр
окружности и А(0;1);
2) проведем окружность радиуса SA;
3) абсциссы точек пересечения этой
окружности с осью Оx являются корнями исходного
квадратного уравнения (рис).
Слайд 11Решить квадратное уравнение 7х2-6х-1=0.
Решение:
1) Построим точки S (-b/2a; (a+c)/2a) =S(3/7; 3/7) -
2) Проведем окружность радиуса SA (рис. 4);
3) Окружность пересекает
ось абсцисс в точках (-1/7;0)
и (1;0)
4) Проверкой убеждаемся,
что х1=−1/7; х2=1 –
корни данного уравнения.
Ответ: х1=−1/7; х2=1
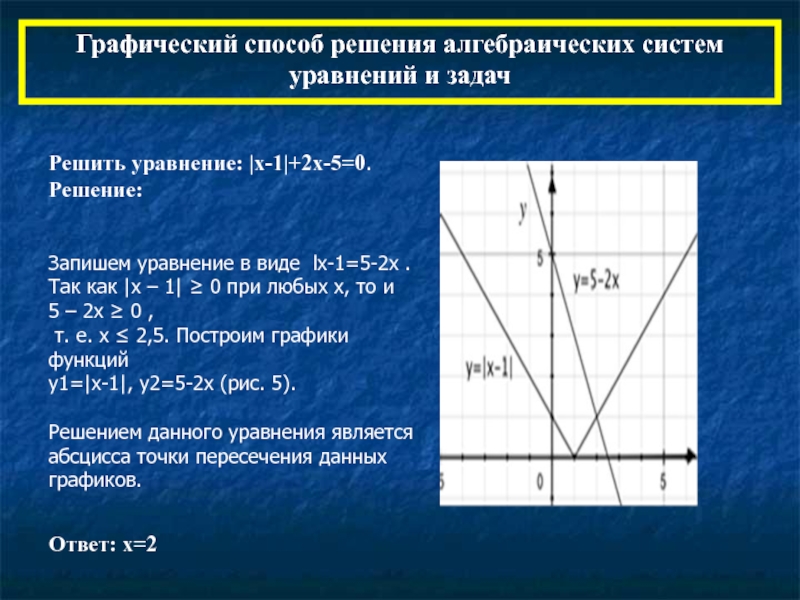
Слайд 12Графический способ решения алгебраических систем уравнений и задач
Решить уравнение: |x-1|+2x-5=0.
Решение:
Запишем уравнение в виде lx-1=5-2х .
Так как |x – 1| ≥ 0 при любых х, то и
5 – 2x ≥ 0 ,
т. е. x ≤ 2,5. Построим графики
функций
у1=|x-1|, y2=5-2x (рис. 5).
Решением данного уравнения является
абсцисса точки пересечения данных
графиков.
Ответ: х=2
Слайд 14Геометрическое решение некоторых нестандартных задач
При каком а система уравнений имеет ровно
Решение:
Построим линии, определяемые
уравнениями системы (рис. 9).
Четыре решения могут быть
только в двух случаях,
когда. a = R2 =1 или a = r2 =1/2
Ответ:1; 1/2
Слайд 15Заключение
Геометрия придает алгебре необыкновенную красоту и изящность. А вместе алгебра и
геометрические подходы часто
упрощают решение задач.
Геометрия-