- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад исследовательской работы Зурхайн самбар (счетная доска монгольских народов)
Содержание
- 1. Презентация исследовательской работы Зурхайн самбар (счетная доска монгольских народов)
- 2. Слайд 2
- 3. История возникновенияИстоки происхождения счетной доски историки математики
- 4. С ХVI в. при решениях задач "зурхайши"
- 5. Доска имела
- 6. Термин “зурхай” буквально означает “черта, линия” и
- 7. Монгольский зурхай означал своеобразный алгоритм математического вычисления,
- 8. Единственная копия "зурхайн самбар" сохранилась до наших
- 9. Примеры вычислений:
- 10. ПРИМЕР 512-89=423 Уменьшаемое 512 112 2
- 11. Умножение. Деление. Особое внимание уделяется на размещение
- 12. Исчисление на счетной доске имело особенность: из-за
- 13. Счастлив как
- 14. Слайд 14
- 15. Литература:Б. Батжаргал. Эртний монголын математик (Ранняя математика
Слайд 1
«Зурхайн самбар»
Счетная доска монгольских народов
Номинация «Старинные задачи»
Гусейнов Элвин, Дмитриева Дарья
Ученики 8
Руководитель: Барташкина Ольга Вячеславовна, учитель математики
Слайд 2
использовали самобытный счетный прибор "зурхайн самбар" для математических и астрономических вычислений, имели интересные культурные традиции, связанные с ними. Математика средневековой Монголии уже с ХIII в. развивалась как совокупность алгоритмов для решения математических, астрономических, астрологических задач – зурхай.
Слайд 3История возникновения
Истоки происхождения счетной доски историки математики относят к Индии, где
Слайд 4
С ХVI в. при решениях задач "зурхайши" – монгольские специалисты производили
Слайд 5
Доска имела очертания панциря черепахи, на
Слайд 6
Термин “зурхай” буквально означает “черта, линия” и происходит, вероятно, от слова
Слайд 7
Монгольский зурхай означал своеобразный алгоритм математического вычисления, основанный на закономерной повторяемости
В зурхае применялось десять цифр. Все математические вычисления по зурхаю производились на специальной доске (так называемая зурхайн самбар).
Слайд 8
Единственная копия "зурхайн самбар" сохранилась до наших дней в архиве монастыря
Слайд 9Примеры вычислений:
При сложении и
Действия производятся, начиная со старших, а не с младших разрядов,
2. Знаки действия не ставятся,
3. Ответы формируются в ходе вычислений в верхней строчке, при этом особое внимание обращается на переход через десяток
4. Промежуточные результаты стираются в процессе счёта, так что непосредственную проверку выполнить невозможно.
Слайд 10
ПРИМЕР 512-89=423
Уменьшаемое 512 112 2 12
Вычитаемое 89 89
Разность 4 43 42 423
ПРИМЕР 645+87=732
Слагаемое 645 45 1 5 5 1
слагаемое 87 87 7 7 2 3 4 5 6 1 2 3 4 5 1
Сумма 6 62 72 722 732
.
Слайд 11
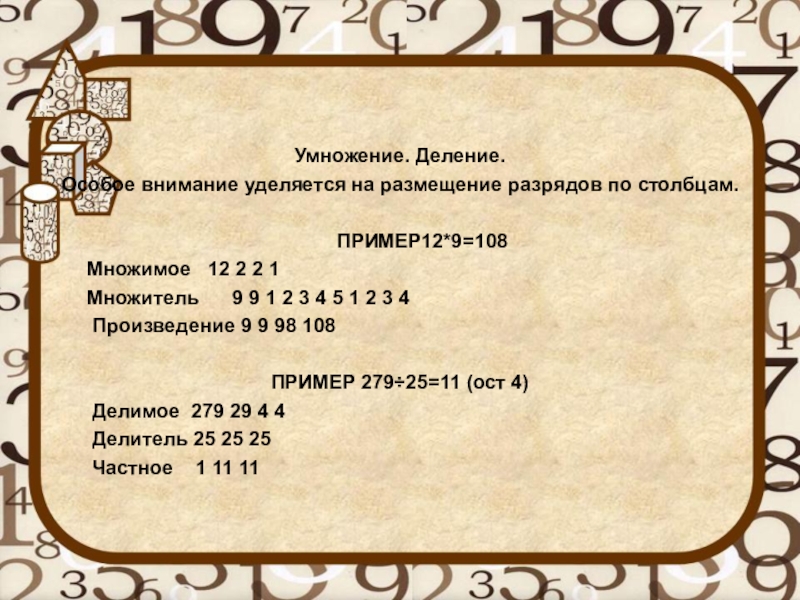
Умножение. Деление.
Особое внимание уделяется на размещение разрядов по столбцам.
Множимое 12 2 2 1
Множитель 9 9 1 2 3 4 5 1 2 3 4
Произведение 9 9 98 108
ПРИМЕР 279÷25=11 (ост 4)
Делимое 279 29 4 4
Делитель 25 25 25
Частное 1 11 11
Слайд 12
Исчисление на счетной доске имело особенность: из-за небольшого размера промежуточные вычисления
Слайд 13 Счастлив как Чингисхан. Часть 3. Есугей
Много времени проводит Бартан, склонившись над зурхайской доской. Она напоминает панцирь черепахи с двенадцатью крупными чешуями. На каждой – одно из животных зодиакального временного цикла. Десять цифр позволяют складывать и вычитать, делить и умножать, производить алгебраические, геометрические и тригонометрические действия, связанные с астрономией. Особая, зурхайская таблица умножения позволяет Бартану проверять правильностьрешения задач, требующих гибкости ума и сообразительности. Бартан вычисляет по своим календарям положение и движение семи планет и 28 звезд относительно двенадцатиханной юрты, даты опасных для скотоводов природных явлений и солнечных затмений, начало и конец девяти девяток - холодного сезона года, особенно средней, самой суровой девятки.
Слайд 15Литература:
Б. Батжаргал. Эртний монголын математик (Ранняя математика монголов). Улан-Батор, 1976. Н.
http://forum.http://forum.mongoliayhttp://forum.mongoliay.ru/topic/7241
http://polusharie.com