- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад интегрированного урока геометрии и МХК
Содержание
- 1. Презентация интегрированного урока геометрии и МХК
- 2. Цели и задачи урока:Вспомнить материал из планиметрии
- 3. Определение:
- 4. Иллюстрация для случая скрещивающихся прямых (красная и
- 5. Ротонда московской усадьбы «Дурасово»Вопрос №2: Сколько прямых
- 6. Теперь напомним очень важную теорему о параллельных
- 7. А ВЕще
- 8. Вопрос №3: Желтые прямые на ступеньках дворца
- 9. Теперь нам предстоит познакомиться с очень важным
- 10. Часто решение геометрических задач
- 11. Дано: М – середина BD ABDCNMРQN –
- 12. ABDCNMРQ РЕШЕНИЕ:PQ- средняя линия треугольника АВС, тогда
- 13. Параллельные прямыеВопрос №8: Могут ли три параллельныхпрямых не лежать в одной плоскости?Параллельные прямые в интерьере дворца
- 14. КРАТКИЕ ИТОГИ УРОКА: На уроке мы
- 15. ДОМАШНЕЕ ЗАДАНИЕ: повторить свойства средней линии трапеции;
Слайд 1
Параллельные
прямые в
архитектуре
московской
усадьбы
«Дурасово»
Г.Г.Воронцов
учитель
ГОУ СОШ № 1148
им. Ф.М.Достоевского
Слайд 2Цели и задачи урока:
Вспомнить материал из планиметрии о параллельности прямых на
2) Рассмотреть взаимное расположение двух прямых в пространстве.
Ввести понятие параллельных и скрещивающихся прямых;
Вспомнить свойства параллельных прямых на плоскости и познакомиться
со свойствами параллельных прямых в пространстве;
закрепить понимание этих свойств на архитектурных элементах зданий
и интерьеров
московской усадьбы .
5) Научится применять свойства параллельных прямых к решению задач.
Слайд 3 Определение: Параллельными прямыми в пространстве называются прямые, 1)лежащие в одной плоскости и
Взаимное расположение прямых в пространстве:
две различные прямые в пространстве
либо пересекаются в одной точке,
либо не пересекаются (не имеют общих точек).
Второй случай допускает две возможности:
прямые могут лежать в одной плоскости (параллельны) или
не лежать в одной плоскости (скрещивающиеся прямые).
Слайд 4
Иллюстрация для случая скрещивающихся прямых
(красная и зеленая прямые лежат в
и не пересекаются)
Вопрос №1: Пересекаются ли в действительности
зеленая и красная прямые линии в пространстве (красная линия
проведена по колонне, а зеленая линия проведена по карнизу?
Слайд 5Ротонда московской усадьбы «Дурасово»
Вопрос №2: Сколько прямых переплета внешней рамы
Слайд 6Теперь напомним
очень важную теорему
о параллельных прямых
в пространстве:
«Через точку,
на прямой можно провести
параллельную прямую
и при том только одну».
α
A m
n
Барельеф большого
торцевого окна дворца
Слайд 7
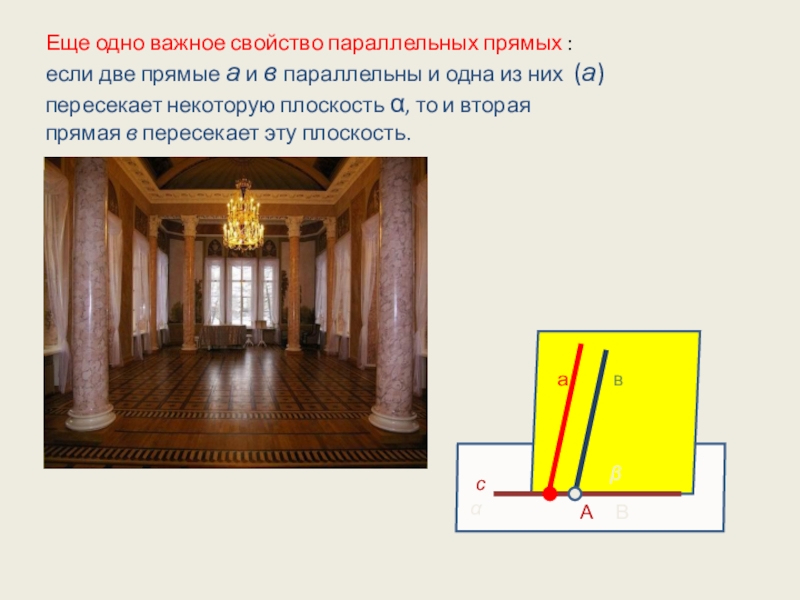
А В
Еще одно важное свойство параллельных
если две прямые а и в параллельны и одна из них (а) пересекает некоторую плоскость α, то и вторая прямая в пересекает эту плоскость.
β
с
α
а в
Слайд 8
Вопрос №3:
Желтые прямые на ступеньках
дворца параллельны?
Вопрос №4:
Если
параллельны, то пересекают ли они
плоскость в которой лежат
желтые линии?
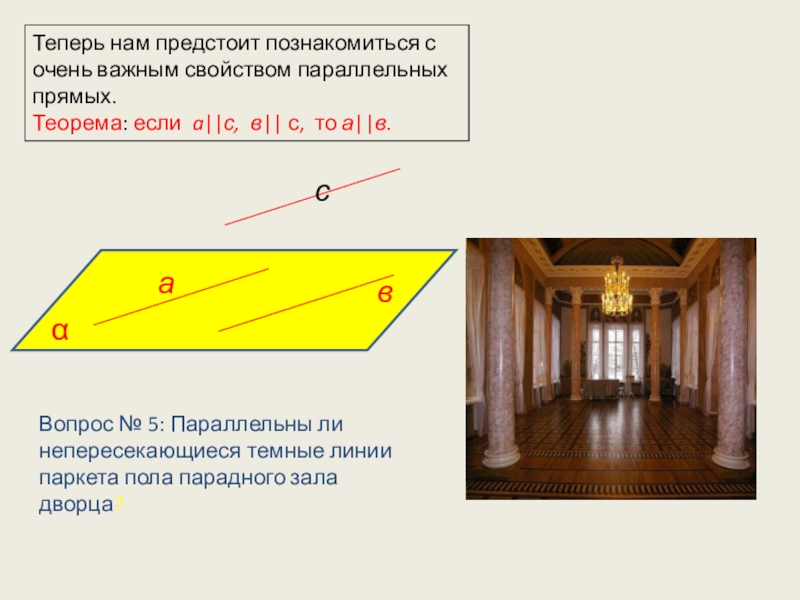
Слайд 9Теперь нам предстоит познакомиться с очень важным свойством параллельных
прямых.
Теорема: если a||с,
α
а
в
с
Вопрос № 5: Параллельны ли непересекающиеся темные линии паркета пола парадного зала дворца?
Слайд 10 Часто решение геометрических задач в пространстве
сводится к
применению свойств плоских фигур.
Для решения задачи на нашем уроке необходимо вспомнить о средней линии треугольника и ее свойствах:
средней линией треугольника называется линия,
соединяющая середины двух сторон треугольника;
2) средняя линия треугольника, проведенная через две стороны, параллельна третьей стороне треугольника и равна ее половине.
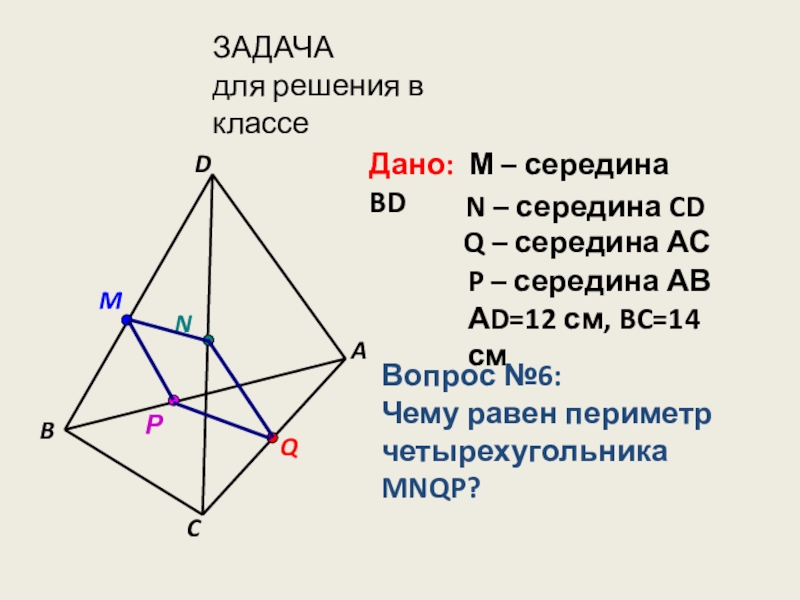
Слайд 11Дано: М – середина BD
A
B
D
C
N
M
Р
Q
N – середина CD
Q – середина
P – середина АВ
АD=12 см, BC=14 см
Вопрос №6:
Чему равен периметр
четырехугольника MNQP?
ЗАДАЧА
для решения в классе
Слайд 12
A
B
D
C
N
M
Р
Q
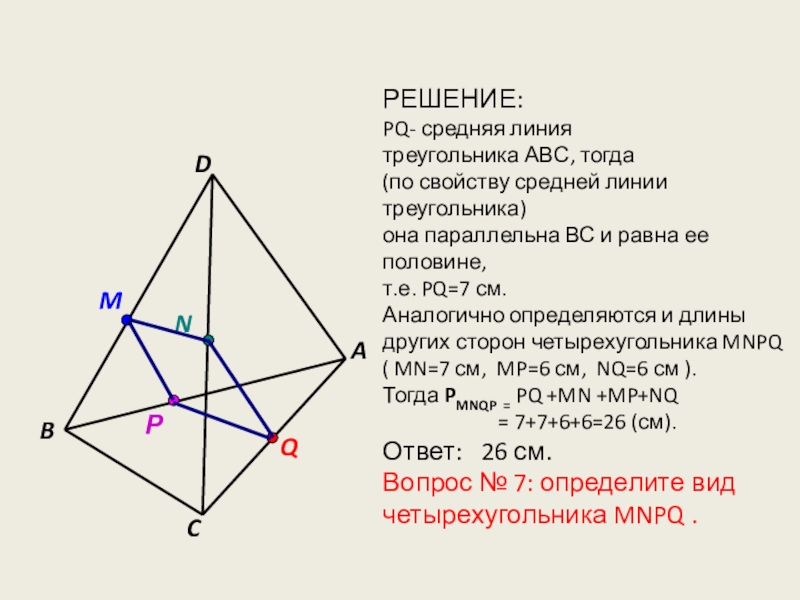
РЕШЕНИЕ:
PQ- средняя линия
треугольника АВС, тогда
(по свойству средней линии
она параллельна ВС и равна ее половине,
т.е. PQ=7 см.
Аналогично определяются и длины
других сторон четырехугольника MNPQ
( MN=7 см, MP=6 см, NQ=6 см ).
Тогда PMNQP = PQ +MN +MP+NQ
= 7+7+6+6=26 (см).
Ответ: 26 см.
Вопрос № 7: определите вид
четырехугольника MNPQ .
Слайд 13
Параллельные прямые
Вопрос №8:
Могут ли три параллельных
прямых не лежать
в одной
Параллельные
прямые
в интерьере дворца
Слайд 14КРАТКИЕ ИТОГИ УРОКА:
На уроке мы узнали:
какие прямые называются
в пространстве;
рассмотрели возможные случаи взаимного
расположения прямых в пространстве
(пересекающиеся, параллельные и
скрещивающиеся);
- вспомнили о свойствах параллельных прямых в
пространстве;
познакомились с теоремой: если a||с, в|| с, то а||в;
решили задачу.
Слайд 15ДОМАШНЕЕ ЗАДАНИЕ:
повторить свойства средней линии трапеции;
выучить определения и свойства
сегодняшнего урока;
3) решить задачу №16.