- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Графы вокруг нас
Содержание
- 1. Презентация Графы вокруг нас
- 2. С дворянским титулом «граф» тему моей работы
- 3. Цель:Изучение основных понятий теории графов, сферы деятельности
- 4. История возникновения графовТермин «граф» впервые появился в
- 5. Леонард Эйлер (1707-1783)Леонард Эйлер (1707-1783)-швейцарец по происхождению. Приехал в
- 6. В России изучением теории графов занимались ученые:Лев
- 7. Основные положения теории графовГрафом называется конечное множество
- 8. Количество рёбер, выходящих из вершины графа, называется
- 9. Благодаря Леонарду Эйлеру существует общий прием решения
- 10. Задача о Кенигсбергских мостах
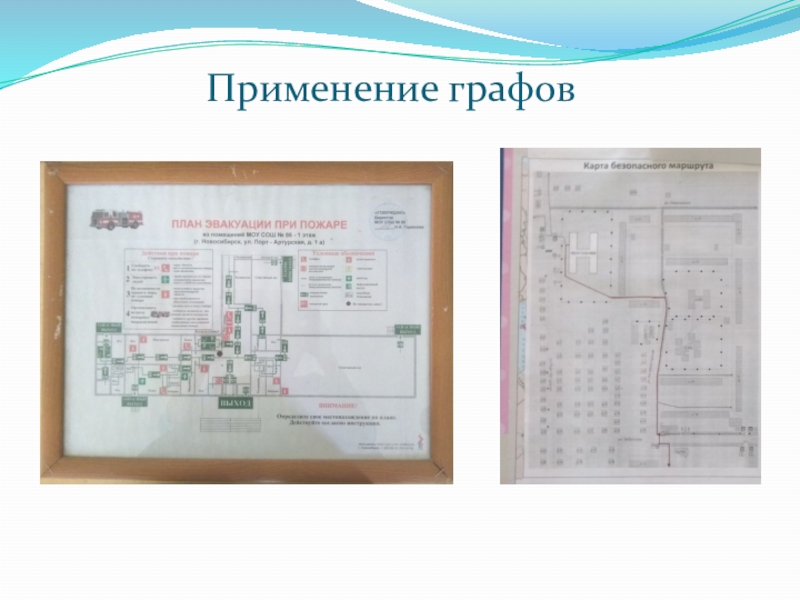
- 11. Применение графов
- 12. Применение графов
- 13. Применение графов Менеджер по логистике занимается
- 14. система улиц города;схема железных и шоссейных дорог; план выставки УчСиб – 2018. Применение графов. Графом является:
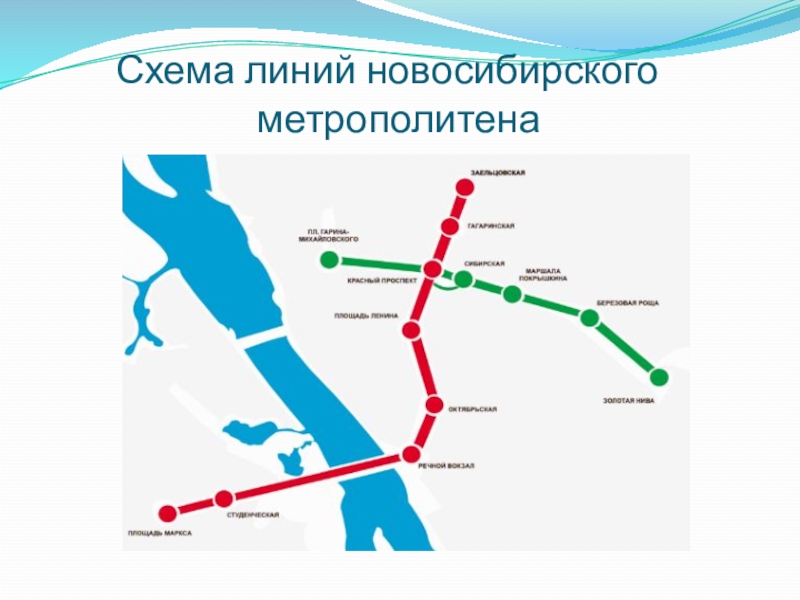
- 15. Схема линий новосибирского метрополитена
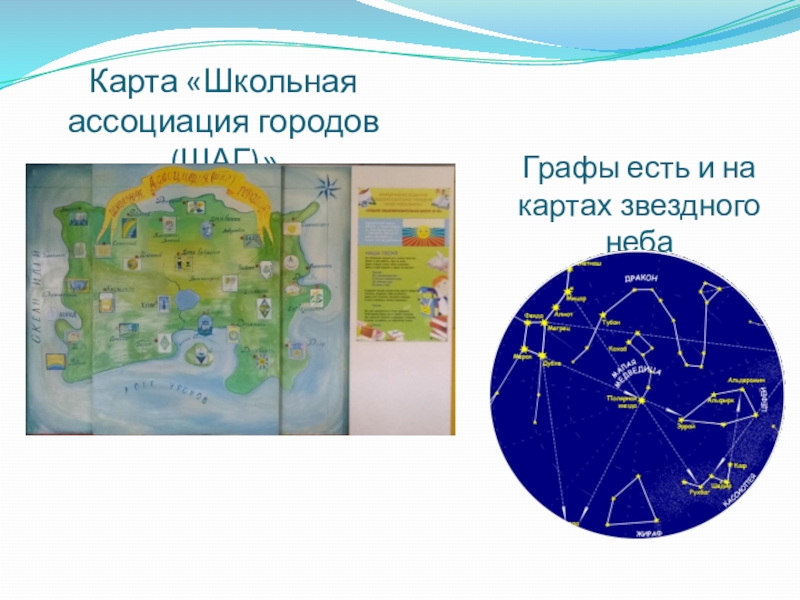
- 16. Графы есть и на картах звездного небаКарта «Школьная ассоциация городов (ШАГ)»
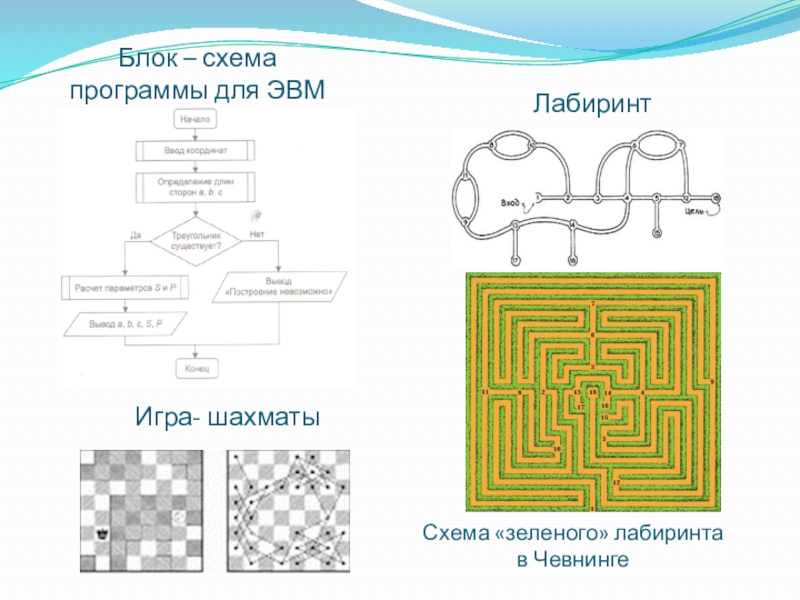
- 17. Блок – схема программы для ЭВМ
- 18. Самым впечатляющим примером графа в современном мире
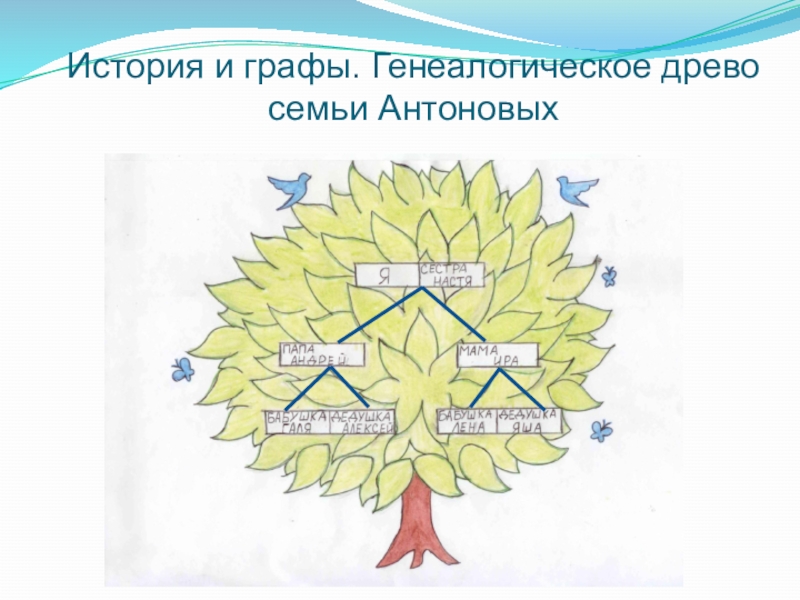
- 19. История и графы. Генеалогическое древо семьи Антоновых
- 20. АнкетированиеГрафы помогают при решении задач? (Да -
- 21. Внеклассное мероприятие «Графы вокруг нас»
Слайд 1Графы вокруг нас
Автор: Антонова Александра Андреевна
МБОУ СОШ № 86, 5 «Г»
Ленинский район г. Новосибирска
Руководитель проекта: Спиридонова
Светлана Николаевна
Слайд 2С дворянским титулом «граф» тему моей работы связывает общее происхождение от
Теория графов зародилась в ходе решения головоломок почти 300 лет назад.
Гипотеза:
Граф помогает в решении задач, имеет практическое применение в жизни.
Слайд 3
Цель:
Изучение основных понятий теории графов, сферы деятельности человека на предмет применения
Задачи:
проанализировать литературу, изучить основные теоретические понятия;
узнать о применении графов в разных предметных областях и в различных сферах деятельности.
изучить методы решения задач с помощью графов;
проанализировать основные типы задач, решаемых с помощью графов;
составить сборник материалов на применение графов в разных предметных областях, изготовить лэпбук;
апробировать задачи на уроках и внеклассных мероприятий;
провести анкетирование, оформить проект, подготовить презентацию.
Слайд 4История возникновения графов
Термин «граф» впервые появился в книге «Теория конечных и
Слайд 5Леонард Эйлер (1707-1783)
Леонард Эйлер (1707-1783)-швейцарец по происхождению. Приехал в Санкт-Петербург в 1727 году.
Слайд 6В России изучением теории графов занимались ученые:
Лев Семёнович Понтрягин (1908 -1988);
Александр
Слайд 7Основные положения теории графов
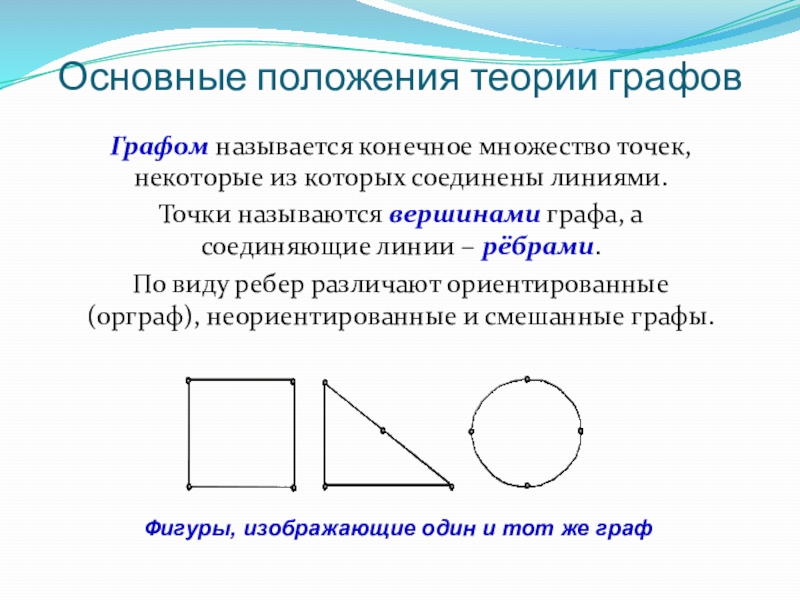
Графом называется конечное множество точек, некоторые из которых
Точки называются вершинами графа, а соединяющие линии – рёбрами.
По виду ребер различают ориентированные (орграф), неориентированные и смешанные графы.
Фигуры, изображающие один и тот же граф
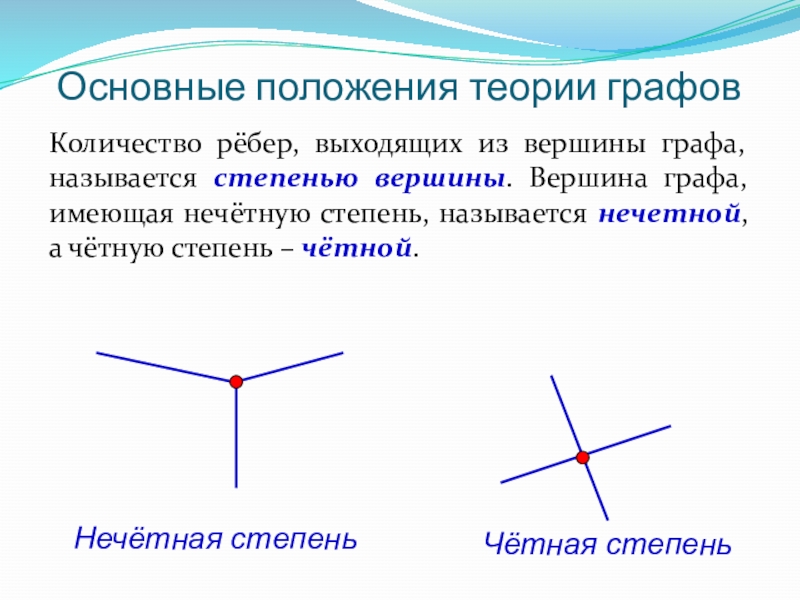
Слайд 8Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа,
Нечётная степень
Чётная степень
Основные положения теории графов
Слайд 9Благодаря Леонарду Эйлеру существует общий прием решения подобных задач:
преобразовать рисунок в
определить степень каждой вершины;
посчитать количество нечётных вершин;
сделать выводы:
а) заданный обход возможен, если:
Все вершины чётные. Обход можно начать с любой вершины.
Две вершины нечётные. Обход нужно начать с одной из нечётных вершин.
б) заданный обход невозможен, если нечётных вершин больше двух;
указать начало и конец пути.
Одним росчерком
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым.
Слайд 13Применение графов
Менеджер по логистике занимается доставкой товаров, грузов,
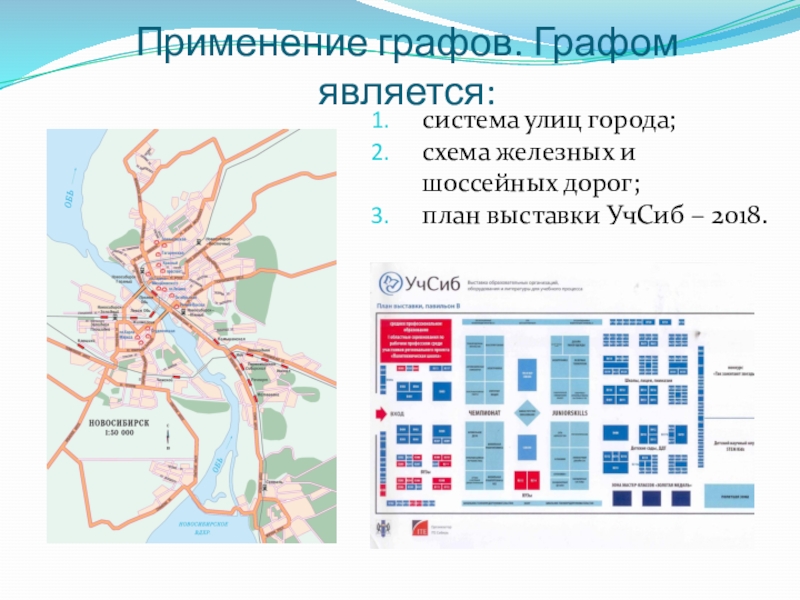
Слайд 14система улиц города;
схема железных и шоссейных дорог;
план выставки УчСиб –
Применение графов. Графом является:
Слайд 18Самым впечатляющим примером графа в современном мире выступает Интернет. Его узлы
Другая сложная система, появившаяся гораздо раньше Интернета - глобальная общемировая телефонная сеть - также является графом.
Интернет- это граф
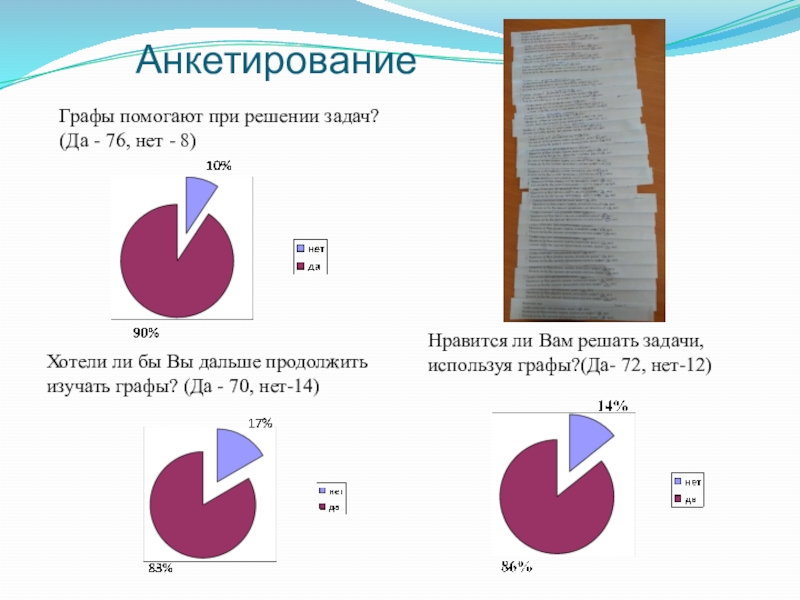
Слайд 20Анкетирование
Графы помогают при решении задач? (Да - 76, нет - 8)
Нравится
Хотели ли бы Вы дальше продолжить изучать графы? (Да - 70, нет-14)