- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад деловой игры по математике
Содержание
- 1. Презентация деловой игры по математике
- 2. Игра «Биржа знаний» проводится в течении 5
- 3. Перед учащимися встаёт вопрос
- 4. Основная цель участника - в
- 5. В рамках игры проводятся: открытие биржи (вторник);лотерея
- 6. ЛотереяДля игры заготовлены лотерейные билеты. Каждый билет
- 7. Спринт-олимпиада.Ученики, желающие принять участие в спринте,
- 8. Вопросы для спринт – олимпиады.1. На
- 9. 4.В полдень из Москвы отправляется поезд
- 10. 7. Три курицы за три дня
- 11. 10.«ПРИЗОВОЙ»Два человека одновременно вышли из А
- 12. 13. Груша тяжелее яблока, а яблоко
- 13. 16. В четырёхэтажном доме Ваня живёт
- 14. 19.Из трёх одинаковых по виду колец
- 15. 21.Сколькими способами можно представить число 50
- 16. 24.В шахматном турнире 3-мя участниками всего
- 17. 28.Выписаны все числа подряд от 1
- 18. 31.Напишите наименьшее десятизначное число, у которого
- 19. 36. Найдите значение выражения 13а +
- 20. Ипподром.Это оригинальная игра состоит
- 21. Первый заезд : «Скачки с препятствиями».Участникам
- 22. Второй заезд: «Математический алфавит».Выбирается одна из
- 23. Участникам заезда раздаются двухцветные сигнальные карточки.
- 24. Четвёртый заезд: «Составь слово».Участникам этого заезда
- 25. Ведущий или ассистент записывает на бумаге трёхзначное
- 26. Как и на любом аукционе, вход
- 27. Назовите пословицы и поговорки, в которых используются
- 28. Закрытие биржиВ этот день учитель подводит итоги игры, награждает победителей призами.
- 29. Альхова З.Н., Макеева А.В. «Внеклассная работа по
Слайд 2Игра «Биржа знаний» проводится в течении 5 дней среди учащихся шестых
На период игры учреждается Коммерческий атематический банк (КМБ).
Банк выпускает в обращение 2 вида ассигнаций «таланты» и «гении».
Перед началом игры КМБ выдаёт всем ученикам по 10 «талантов».
«Биржа знаний»
Коммерческий математический банк
Курс валют
1 гений = 7 талантам
Слайд 3 Перед учащимися встаёт вопрос -
«Биржа знаний»
Слайд 4
Основная цель участника - в ходе игры обменять указанную
Плата за участие в мероприятиях принимается в «талантах».
При удачном выступлении банк расплачивается «гениями».
«Гений» являлся свободно конвертируемой валютой;
во время игры он обменивался на «таланты», а по окончании - на оценки по математике.
Курс обмена ежедневно объявляется банком.
Слайд 5В рамках игры проводятся:
открытие биржи (вторник);
лотерея (в течение всей недели);
спринт-олимпиада
игра « Ипподром « (среда);
аукцион (четверг);
закрытие биржи (пятница).
Слайд 6
Лотерея
Для игры заготовлены лотерейные билеты. Каждый билет имеет номер и содержит
Цена билета 1 «талант».
Если участник справился с заданием билета, то он зарабатывает 1 «гений».
Если участник дал неправильный ответ, то лотерейный билет у него изымается.
Его можно вновь выкупить, заплатив ещё 1 «талант», и попытаться снова выполнить задание билета.
Слайд 7
Спринт-олимпиада.
Ученики, желающие принять участие в спринте, приобретают у ассистентов
Ведущий задаёт вопросы, интересные по форме и содержанию, а участник, желающий дать ответ, поднимает игровой номер.
Если ответ правильный, то ассистент вносит в соответствующую игровому номеру строку таблицы «+», если неправильный «-».
Дав неправильный ответ, игрок может попытаться повторно ответить на этот вопрос, но лишь после того, как заплатит 1 «талант».
Каждый пятый вопрос спринта - призовой, сложность его выше; за ответ на него участник получает не один, а три плюса.
После того, как вопросы исчерпаны, подводятся итоги.
Плюс и минус гасят друг друга; оставшиеся после погашения плюсы - это чистый выигрыш участника в «гениях».
Кроме того, пять лучших участников спринт - олимпиады получают право участвовать в первом заезде ипподрома бесплатно.
Слайд 8
Вопросы для спринт – олимпиады.
1. На руках 10 пальцев.
Ответ: 50 пальцев.
2. Двое играли в шашки 4 часа. Сколько часов играл каждый из них?
Ответ: 4 часа.
3. Экипаж, запряжённый тройкой лошадей, проехал за один час 15 км.
С какой скоростью бежала каждая лошадь?
Ответ: 15 км/ч.
Слайд 9
4.В полдень из Москвы отправляется поезд в Санкт-Петербург со скоростью
Ответ: На одинаковом расстоянии.
5.«ПРИЗОВОЙ»
Два пакета молока и пачка творога стоят 94 рубля. А две пачки творога и пакет молока стоят 80 рублей. Что дороже - пачка творога или пакет молока и на сколько?
Ответ: Пакет молока дороже пачки творога на 14 рублей.
6.У родителей пять сыновей. Каждый имеет одну сестру. Сколько всего детей в семье?
Ответ: 6 детей.
Слайд 10
7. Три курицы за три дня дают три яйца. Сколько
Ответ: 48 яиц.
8.Имеется 60 трёхметровых брёвен, которые надо распилить на полуметровые части. Сколько распилов придётся сделать?
Ответ: 300 распилов.
9.Во сколько раз лестница на 6-й этаж дома длиннее лестницы на 2-й этаж этого же дома?
Ответ: В 5 раз.
Слайд 11
10.«ПРИЗОВОЙ»
Два человека одновременно вышли из А в В. Первый половину
Ответ: Первый пришёл в В раньше.
11.Книга стоит 1 рубль и ещё половину стоимости книги. Сколько стоит книга?
Ответ: 2 рубля.
12. Может ли быть в одном месяце пять воскресений?
Ответ: Да, например - 1, 8, 15, 22, 29-е.
Слайд 12
13. Груша тяжелее яблока, а яблоко тяжелее персика. Что тяжелее
Ответ: Груша.
14. Ручка дороже тетради, а карандаш дешевле ручки. Что дороже – карандаш или тетрадь ?
Ответ: Нельзя ответить на этот вопрос.
15.«ПРИЗОВОЙ»
Сколько половин в числе 11,5?
Ответ: 23 половины.
Слайд 13
16. В четырёхэтажном доме Ваня живёт выше Пети, но ниже
Ответ: Вася на 1-ом, Петя на 2-ом, Ваня на 3-ем, Сеня на 4-ом.
17. Ира, Таня, Коля, Митя собирали ягоды. Таня собрала ягод больше каждого из детей, Ира - не меньше одного из мальчиков. Верно ли, что девочки собрали ягод больше, чем мальчики?
Ответ: Да, верно.
18. Найдите разность наименьшего пятизначного и наибольшего четырехзначного чисел.
Ответ:1.
Слайд 14
19.Из трёх одинаковых по виду колец одно несколько легче других.
Ответ: Кладём 2 кольца на весы. Если весы в равновесии, то оставшееся кольцо более лёгкое; если же одно кольцо перевисело, то ответ ясен.
20. «ПРИЗОВОЙ»
Мышке до норки по прямой 20 шагов. Кошке до мышки по той же прямой 5 прыжков. Пока кошка совершит 1 прыжок, мышка сделает 3 шага. 1 кошачий прыжок равен по длине 10-ти мышиным шагам. Мышка находится на прямой между кошкой и норкой. Догонит ли кошка мышку?
Ответ: Не догонит.
Слайд 15
21.Сколькими способами можно представить число 50 в виде суммы двух
Ответ: 50=2+48=4+46=...=46+4=48+2, всего 24 представления; считая а+b и b+а совпадающими, получим 12 способов.
22.Сколькими способами можно представить число 10 в виде суммы четырёх нечётных цифр? (Представления, различающиеся порядком слагаемых, считать совпадающими.)
Ответ: 3 способа, 10=1+1+1+7=1+1+3+5=1+3+3+3.
23. Сколькими способами можно представить число 6 в виде суммы нечётных слагаемых? (Представления, различающиеся порядком слагаемых, считать совпадающими.)
Ответ:4способа, 6=1+1+1+1+1+1=1+1+1+3=1+5=3+3.
Слайд 16
24.В шахматном турнире 3-мя участниками всего было сыграно 6 партий.
Ответ: 4 партии.
25.Призовой. Найдите сумму первых ста натуральных чисел.
Ответ: 5050.
26.Я задумала число, отняла от него 9 и прибавила 4, получилось 5. Какое число я задумала?
Ответ: x-9+4=5, х=10.
27.Назовите фамилию автора школьного учебника математики.
Ответ: А.Г. Мордкович и И.И Зубарева
Слайд 17
28.Выписаны все числа подряд от 1 до 99. Сколько раз
Ответ: 20 раз.
29.Сколько дырок окажется в клеёнке, если во время обеда 12 раз проткнуть
её вилкой с 4-мя зубчиками?
Ответ: 48 дырок.
30.«ПРИЗОВОЙ»
Кусок провода длиной 102 см надо разрезать на части длиной 15 см и 12 см, но так, чтобы не было остатков. Как это сделать ? Сколько решений имеет задача?
Ответ: 120=12+6*15=6*12+2*15, 2 решения.
Слайд 18
31.Напишите наименьшее десятизначное число, у которого все цифры различны.
Ответ: 1023456789.
32.Напишите
Ответ: 9876543210.
33.Сумма и произведение четырёх целых (не обязательно различных) чисел равна 8. Что это за числа?
Ответ: 8=4+2+1+1=4 . 2 . 1 . 1.
34. Во сколько раз 1м больше 1мм?
Ответ: 1000.
35. Призовой. Запишите число 100 девятью последовательными различными цифрами, соединёнными знаками действий.
Ответ: 100=1+2+3+4+5+6+7+8*9.
Слайд 19
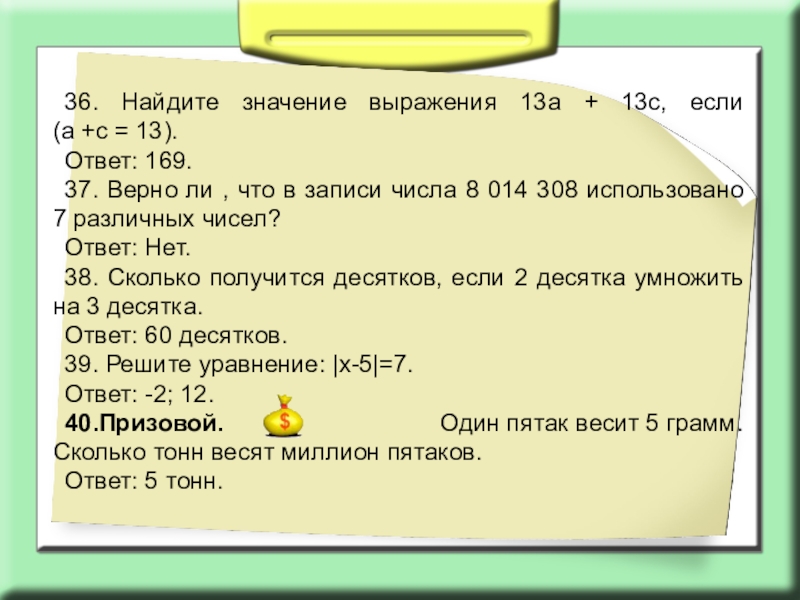
36. Найдите значение выражения 13а + 13с, если
Ответ: 169.
37. Верно ли , что в записи числа 8 014 308 использовано 7 различных чисел?
Ответ: Нет.
38. Сколько получится десятков, если 2 десятка умножить на 3 десятка.
Ответ: 60 десятков.
39. Решите уравнение: |х-5|=7.
Ответ: -2; 12.
40.Призовой. Один пятак весит 5 грамм. Сколько тонн весят миллион пятаков.
Ответ: 5 тонн.
Слайд 20
Ипподром.
Это оригинальная игра состоит из 5 заездов,
Тотализатор
Слайд 21
Первый заезд : «Скачки с препятствиями».
Участникам предлагается дать ответ на
1) вычислите 2+2 . 2-4:2+1
2) восстановите стёртые цифры (одной точкой обозначена одна цифра)
5..683<506..1
3) какое наименьшее целое положительное число вы можете записать двумя цифрами?
4) в семье 6 дочерей, каждая имеет брата. Сколько всего детей в семье?
5) бревно пилят на 10 частей. Сколько надо сделать распилов?
Свои ответы участники записывают на заранее заготовленных шаблонах, что позволяет ведущему быстро проверить ответы и определить призёра.
Слайд 22
Второй заезд: «Математический алфавит».
Выбирается одна из букв русского алфавита.
Слайд 23
Участникам заезда раздаются двухцветные сигнальные карточки. Ведущий зачитывает слова. После
Примерный набор слов: треугольник, ишак, уравнение, дециметр, дифирамб, периметр, пергамент, градус, формуляр, угол, интрига, резус, площадь, парк, задача, правило, прямоугольник, параллелепипед, кирпич, ребро, грань, вершина, верхушка, цифра, число, часы, частное, чемпион, произведение, сумма, слагаемое, слог, решение, размер.
Третий заезд : «Скачка с выбыванием».
Слайд 24
Четвёртый заезд: «Составь слово».
Участникам этого заезда предлагается достаточно длинное
Слова для четвёртого заезда: треугольник, уравнение, биссектриса, определение, прямоугольник, параллелепипед, координата.
Слайд 25Ведущий или ассистент записывает на бумаге трёхзначное число и демонстрирует его
Участники заезда должны отгадать, что записано.
Они по очереди называют свои варианты, а ведущий направляет их подсказками: больше, меньше.
Выигрывает заезд тот, кто первым угадает записанное число.
Аналогично разыгрывается второе место.
Расчёты со зрителями проводятся по окончании всех заездов, таким образом: если игрок, на которого была сделана ставка, занял первое место в заезде, то поставивший получает сумму ставки в «гениях», если второе место – в «талантах».
Пятый заезд: «Угадай число»
Слайд 26 Как и на любом аукционе, вход платный (цена 2 «таланта»).
На торги выставляются 8 лотов. Каждый лот, представляющий собой приз в 3 «гения», разыгрывался следующим образом.
Ведущий задаёт вопрос, предполагающий несколько ответов. Участники аукциона дают свои ответы. Выигрывает тот, чей ответ оказался последним.
Аукцион
Слайд 27Назовите пословицы и поговорки, в которых используются числительные.
Назовите меры веса.
Назовите меры
Назовите меры площади.
Назовите меры веса объёма.
Какие бывают дроби?
Приведите названия книг, в которых упоминаются числа.
Какие вы знаете геометрические фигуры?
Вопросы для аукциона
Слайд 29Альхова З.Н., Макеева А.В. «Внеклассная работа по математике»
Журнал «Математика в школе»
В. Ю. Сафонова. «Задачи по математике для внеклассной работы 5-6 классах».
П. И. Сорокин. «Занимательные задачи по математике».
Л. В. Гончарова «Предметные недели в школе. Математика».
Работа учителя математики ГБОУ лицей № 1571 г. Москвы Шеленковой Н.А.
Использованная литература: