- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентационный материал Теория натуральных чисел
Содержание
- 1. Презентационный материал Теория натуральных чисел
- 2. N числоРезультат счетаКоличественная теорияРезультат измерения величиныКоторый по счету?Аксиоматическая теория
- 3. Аксиоматическая теорияПравила аксиоматического построения математической теории:некоторые понятия
- 4. Если построение теории осуществляется аксиоматическим методом, то говорят, что теория построена дедуктивно.
- 5. Требования к системе аксиомНепротиворечивость (нельзя логическим путем
- 6. Аксиомы ПеаноАксиома 1. В множестве N существует
- 7. ММИ Если утверждение A(n) с натуральной
- 8. Сложение По правила построения аксиоматической теории,
- 9. Свойства сложения
- 10. Законы сложенияСочетательный закон (ассоциативный) ( а
- 11. Умножение Умножение натуральных чисел – алгебраическая операция, обладающая двумя свойствами:
- 12. Законы умноженияПравый дистрибутивный закон относительно сложения( а
- 13. Законы умноженияСочетательный закон (ассоциативный) ( а
- 14. ВычитаниеПравило вычитание числа из суммы( а +
- 15. Деление Делением натуральных чисел a и
- 16. ДелениеПравило деления суммы на число( а +в
- 17. Количественная теорияХарактеристику количества можно рассматривать как: число
- 18. Сложение С теоретико-множественных позиций сумма натуральных
- 19. Слайд 19
- 20. У маши было 3 яблока, у Пети
- 21. Натуральное число как мера величины Натуральное
- 22. Натуральное число как мера величиныЗадача на умножение:
- 23. Задача на деление: 12 л
N числоРезультат счетаКоличественная теорияРезультат измерения величиныКоторый по счету?Аксиоматическая теория
Слайд 2
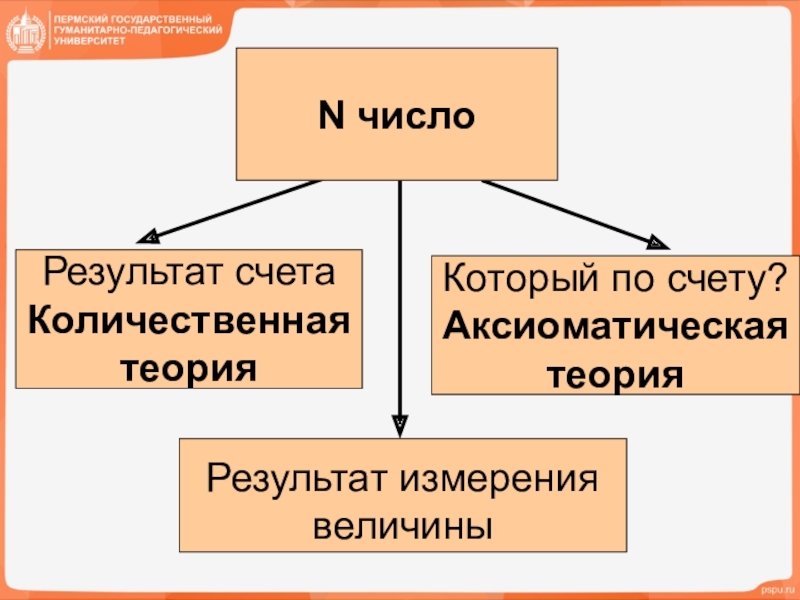
N число
Результат счета
Количественная
теория
Результат измерения
величины
Который по счету?
Аксиоматическая
теория
Слайд 3Аксиоматическая теория
Правила аксиоматического построения математической теории:
некоторые понятия теории выбираются в качестве
основных и принимаются без определения;
каждому понятию теории, которое не содержится в списке основных, дается определение, в нем разъясняется его смысл с помощью основных и предшествующих данному понятий;
формулируются аксиомы – предложения, которые в данной теории принимаются без доказательства; в них раскрываются свойства основных понятий;
каждое предложение теории, которое не содержится в списке аксиом, должно быть доказано; такие предложения называются теоремами и доказываются на основе аксиом и теорем, предшествующих рассматриваемой.
каждому понятию теории, которое не содержится в списке основных, дается определение, в нем разъясняется его смысл с помощью основных и предшествующих данному понятий;
формулируются аксиомы – предложения, которые в данной теории принимаются без доказательства; в них раскрываются свойства основных понятий;
каждое предложение теории, которое не содержится в списке аксиом, должно быть доказано; такие предложения называются теоремами и доказываются на основе аксиом и теорем, предшествующих рассматриваемой.
Слайд 4 Если построение теории осуществляется аксиоматическим методом, то говорят, что
теория построена дедуктивно.
Слайд 5Требования к системе аксиом
Непротиворечивость (нельзя логическим путем вывести два взаимно исключающих
друг друга предложения)
Полнота ( можно доказать)
Независимость (никакая из аксиом этой системы не является следствием других аксиом этой системы )
Полнота ( можно доказать)
Независимость (никакая из аксиом этой системы не является следствием других аксиом этой системы )
Слайд 6Аксиомы Пеано
Аксиома 1. В множестве N существует элемент, непосредственно не следующий
ни за каким элементом этого множества. Будем называть его единицей и обозначать символом 1.
Аксиома 2. Для каждого элемента a из N существует единственный элемент a', непосредственно следующий за a.
Аксиома 3. Для каждого элемента a из N существует не более одного элемента, за которым непосредственно следует a.
Аксиома 4. Всякое подмножество M множества N совпадает с N, если обладает свойствами: 1) а содержится в M; 2) из того что a содержится в M, следует, что и a’ содержится в M.
Аксиома 2. Для каждого элемента a из N существует единственный элемент a', непосредственно следующий за a.
Аксиома 3. Для каждого элемента a из N существует не более одного элемента, за которым непосредственно следует a.
Аксиома 4. Всякое подмножество M множества N совпадает с N, если обладает свойствами: 1) а содержится в M; 2) из того что a содержится в M, следует, что и a’ содержится в M.
Слайд 7ММИ
Если утверждение A(n) с натуральной переменной n истинно для
n=1 и из того, что оно истинно для n=k (k – произвольное натуральное число), следует, что оно истинно и для следующего числа n=k’, то утверждение A(n) истинно для любого натурального числа n. Метод доказательства основанный на этой теореме называется метод математической индукции
Слайд 8Сложение
По правила построения аксиоматической теории, определение сложения натуральных чисел
нужно ввести, используя только отношение «непосредственно», и понятия «натуральное число» и «предшествующее число».
Слайд 10Законы сложения
Сочетательный закон
(ассоциативный)
( а + в )
+ с = а + (в + с)
Коммутативный закон (переместительный)
( а + в )= (в + а)
Коммутативный закон (переместительный)
( а + в )= (в + а)
Слайд 11Умножение
Умножение натуральных чисел – алгебраическая операция, обладающая двумя свойствами:
Слайд 12Законы умножения
Правый дистрибутивный закон относительно сложения
( а + в ) *
с = а *с + в * с
Левый дистрибутивный закон относительно сложения
а * (в + с) = а * в + а* с
Левый дистрибутивный закон относительно сложения
а * (в + с) = а * в + а* с
Слайд 13Законы умножения
Сочетательный закон
(ассоциативный)
( а * в )
* с = а * (в * с)
Коммутативный закон (переместительный)
( а * в )= (в * а)
Коммутативный закон (переместительный)
( а * в )= (в * а)
Слайд 14Вычитание
Правило вычитание числа из суммы
( а + в ) - с
= ( а – с ) + в = а + ( в – с)
Правило вычитания суммы из числа
а – ( в + с) = ( а – в ) – с = ( а – с) – в
Правило вычитания суммы из числа
а – ( в + с) = ( а – в ) – с = ( а – с) – в
Слайд 15Деление
Делением натуральных чисел a и b называется операция, удовлетворяющая
условию: a ÷ b = c тогда и только тогда, когда b ∙ c = a.
Слайд 16Деление
Правило деления суммы на число
( а +в ) : с =
а : с + в : с
Правило деления разности на число
( а - в ) : с = а : с - в : с , если в < а
Правило деления произведения на число
( а * в ) : с = а * ( в : с) = ( а : с ) : в
Правило деления числа на сумму
а : ( в * с) = (а : в ) : с = (а : с) : в
Правило деления разности на число
( а - в ) : с = а : с - в : с , если в < а
Правило деления произведения на число
( а * в ) : с = а * ( в : с) = ( а : с ) : в
Правило деления числа на сумму
а : ( в * с) = (а : в ) : с = (а : с) : в
Слайд 17Количественная теория
Характеристику количества можно рассматривать как:
число элементов в множестве А,
получаемое при счете, т.е. а = n(А)
общее свойство класса конечных равномощных множеств
общее свойство класса конечных равномощных множеств
Слайд 18Сложение
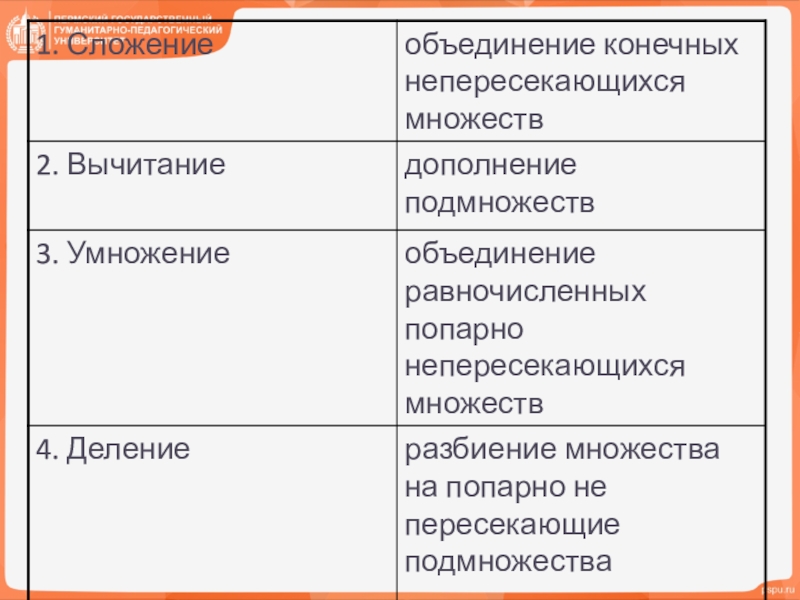
С теоретико-множественных позиций сумма натуральных чисел а и b
представляет собой число элементов в объединении конечных непересекающихся множеств А и В таких, что a= n(А), b=n(В):
a+ b = n(А) + n(В) = n(А B), если А В =
a+ b = n(А) + n(В) = n(А B), если А В =
Слайд 20У маши было 3 яблока, у Пети 2 яблока. Сколько число
элементов в объединении?
У маши 6 яблок. У Кати на 2 яблока меньше. Сколько у Кати яблок?
У трех детей по 5 яблок. Сколько всего яблок?
12 яблок раздали 3 детям поровну. Сколько яблок досталось каждому.
У маши 6 яблок. У Кати на 2 яблока меньше. Сколько у Кати яблок?
У трех детей по 5 яблок. Сколько всего яблок?
12 яблок раздали 3 детям поровну. Сколько яблок досталось каждому.
Слайд 21Натуральное число как мера величины
Натуральное число - число, которое
показывает, из скольких единичных отрезков состоит отрезок, длина которого измеряется.
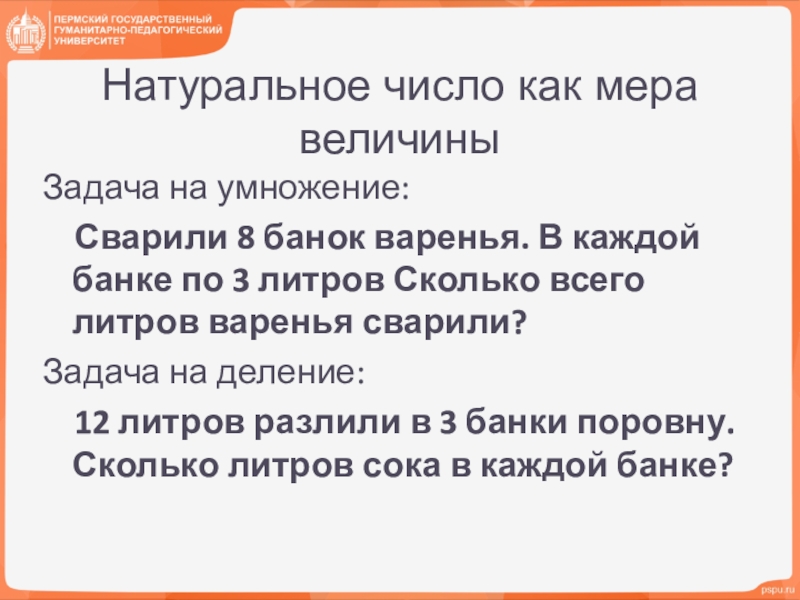
Слайд 22Натуральное число как мера величины
Задача на умножение:
Сварили 8 банок
варенья. В каждой банке по 3 литров Сколько всего литров варенья сварили?
Задача на деление:
12 литров разлили в 3 банки поровну. Сколько литров сока в каждой банке?
Задача на деление:
12 литров разлили в 3 банки поровну. Сколько литров сока в каждой банке?
Слайд 23Задача на деление:
12 л сока разлили по 3
литра в банка. Сколько получилось банок?
Задача на сложение:
В корзине 2 кг яблок , 3 кг груш. Сколько всего?
Задача на вычитание:
В корзине 5 кг. Съели 3 кг. Сколько осталось?
Задача на сложение:
В корзине 2 кг яблок , 3 кг груш. Сколько всего?
Задача на вычитание:
В корзине 5 кг. Съели 3 кг. Сколько осталось?