Презентация, доклад на тему Повторение геометрии при подготовке к ОГЭ

тематическому принципу:

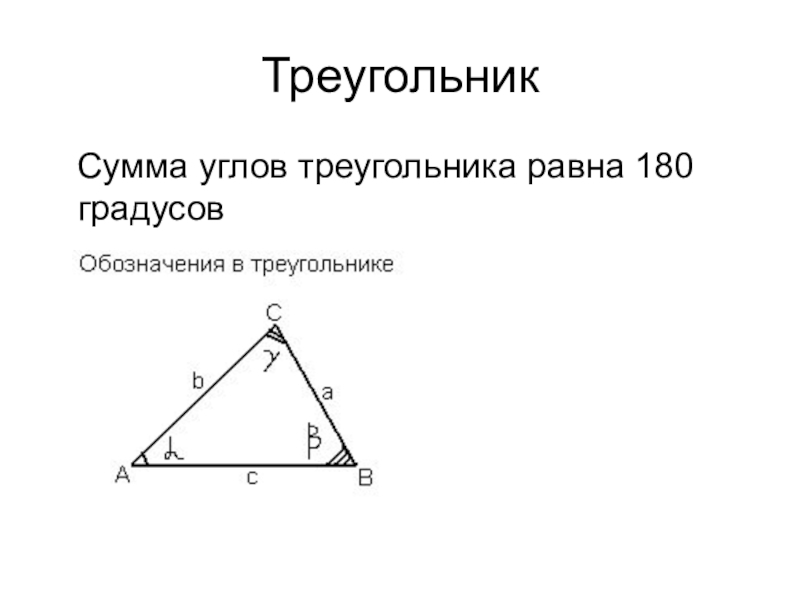
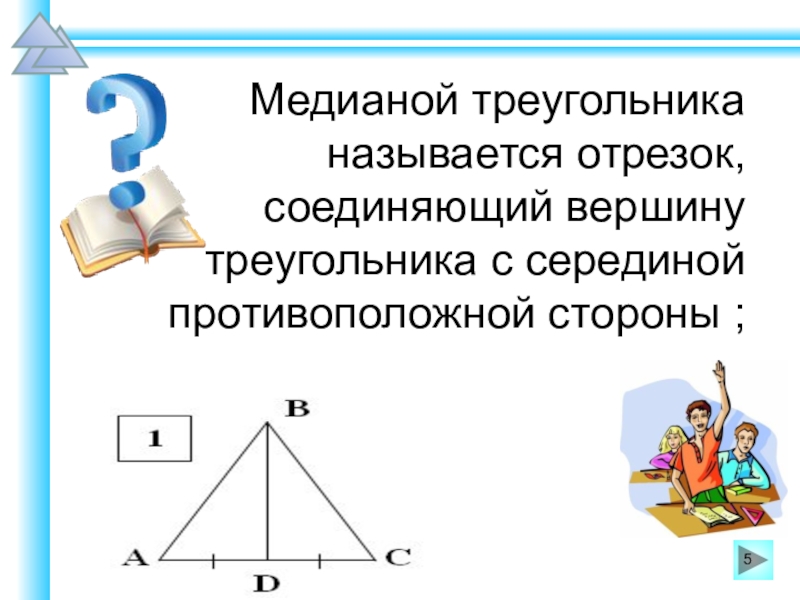
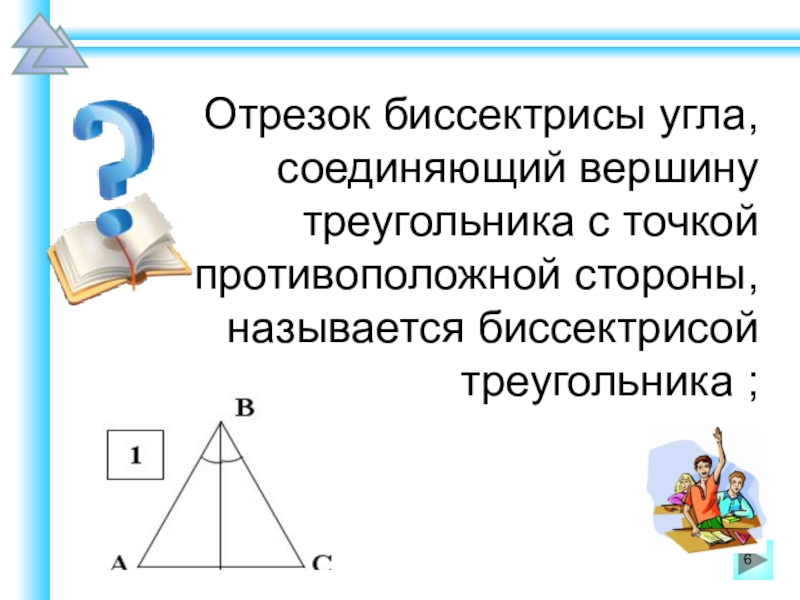
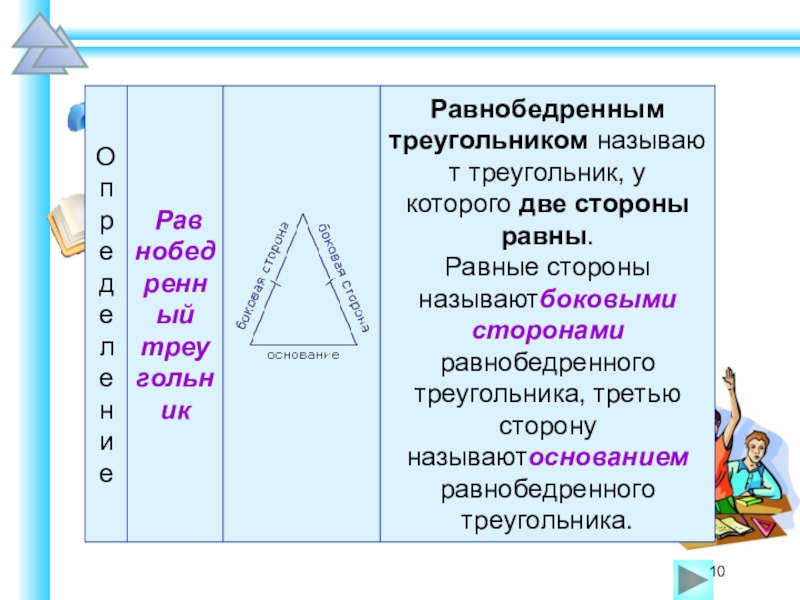
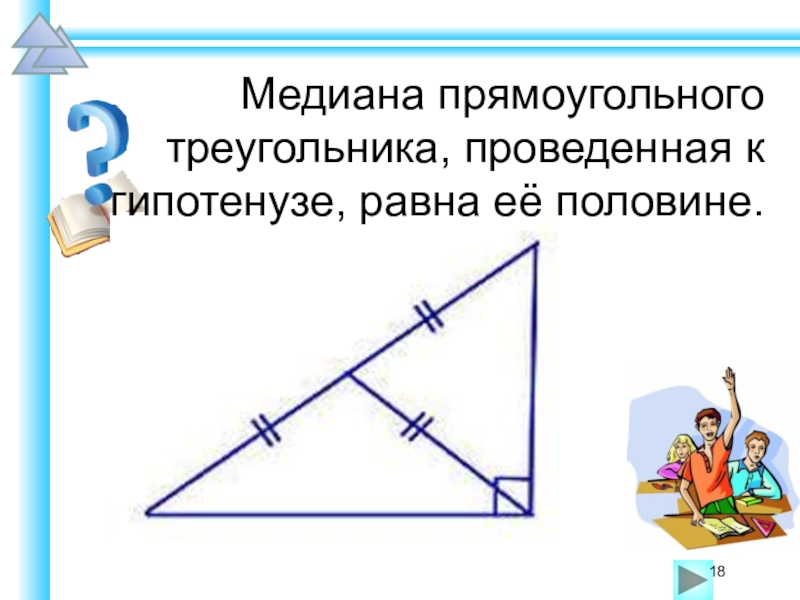
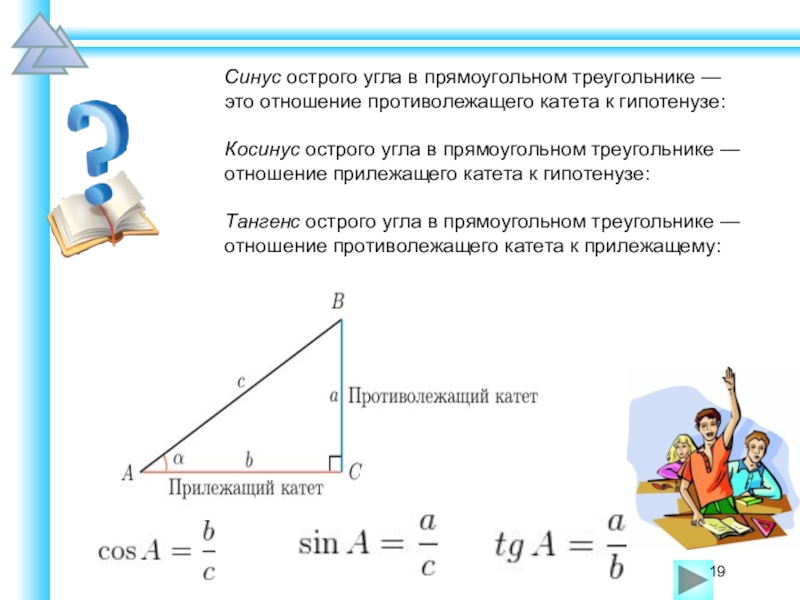
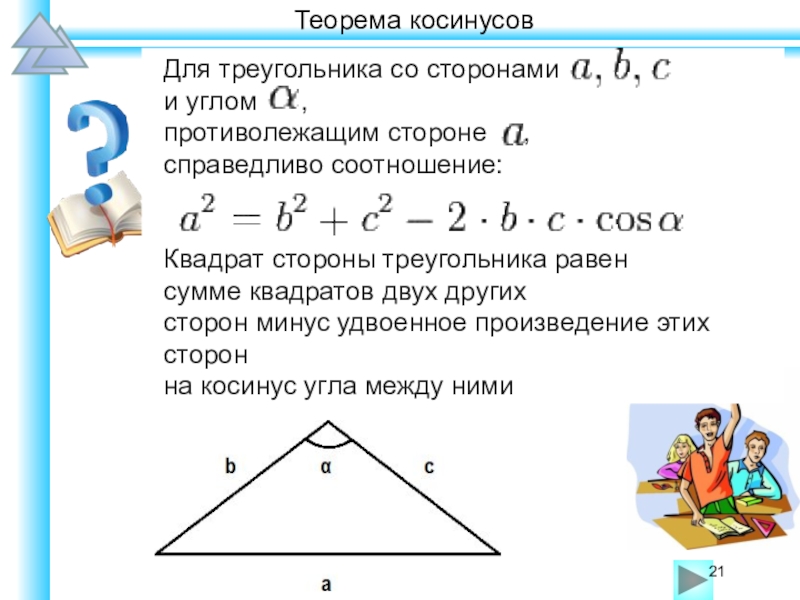
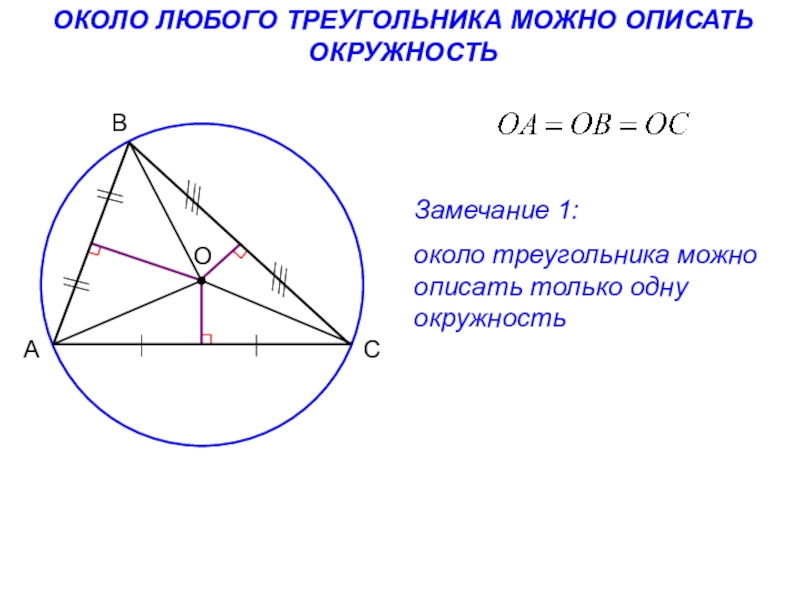
Не следует стараться решить как можно больше вариантов заданий предыдущих лет. Запомнить все решения всех заданий невозможно, поэтому разумнее учить школьников общим универсальным приёмам и подходам к решению задач соответствующих типов.

- Очень эффективен приём показа учителем мысленного поиска способа решения задачи:
Учитель должен быть готов раскрыть перед учащимися ход своих мыслей

Хороший результат получается, когда учитель инсценирует «тупик» в процессе решения задачи:
в этом случае дети должны уметь найти место, с которого пошёл «тупиковый» вариант, чтобы, вернувшись к нему, найти другой вариант решения.

на уроках заключительного повторения:

высота, биссектриса, серединный перпендикуляр к стороне…).
Вписанная и описанная окружности.
Тригонометрические функции острого угла прямоугольного треугольника.
Теорема синусов.
Теорема косинусов.
Теорема Пифагора.
Виды четырехугольников. Свойства и признаки параллелограмма, прямоугольника, ромба, квадрата и трапеции.
Формулы площадей плоских фигур.

;

называется биссектрисой треугольника ;

называется высотой треугольника.

Средняя линия параллельна одной из сторон треугольника и равна её половине

два других угла
в сумме дают 900.
                                                                                             

катеты треугольника равны

в прямоугольном треугольнике —
отношение прилежащего катета к гипотенузе:
                      
Тангенс острого угла в прямоугольном треугольнике —
отношение противолежащего катета к прилежащему:
                    

соотношение:

                                                                
Квадрат стороны треугольника равен
сумме квадратов двух других
сторон минус удвоенное произведение этих сторон
на косинус угла между ними

Теорема косинусов

одну окружность

О

СУММА ПРОТИВОПОЛОЖНЫХ УГЛОВ РАВНА 180О

ЕСЛИ СУММА ПРОТИВОПОЛОЖНЫХ УГЛОВ ЧЕТЫРЕХУГОЛЬНИКА РАВНА 180О, ТО ОКОЛО НЕГО МОЖНО ОПИСАТЬ ОКРУЖНОСТЬ

D

A

C

B

– точка пересечения
биссектрис треугольника.

мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;

числе: для углов от 0 до 180° определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
6. решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;

7. использовать приобретенные знания и умения в практической деятельности и повседневной жизни

получения удовлетворительной оценки, например, в качестве заданий для самопроверки достижения обязательной подготовки