- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Начальные геометрические сведения
Содержание
- 1. Начальные геометрические сведения
- 2. Цель: привести в систему знания, умения, навыки по теме; совершенствовать навыки решения задач.
- 3. «Никогда до настоящего времени мы не жили
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Храм преп. Серафима Саровского на улице Лёкурб
- 8. Проверка домашнего заданияВопросы к главе I (1-21)
- 9. Условия работы в группах Класс делится на
- 10. Решение задач по готовым чертежамКо всем задачам
- 11. Задача 1.Дано: АВ : ВС = 4
- 12. Задача 2Дано: СВ на 3 см меньше,
- 13. Задача 3Длина отрезка АВ = 6 см.
- 14. Задача 4Дано ˂АОВ= 125°, ˂АОD = 31°,
- 15. Задача 5Дано: ˂ AOE =116°. Найти:˂BOD
- 16. Задача 6Дано: ˂1 : ˂2 = 4
- 17. Задача 7Дано: a∩dНайти: ˂ 1, ˂ 2
- 18. Заголовок слайдаТекст слайда
- 19. Заголовок слайдаТекст слайда
- 20. Заголовок слайдаТекст слайда
- 21. РефлексияТекст слайда
- 22. Домашнее задание
Цель: привести в систему знания, умения, навыки по теме; совершенствовать навыки решения задач.
Слайд 2Цель: привести в систему знания,
умения, навыки по теме; совершенствовать навыки
решения задач.
Слайд 3«Никогда до настоящего времени мы не жили в такой геометрический период.
Все вокруг – геометрия».
( Ле Корбюзье - французский архитектор ).
( Ле Корбюзье - французский архитектор ).
Слайд 7Храм преп. Серафима Саровского на улице Лёкурб в Париже
Этот удивительный храм
возник в 1933 году под началом протоиерея Димитрия Троицкого.
Изначально он представлял собой маленькую церквушку, ютившуюся в бывшем бараке во
дворе общежития русских студентов. В 1974 году архитектором Андреем Фёдоровым он
был частично перестроен , в таком виде храм действует и сейчас
Изначально он представлял собой маленькую церквушку, ютившуюся в бывшем бараке во
дворе общежития русских студентов. В 1974 году архитектором Андреем Фёдоровым он
был частично перестроен , в таком виде храм действует и сейчас
Слайд 9Условия работы в группах
Класс делится на три группы
1 группа
– Тульцов В., Сафронов Г., Гольченко А., Добычин А.
2 группа – Гришин Я, Калугин З., Снигур И., Пронин К.
3 группа – Елистратов В., Зырянов Д., Корчуганов А., Марков Л.
Перед тем как вытянуть одну из приготовленных карточек, капитан команды называет фамилию и имя члена команды, который будет отвечать. При этом отвечающие каждый раз должны быть разными.
Если назначенный ученик дал верный ответ на вопрос – команда получает 2 балла,
если нет – на помощь приходит команда, но в этом случае команде начисляется только 1 балл.
Если команда не смогла ответить, отвечает та команда, которая первая изъявила желание, и получает 1 балл.
Количество баллов, заработанных каждой командой, учитывается в оценочном листе.
Команде – победителю даётся право поставить членам своей команды по 2 пятёрки и 2 четвёрки в зависимости от количества баллов, набранных учащимися; команде, занявшей второе место – 1 пятёрку и 1четвёрку; команде, занявшей третье место – 2 четвёрки.
Подведение итогов по вопросам.
2 группа – Гришин Я, Калугин З., Снигур И., Пронин К.
3 группа – Елистратов В., Зырянов Д., Корчуганов А., Марков Л.
Перед тем как вытянуть одну из приготовленных карточек, капитан команды называет фамилию и имя члена команды, который будет отвечать. При этом отвечающие каждый раз должны быть разными.
Если назначенный ученик дал верный ответ на вопрос – команда получает 2 балла,
если нет – на помощь приходит команда, но в этом случае команде начисляется только 1 балл.
Если команда не смогла ответить, отвечает та команда, которая первая изъявила желание, и получает 1 балл.
Количество баллов, заработанных каждой командой, учитывается в оценочном листе.
Команде – победителю даётся право поставить членам своей команды по 2 пятёрки и 2 четвёрки в зависимости от количества баллов, набранных учащимися; команде, занявшей второе место – 1 пятёрку и 1четвёрку; команде, занявшей третье место – 2 четвёрки.
Подведение итогов по вопросам.
Слайд 10Решение задач по готовым чертежам
Ко всем задачам написать ответы в тетрадях,
рассуждения можно вести устно или на черновике.
Слайд 11Задача 1.
Дано:
АВ : ВС = 4 : 3,
АС =
21см.
Найти: АВ, ВС.
Найти: АВ, ВС.
Решение:
АС– 7 частей,21 : 7 = 3(см) на одну часть. АВ = 3 ×4 = 12см,
ВС = 3×3 = 9см.
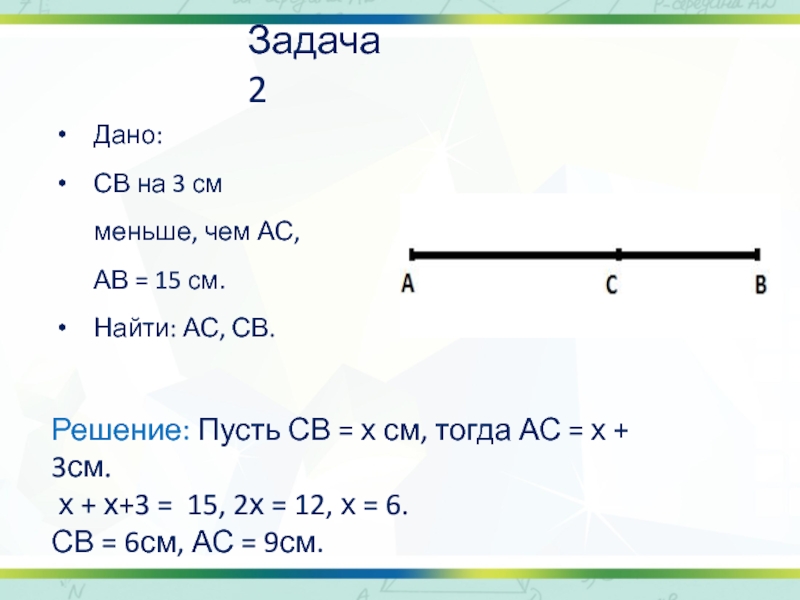
Слайд 12Задача 2
Дано:
СВ на 3 см меньше, чем АС, АВ =
15 см.
Найти: АС, СВ.
Найти: АС, СВ.
Решение: Пусть СВ = х см, тогда АС = х + 3см.
х + х+3 = 15, 2х = 12, х = 6.
СВ = 6см, АС = 9см.
Слайд 13Задача 3
Длина отрезка АВ = 6 см. М ϵ АВ. Найдите
длину отрезка ВМ, если:
а) АМ = 2ВМ;
б) 2ВМ + 3АМ = 14.
а) АМ = 2ВМ;
б) 2ВМ + 3АМ = 14.
Решение: М ϵ АВ, значит, АМ + МВ = АВ, АВ = 6см, следовательно, АМ + МВ = 6.
а) АМ = 2ВМ, тогда 2МВ + МВ = 6; МВ =2 см.
б) 2ВМ + 3АМ =14, тогда 2(АМ+ВМ)+АМ =14.
Т.к АМ+МВ=АВ=6, то 2∙6+АМ=14, АМ=2, ВМ=4см.
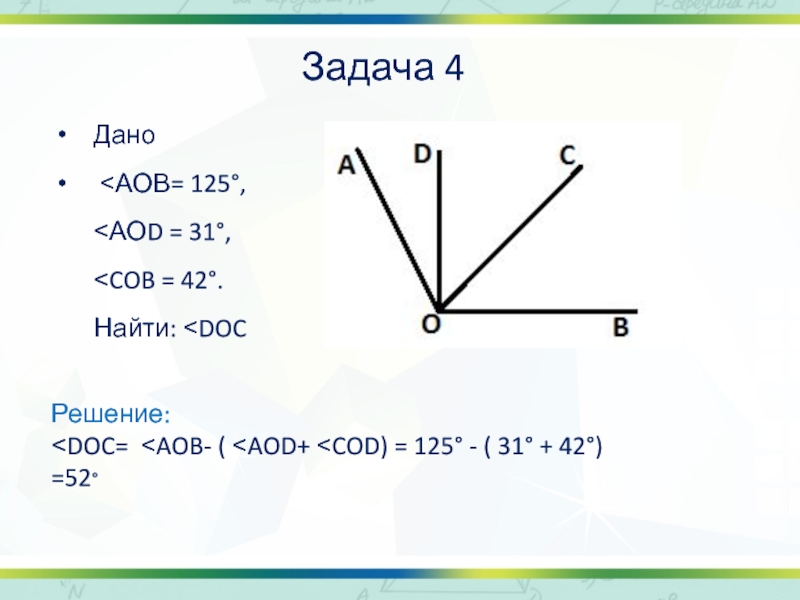
Слайд 14Задача 4
Дано
˂АОВ= 125°, ˂АОD = 31°, ˂COB = 42°.
Найти: ˂DOC
Решение:
˂DOC= ˂AOB- ( ˂AOD+ ˂COD) = 125° - ( 31° + 42°) =52°
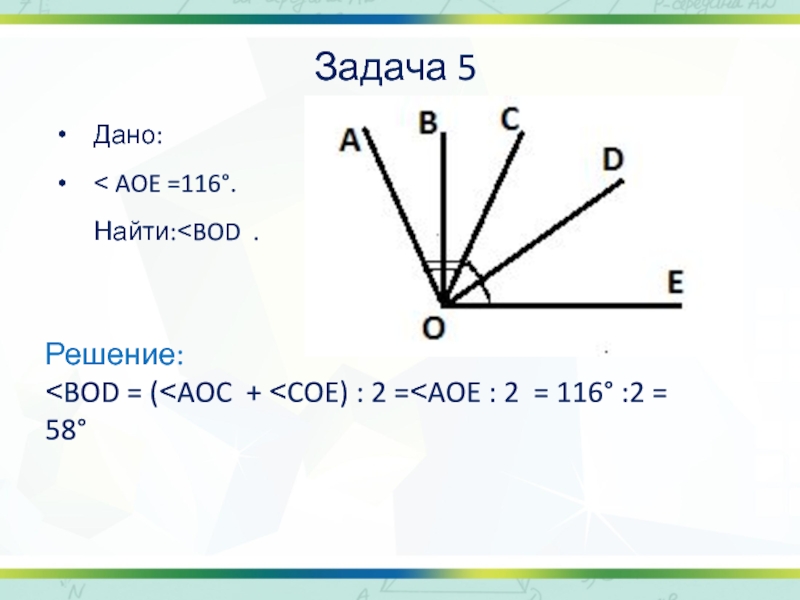
Слайд 15Задача 5
Дано:
˂ AOE =116°. Найти:˂BOD .
Решение:
˂BOD =
(˂AOC + ˂COE) : 2 =˂AOE : 2 = 116° :2 = 58°
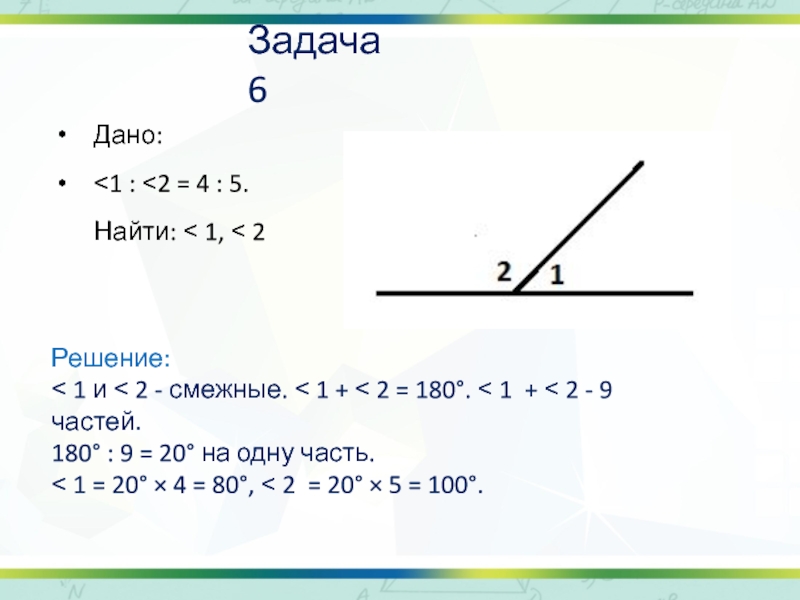
Слайд 16Задача 6
Дано:
˂1 : ˂2 = 4 : 5. Найти: ˂
1, ˂ 2
Решение:
˂ 1 и ˂ 2 - смежные. ˂ 1 + ˂ 2 = 180°. ˂ 1 + ˂ 2 - 9 частей.
180° : 9 = 20° на одну часть.
˂ 1 = 20° × 4 = 80°, ˂ 2 = 20° × 5 = 100°.
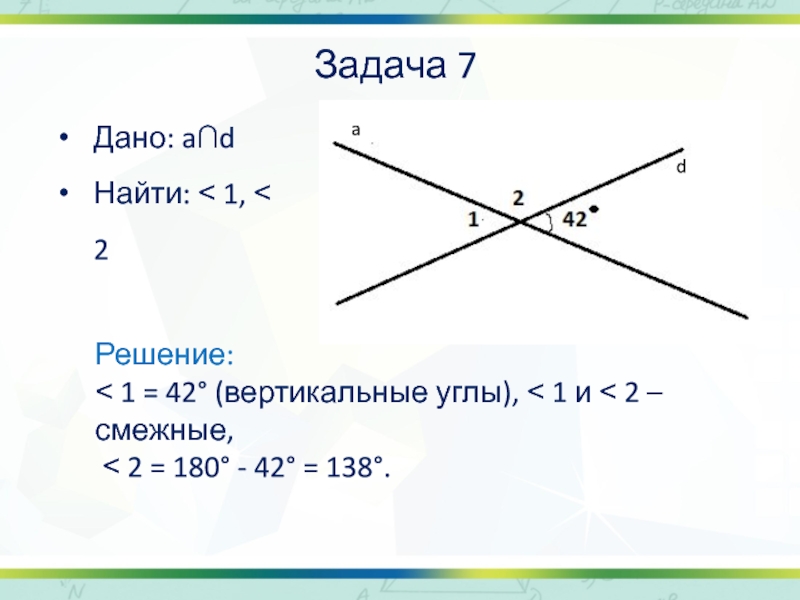
Слайд 17Задача 7
Дано: a∩d
Найти: ˂ 1, ˂ 2
a
d
Решение:
˂ 1
= 42° (вертикальные углы), ˂ 1 и ˂ 2 – смежные,
˂ 2 = 180° - 42° = 138°.
˂ 2 = 180° - 42° = 138°.
Слайд 22Домашнее задание
Повторить главу II
(§1, 2, 3 без доказательств),
вопросы 1-15.
Решить задачи № 324, 327.
вопросы 1-15.
Решить задачи № 324, 327.
