высшей категории
МОУ «Горячеключевская СОШ»
Омского района Омской области
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Метод координат при решении стереометрических задач ЕГЭ
Содержание
- 1. Метод координат при решении стереометрических задач ЕГЭ
- 2. Немного из истории координатного метода
- 3. Суть метода координат Сущность метода координат как
- 4. Цели изучения метода координат показать учащимся эффективность
- 5. Главное преимущество метода координатРешение задач С2 ЕГЭ-2010
- 6. Основные виды задач С2 ЕГЭ - 2010Угол
- 7. Причины трудностей учащихся при решении подобных задачОтсутствие
- 8. Слайд 8
- 9. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ Задача. В
- 10. Алгоритм решения задачи: 1.Ввести прямоугольную систему координат2.Ввести
- 11. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИЗадача. В правильной шестиугольной
- 12. Алгоритм решения задачи:1.Ввести прямоугольную систему координат2.Рассмотреть правильный
- 13. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮЗадача. В кубе
- 14. Алгоритм решения задачи:1.Ввести прямоугольную систему координат2.Ввести направляющий
- 15. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ Задача. В
- 16. Алгоритм решения задачи:1.Ввести прямоугольную систему координат, определить
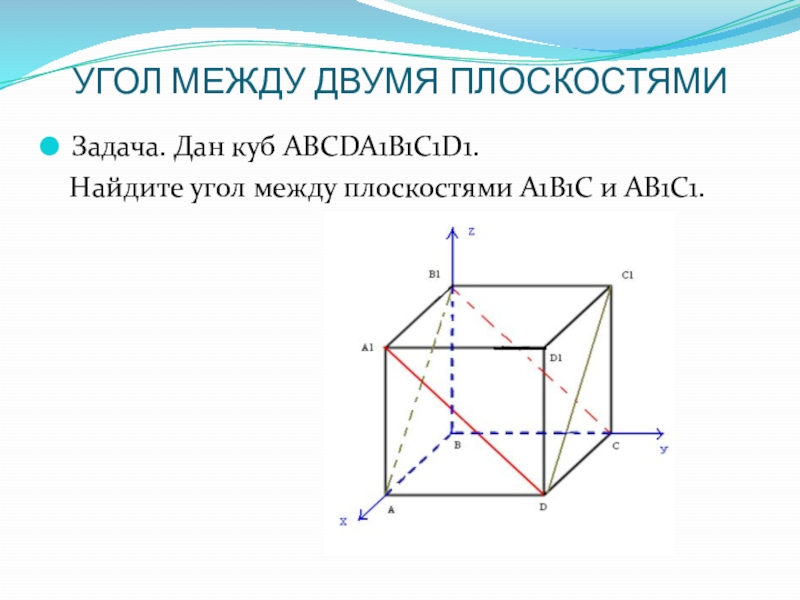
- 17. УГОЛ МЕЖДУ ДВУМЯ ПЛОСКОСТЯМИ Задача. Дан куб
- 18. Алгоритм решения задачи:1.Ввести прямоугольную систему координат. 2.
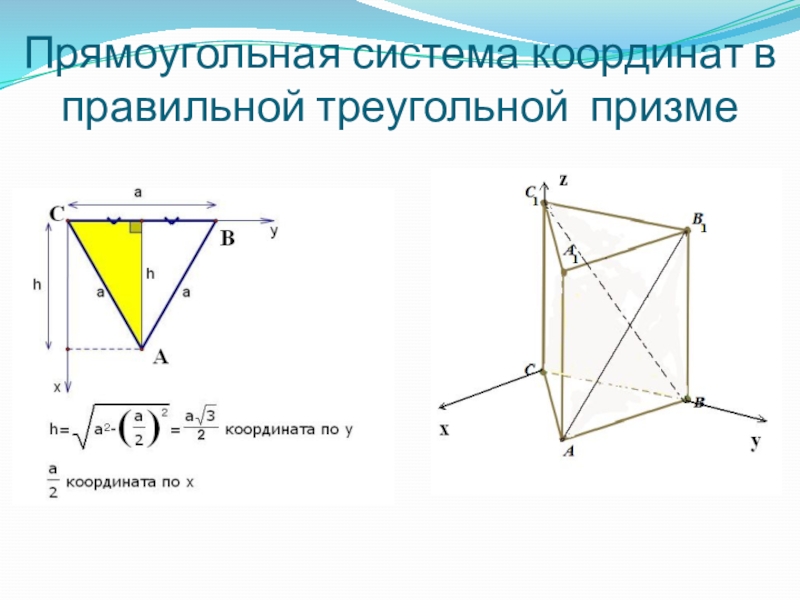
- 19. Прямоугольная система координат в правильной треугольной призме
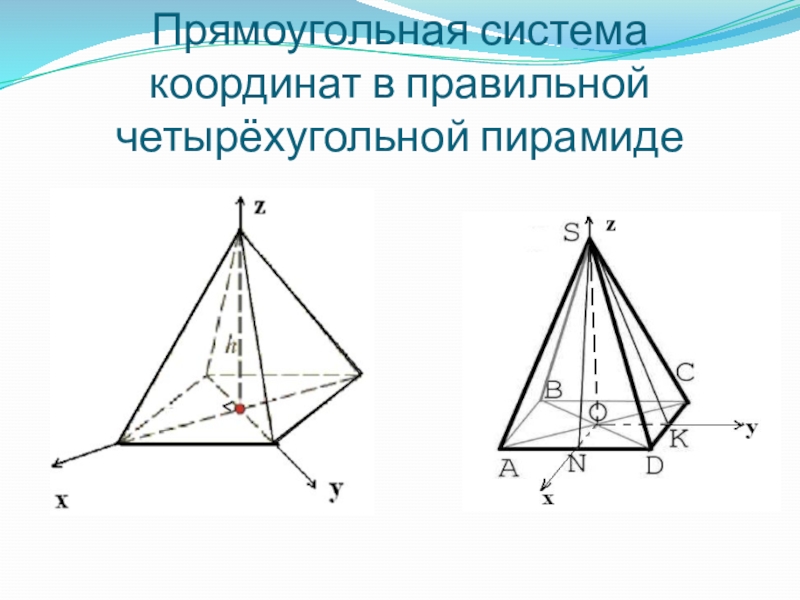
- 20. Прямоугольная система координат в правильной четырёхугольной пирамиде
- 21. Учебник «Геометрия 10-11», Л.С.Атанасян, В.Ф.Бутузов и др.В издание 2010 г.введён п.53 Уравнение плоскости
- 22. Метод координат, его плюсы и минусыИзбавляет от
- 23. Желаю успехов в выборе. Спасибо за внимание!
Немного из истории координатного метода Название «декартовы координаты» наводит на ложную мысль о том, что эти координаты были открыты Декартом. В действительности прямоугольные координаты использовались в геометрии еще до нашей эры. Декарт внес в
Слайд 2
Немного из истории координатного метода
Название «декартовы координаты» наводит на
ложную мысль о том, что эти координаты были открыты Декартом. В действительности прямоугольные координаты использовались в геометрии еще до нашей эры.
Декарт внес в прямоугольные координаты очень важное усовершенствование, введя правила выбора знаков. Но главное, пользуясь прямоугольными координатами, он построил аналитическую геометрию на плоскости, связав этим геометрию и алгебру.
Декарт внес в прямоугольные координаты очень важное усовершенствование, введя правила выбора знаков. Но главное, пользуясь прямоугольными координатами, он построил аналитическую геометрию на плоскости, связав этим геометрию и алгебру.
Слайд 3Суть метода координат
Сущность метода координат как метода решения задач состоит в
том, что, выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Обратно, пользуясь координатами, можно применять геометрию к решению алгебраических задач.
Метод координат обеспечивает тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.
В некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрическими способами.
Метод координат связан с одной геометрической сложностью. Одна и та же задача получает различное аналитическое представление в зависимости от того или иного выбора системы координат.
Метод координат обеспечивает тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.
В некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрическими способами.
Метод координат связан с одной геометрической сложностью. Одна и та же задача получает различное аналитическое представление в зависимости от того или иного выбора системы координат.
Слайд 4Цели изучения метода координат
показать учащимся эффективность метода решения задач и
доказательства ряда теорем;
показать на основе этого метода тесную связь алгебры и геометрии;
способствовать развитию вычислительной и графической культуры учащихся.
показать на основе этого метода тесную связь алгебры и геометрии;
способствовать развитию вычислительной и графической культуры учащихся.
Слайд 5Главное преимущество метода координат
Решение задач С2 ЕГЭ-2010 при помощи метода координат
алгоритмитизировано,
а значит становится более простым для учащихся.
а значит становится более простым для учащихся.
Слайд 6Основные виды задач С2 ЕГЭ - 2010
Угол между двумя прямыми
Угол между
прямой и плоскостью
Расстояние от точки до плоскости
Угол между двумя плоскостями
Расстояние от точки до плоскости
Угол между двумя плоскостями
Слайд 7Причины трудностей учащихся при решении подобных задач
Отсутствие пространственного воображения.
Сложность в усвоении
понятий: угла между скрещивающимися прямыми, угла между прямой и плоскостью, двугранного угла, линейного угла, взаимного расположения плоскостей.
Недостаток разнообразия такого типа задач в учебниках.
В школьной программе по математике методу координат уделяется сравнительно мало внимания.
Недостаток разнообразия такого типа задач в учебниках.
В школьной программе по математике методу координат уделяется сравнительно мало внимания.
Слайд 8
АЛГОРИТМЫ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ С2 ЕГЭ – 2010 (шпаргалка-помощница)
Все условия для знаний создаются вам сейчас,
До ЕГЭ ещё есть время,
но наступит этот час!
Так что нужно потрудиться,
изучить и закрепить,
Мой совет вам - не лениться,
а математику учить!
Н.В.Алфёрова
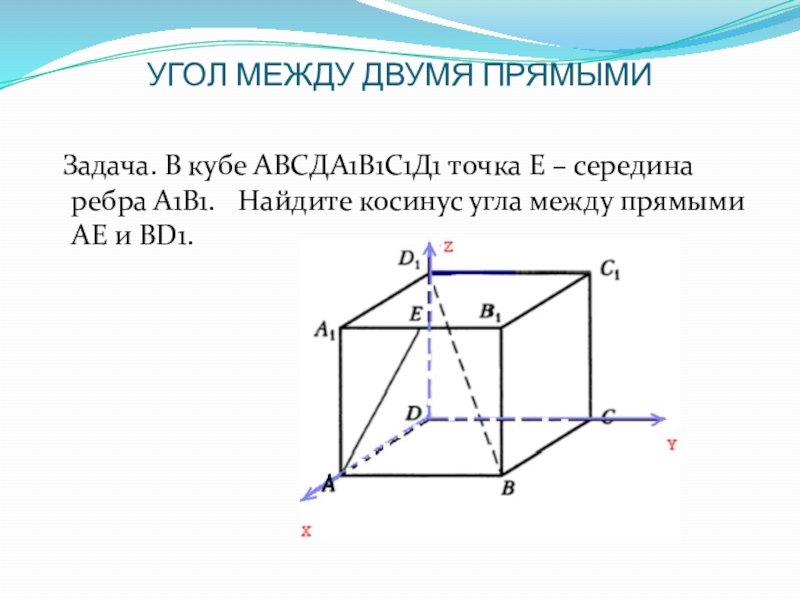
Слайд 9УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
Задача. В кубе АВСДА1В1С1Д1 точка Е –
середина ребра А1В1. Найдите косинус угла между прямыми АЕ и ВD1.
Слайд 10Алгоритм решения задачи:
1.Ввести прямоугольную систему координат
2.Ввести направляющие векторы данных прямых и
определить их координаты.
3. Найти косинус угла между векторами по формуле
сosα =
3. Найти косинус угла между векторами по формуле
сosα =
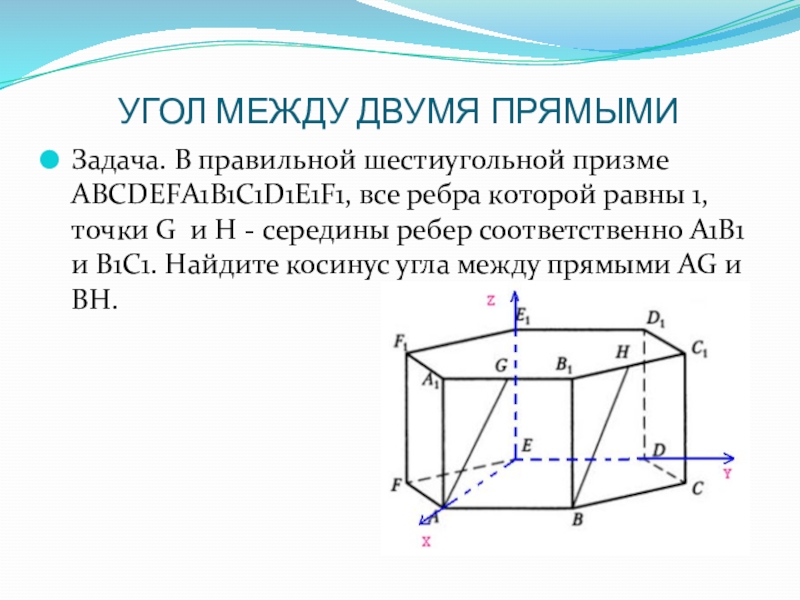
Слайд 11УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
Задача. В правильной шестиугольной призме АВСDEFА1В1С1D1E1F1, все ребра
которой равны 1, точки G и H - середины ребер соответственно А1В1 и В1С1. Найдите косинус угла между прямыми AG и BH.
Слайд 12Алгоритм решения задачи:
1.Ввести прямоугольную систему координат
2.Рассмотреть правильный шестиугольник на плоскости, вычислить
длину его диагонали АЕ по т. косинусов.
3.Ввести направляющие векторы данных прямых и
определить их координаты.
4.Найти косинус угла между векторами по формуле
сosα =
3.Ввести направляющие векторы данных прямых и
определить их координаты.
4.Найти косинус угла между векторами по формуле
сosα =
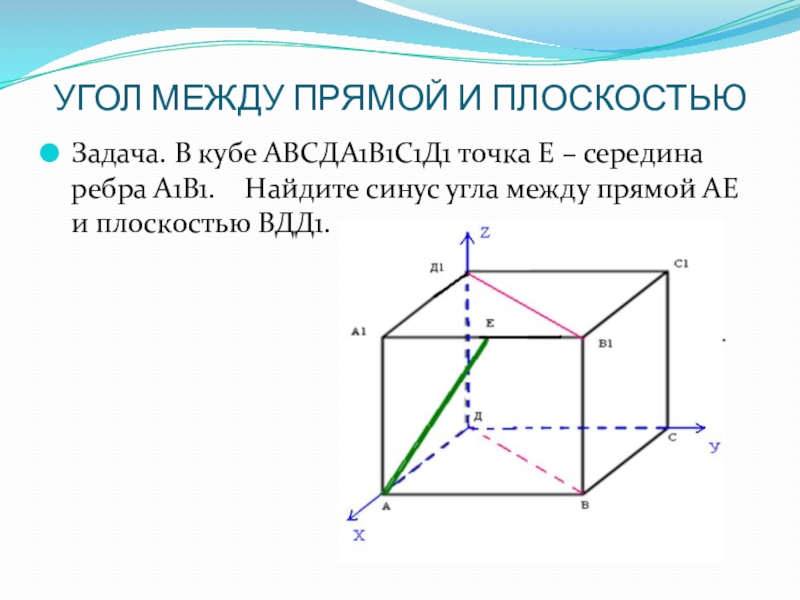
Слайд 13УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Задача. В кубе АBCДА1В1С1Д1 точка Е –
середина ребра А1В1. Найдите синус угла между прямой АЕ и плоскостью ВДД1.
Слайд 14Алгоритм решения задачи:
1.Ввести прямоугольную систему координат
2.Ввести направляющий вектор данной прямой,
определить его координаты: АЕ (х1;у1;z1)
3.Вывести уравнение плоскости: Ах+Ву+Сz+D=0, где N (A; В; С) – вектор нормали
4.Найти синус угла между векторами по формуле:
sinα =
3.Вывести уравнение плоскости: Ах+Ву+Сz+D=0, где N (A; В; С) – вектор нормали
4.Найти синус угла между векторами по формуле:
sinα =
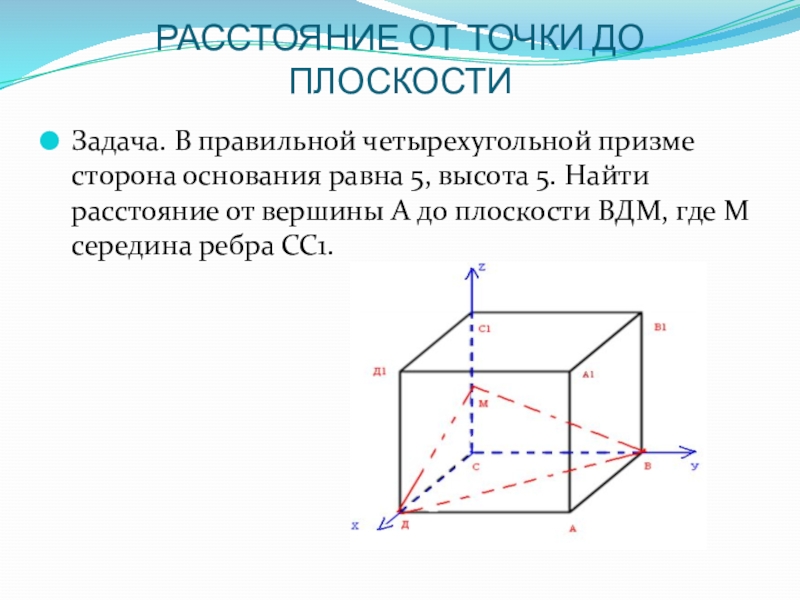
Слайд 15РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
Задача. В правильной четырехугольной призме сторона основания
равна 5, высота 5. Найти расстояние от вершины A до плоскости BДM, где M середина ребра CC1.
Слайд 16Алгоритм решения задачи:
1.Ввести прямоугольную систему координат, определить координаты данной точки A
(х0;у0;z0).
2. Вывести уравнение плоскости: Ах+Ву+Сz+D=0, где N (A; В; С) – вектор нормали
3.Найти расстояние от точки A (х0;у0;z0) до плоскости Ах+Ву+Сz+D=0 по формуле:
d =
2. Вывести уравнение плоскости: Ах+Ву+Сz+D=0, где N (A; В; С) – вектор нормали
3.Найти расстояние от точки A (х0;у0;z0) до плоскости Ах+Ву+Сz+D=0 по формуле:
d =
Слайд 17УГОЛ МЕЖДУ ДВУМЯ ПЛОСКОСТЯМИ
Задача. Дан куб АВСDA1B1C1D1.
Найдите угол между
плоскостями А1В1С и АВ1С1.
Слайд 18Алгоритм решения задачи:
1.Ввести прямоугольную систему координат.
2. Вывести уравнения плоскостей: А1х+В1у+С1z+D1=0,
где
N1 (A1; В1; С1) – вектор нормали одной плоскости,
А2х+В2у+С2z+D2=0, где N2(A2; В2; С2) – вектор нормали второй плоскости.
3.Вычислите косинус угла между плоскостями по формуле: сosα = | |
N1 (A1; В1; С1) – вектор нормали одной плоскости,
А2х+В2у+С2z+D2=0, где N2(A2; В2; С2) – вектор нормали второй плоскости.
3.Вычислите косинус угла между плоскостями по формуле: сosα = | |
Слайд 21Учебник «Геометрия 10-11»,
Л.С.Атанасян, В.Ф.Бутузов и др.
В издание 2010 г.
введён п.53
Уравнение плоскости
Слайд 22Метод координат, его плюсы и минусы
Избавляет от необходимости прибегать к наглядному
представлению сложных пространственных изображений. +
При решении не нужна высокая степень сообразительности, что негативно сказывается на творческих способностях учащихся. -
Одна и та же задача получает различное аналитическое представление в зависимости от того или иного выбора системы координат. -
Нацелен на результат ЕГЭ, т.е. в рамках учебного времени, даёт возможность «натаскивания» учащихся на решение подобного типа задач. + и –
Нет необходимости в дополнительных построениях каких-либо сечений, линейных углов, линий пересечения плоскостей. Полностью отсутствует доказательства, обоснование того или иного применения теорем стереометрии. +
Экономит время и место в оформлении задачи. +
Легко усваиваемый большинством учащихся с разной математической подготовкой. +
При решении не нужна высокая степень сообразительности, что негативно сказывается на творческих способностях учащихся. -
Одна и та же задача получает различное аналитическое представление в зависимости от того или иного выбора системы координат. -
Нацелен на результат ЕГЭ, т.е. в рамках учебного времени, даёт возможность «натаскивания» учащихся на решение подобного типа задач. + и –
Нет необходимости в дополнительных построениях каких-либо сечений, линейных углов, линий пересечения плоскостей. Полностью отсутствует доказательства, обоснование того или иного применения теорем стереометрии. +
Экономит время и место в оформлении задачи. +
Легко усваиваемый большинством учащихся с разной математической подготовкой. +