- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Квадратные уравнения
Содержание
- 1. Квадратные уравнения
- 2. Немного истории История Неполные квадратные уравнения и
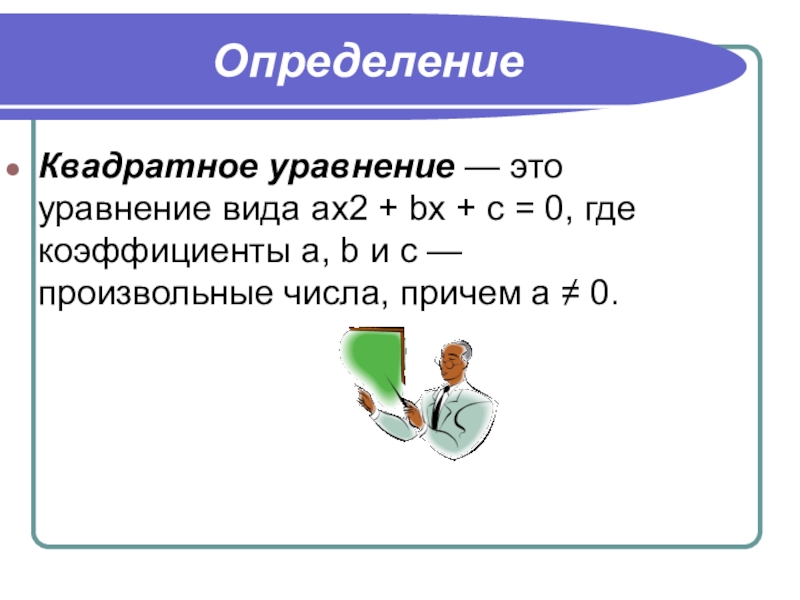
- 3. ОпределениеКвадратное уравнение — это уравнение вида ax2
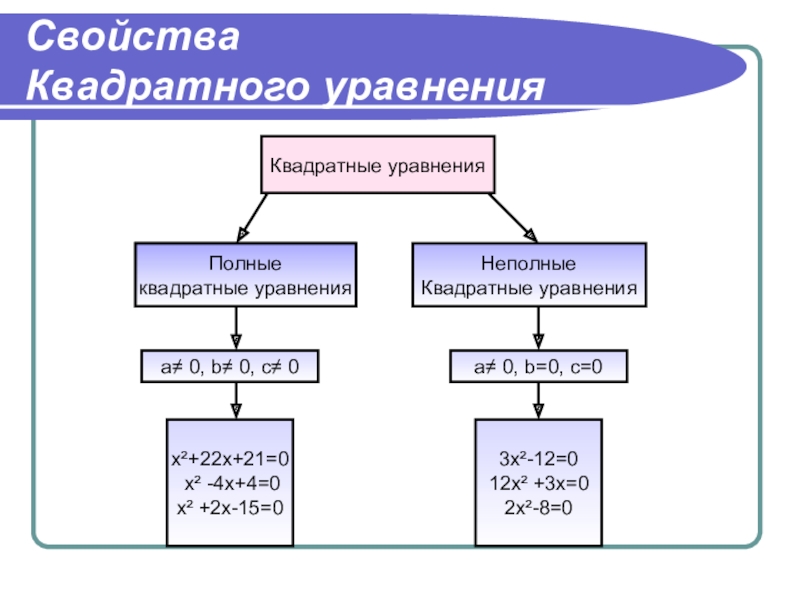
- 4. Свойства Квадратного уравненияКвадратные уравненияПолные квадратные уравненияНеполныеКвадратные
- 5. Определяем коэффициенты квадратных уравненийa) x²+22x+21=0a=1, b=22, c=21;б) 3x²-12=0a=3, b=0, c=1в) 2x²-4x+4x=0a=2, b=-4, c=4;
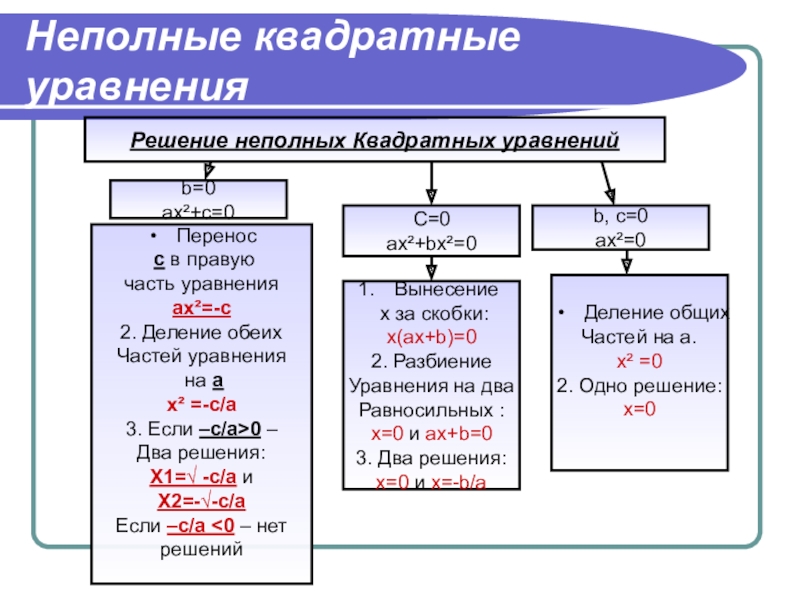
- 6. Неполные квадратные уравнения Решение неполных Квадратных уравнений
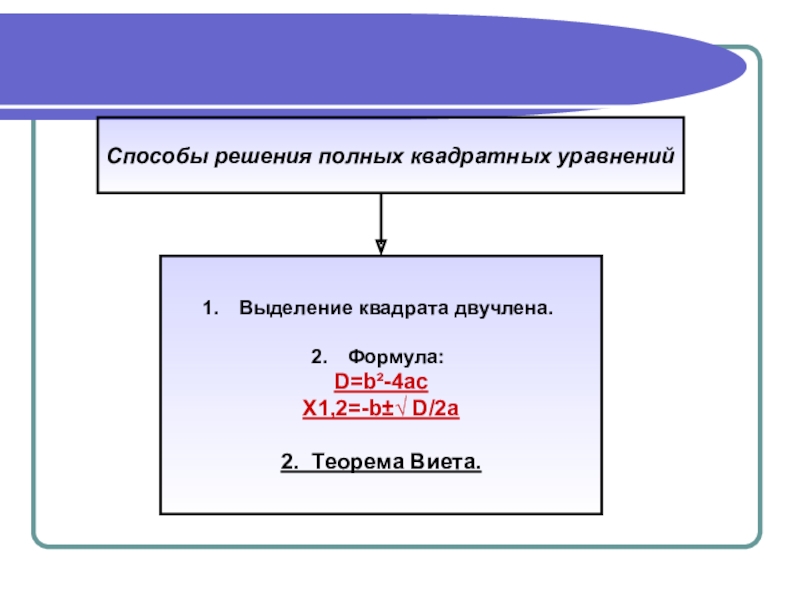
- 7. Способы решения полных квадратных уравненийВыделение квадрата двучлена. Формула:D=b²-4acX1,2=-b±√ D/2a2. Теорема Виета.
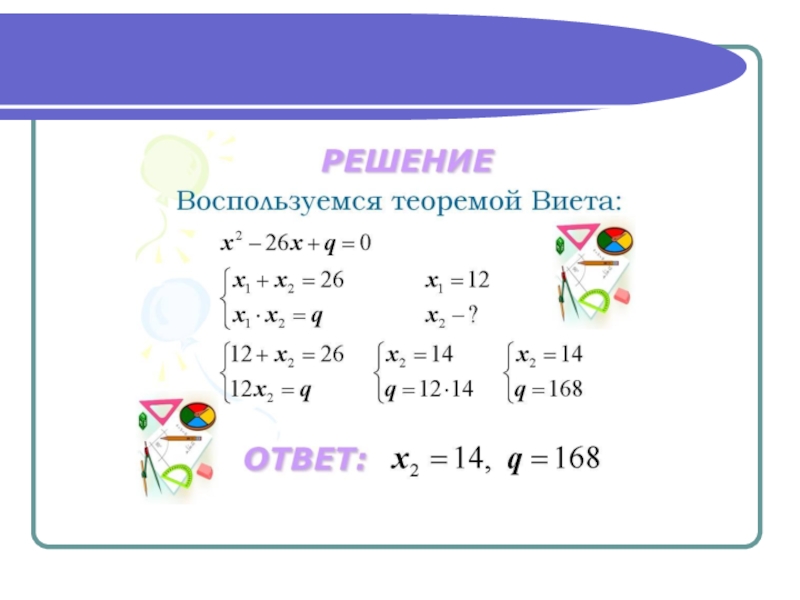
- 8. Теорема Виета Сумма корней приведенного квадратного трехчлена
- 9. Слайд 9
- 10. Спасибо за внимаениеШихвинцева Ольга 11 «А»
Немного истории История Неполные квадратные уравнения и частные виды полных квадратных уравнений умели решать вавилоняне. Об этом свидетельствуют найденные клинописные тексты задач с решениями(в виде рецептов).Приемы решения уравнений дает Диофант Александрийский .Правила решения квадратных уравнений дали
Слайд 2Немного истории
История Неполные квадратные уравнения и частные виды полных квадратных
уравнений умели решать вавилоняне. Об этом свидетельствуют найденные клинописные тексты задач с решениями(в виде рецептов).Приемы решения уравнений дает Диофант Александрийский .Правила решения квадратных уравнений дали индийский ученый Брахмагупта, хорезмский математик аль-Хорезми. немецкий математик М. Штифель, Нидерландский математик А. Жирар. После трудов Декарта, Ньютона, Виета способ решения квадратных уравнений принял современный вид.
Слайд 3Определение
Квадратное уравнение — это уравнение вида ax2 + bx + c
= 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Слайд 4Свойства
Квадратного уравнения
Квадратные уравнения
Полные
квадратные уравнения
Неполные
Квадратные уравнения
a≠ 0, b≠ 0, c≠
0
a≠ 0, b=0, c=0
x²+22x+21=0
x² -4x+4=0
x² +2x-15=0
3x²-12=0
12x² +3x=0
2x²-8=0
Слайд 5Определяем
коэффициенты квадратных уравнений
a) x²+22x+21=0
a=1, b=22, c=21;
б) 3x²-12=0
a=3, b=0, c=1
в) 2x²-4x+4x=0
a=2,
b=-4, c=4;
Слайд 6Неполные квадратные уравнения
Решение неполных Квадратных уравнений
b=0
ax²+c=0
C=0
ax²+bx²=0
b, c=0
ax²=0
Перенос
с в
правую
часть уравнения
аx²=-с
2. Деление обеих
Частей уравнения
на а
x² =-с/а
3. Если –с/а>0 –
Два решения:
Х1=√ -с/а и
Х2=-√-с/а
Если –с/a <0 – нет
решений
часть уравнения
аx²=-с
2. Деление обеих
Частей уравнения
на а
x² =-с/а
3. Если –с/а>0 –
Два решения:
Х1=√ -с/а и
Х2=-√-с/а
Если –с/a <0 – нет
решений
Вынесение
х за скобки:
x(ах+b)=0
2. Разбиение
Уравнения на два
Равносильных :
x=0 и ax+b=0
3. Два решения:
x=0 и x=-b/а
Деление общих
Частей на а.
x² =0
2. Одно решение:
x=0
Слайд 7Способы решения полных квадратных уравнений
Выделение квадрата двучлена.
Формула:
D=b²-4ac
X1,2=-b±√ D/2a
2. Теорема Виета.
Слайд 8Теорема Виета
Сумма корней приведенного квадратного трехчлена равна его второму коэффициенту
с противоположным знаком, а произведение - свободному члену .
Приведенное квадратное уравнение
По теореме Виета: