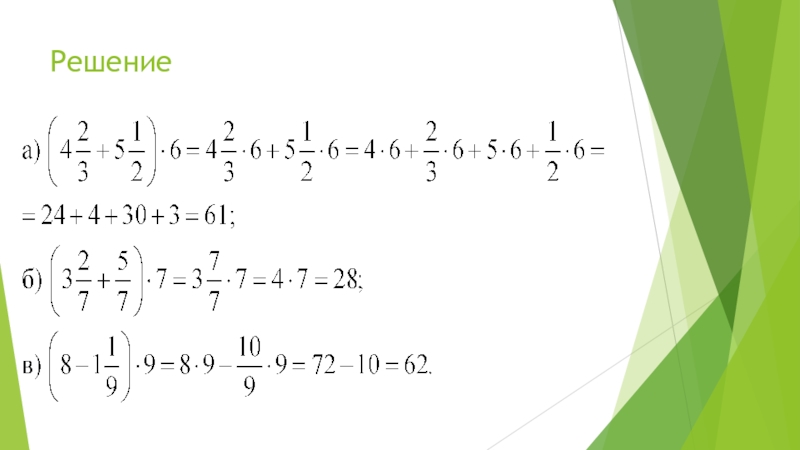- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Конспект+презентация на тему: Распределительное свойство умножения (6 класс, УМК Виленкин и др.)
Содержание
- 1. Конспект+презентация на тему: Распределительное свойство умножения (6 класс, УМК Виленкин и др.)
- 2. Математика - это язык, на котором написана книга природы. (Г. Галилей)
- 3. Распределительное свойство умножения относительно сложенияа · (в
- 4. Слайд 4
- 5. Правило умножения смешанного числа на натуральное числоЧтобы
- 6. Слайд 6
- 7. Решение
- 8. Задачи
- 9. Итог урокаУстно. Выполнить действия наиболее удобным способом:
- 10. Выберите фразеологизм,который характеризуют вашу работу сегодня
- 11. Домашнее заданиевыучить правило; решить № 567 (а; б; г), № 568 (а; б), № 573.
Математика - это язык, на котором написана книга природы. (Г. Галилей)
Слайд 3Распределительное свойство умножения относительно сложения
а · (в + с) = ав
+ ас
Распределительное свойство умножения относительно вычитания
а · (в – с) = ав – ас.
Слайд 5Правило умножения смешанного числа на натуральное число
Чтобы умножить смешанную дробь на
натуральное число, можно:
1) умножить целую часть на натуральное число;
2) умножить дробную часть на это натуральное число;
3) Сложить полученные результаты.
1) умножить целую часть на натуральное число;
2) умножить дробную часть на это натуральное число;
3) Сложить полученные результаты.
Слайд 10Выберите фразеологизм,который характеризуют вашу работу сегодня Шевелить мозгами; Краем уха;
Хлопать ушами.