- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Комбинаторная задача о числе точек пересечения прямых
Содержание
- 1. Комбинаторная задача о числе точек пересечения прямых
- 2. Известная комбинаторная задача1) Виленкин Н.Я., Виленкин А.Н.,
- 3. Задача о количестве точек пересечения n прямыхНа
- 4. Цели работы 1) обобщить одну из
- 5. Задача 1. Наличие параллельных прямых На плоскости
- 6. О методе рекуррентных соотношений Метод сведения комбинаторной задачи
- 7. Решение задачи №11) Наглядное нахождение закономерностей2) Нахождение
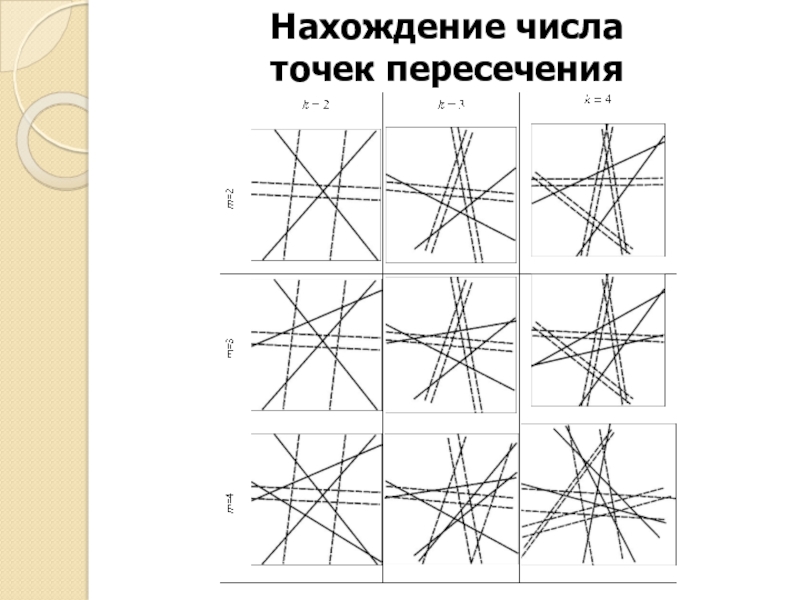
- 8. Нахождение числа точек пересечения
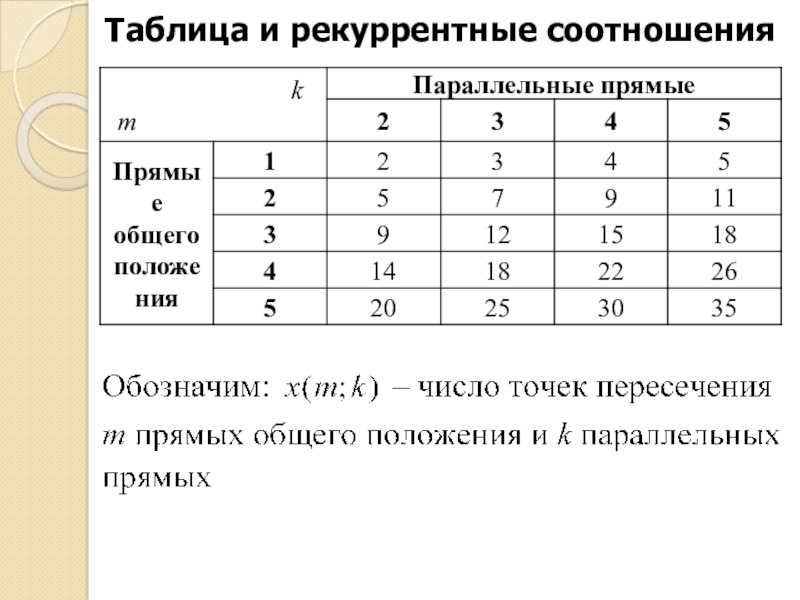
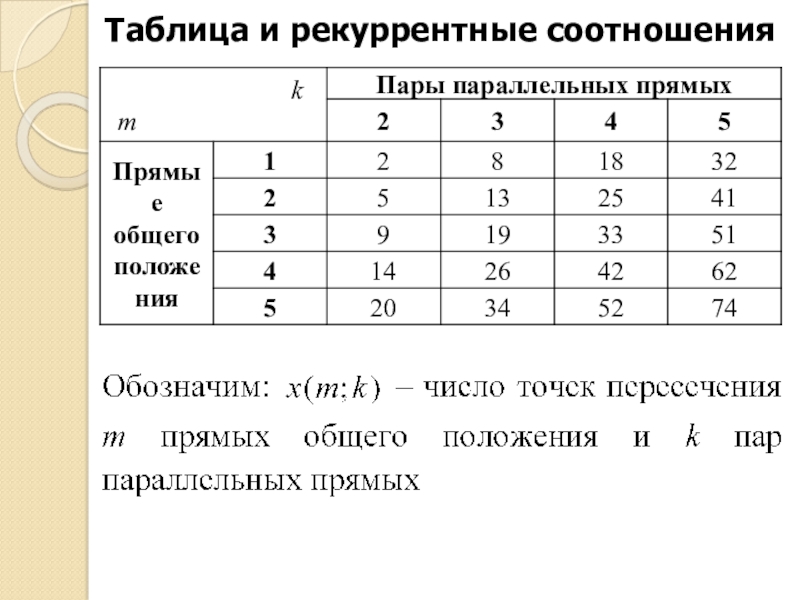
- 9. Таблица и рекуррентные соотношения
- 10. Рекуррентные соотношения
- 11. Нахождение формулы
- 12. Задача 2. Наличие пар параллельных прямыхНа плоскости
- 13. Решение задачи №21) Наглядное нахождение закономерностей2) Нахождение
- 14. Нахождение числа точек пересечения
- 15. Таблица и рекуррентные соотношения
- 16. Рекуррентные соотношения
- 17. Нахождение формулы
- 18. Выводы
- 19. Выводы
- 20. СПАСИБО ЗА ВНИМАНИЕ!
Известная комбинаторная задача1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.: МЦНМО, 2006.2) Смирнова И.М., Смирнов В.А. Комбинаторные задачи по геометрии (Библиотечка "Первого сентября". Математика. Вып. 5 (11)).– М.: Чистые пруды, 2006.
Слайд 2Известная комбинаторная задача
1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика.
–
М.: МЦНМО, 2006.
2) Смирнова И.М., Смирнов В.А. Комбинаторные задачи по геометрии (Библиотечка "Первого сентября". Математика. Вып. 5 (11)).
– М.: Чистые пруды, 2006.
2) Смирнова И.М., Смирнов В.А. Комбинаторные задачи по геометрии (Библиотечка "Первого сентября". Математика. Вып. 5 (11)).
– М.: Чистые пруды, 2006.
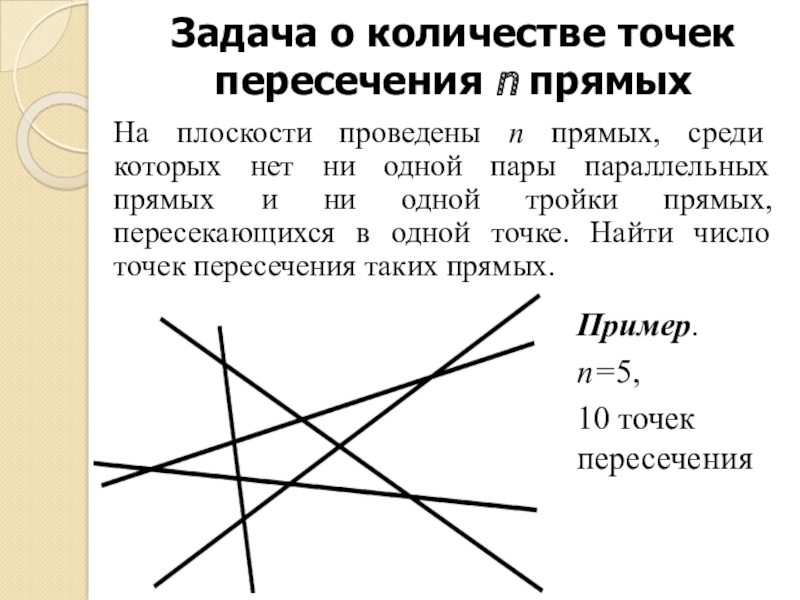
Слайд 3Задача о количестве точек пересечения n прямых
На плоскости проведены n прямых,
среди которых нет ни одной пары параллельных прямых и ни одной тройки прямых, пересекающихся в одной точке. Найти число точек пересечения таких прямых.
Пример.
n=5,
10 точек пересечения
Слайд 4 Цели работы
1) обобщить одну из известных комбинаторных задач по
геометрии и получить полное решение новых задач;
2) показать возможность применения метода рекуррентных соотношений для решения комбинаторных задач по геометрии.
2) показать возможность применения метода рекуррентных соотношений для решения комбинаторных задач по геометрии.
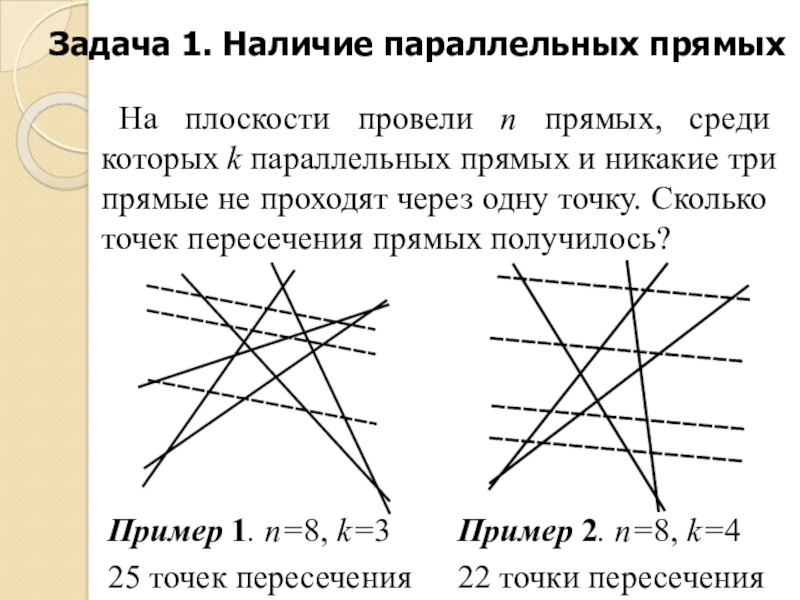
Слайд 5Задача 1. Наличие параллельных прямых
На плоскости провели n прямых, среди
которых k параллельных прямых и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось?
Пример 1. n=8, k=3
25 точек пересечения
Пример 2. n=8, k=4
22 точки пересечения
Слайд 6О методе рекуррентных соотношений
Метод сведения комбинаторной задачи к аналогичной задаче для
меньшего числа предметов с помощью некоторого соотношения называется методом рекуррентных соотношений.
Пользуясь рекуррентным соотношением, задачу с n предметами можно свести к задаче с n–1 предметом, потом к задаче с n–2 предметами и т.д.
Во многих случаях из рекуррентного соотношения удается получить явную формулу для решения комбинаторной задачи.
Пользуясь рекуррентным соотношением, задачу с n предметами можно свести к задаче с n–1 предметом, потом к задаче с n–2 предметами и т.д.
Во многих случаях из рекуррентного соотношения удается получить явную формулу для решения комбинаторной задачи.
Слайд 7Решение задачи №1
1) Наглядное нахождение закономерностей
2) Нахождение формулы, позволяющей найти количество
точек пересечения по любым значениям n и k
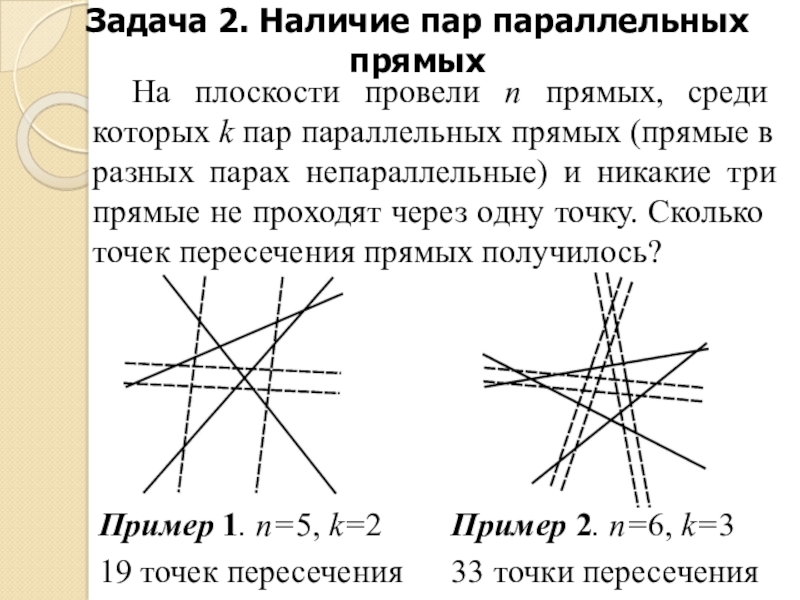
Слайд 12Задача 2. Наличие пар параллельных прямых
На плоскости провели n прямых, среди
которых k пар параллельных прямых (прямые в разных парах непараллельные) и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось?
Пример 1. n=5, k=2
19 точек пересечения
Пример 2. n=6, k=3
33 точки пересечения
Слайд 13Решение задачи №2
1) Наглядное нахождение закономерностей
2) Нахождение формулы, позволяющей найти количество
точек пересечения по любым значениям n и k