- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Интерактивная лекция Элементы статистики
Содержание
- 1. Интерактивная лекция Элементы статистики
- 2. Статистика ( от лат. status, состояние положение
- 3. Цель математической статистики создание методов сбора и
- 4. Задачи математической статистики указание методов сбора и
- 5. Случайная величина.Ее числовые характеристики
- 6. Величину называют случайной, если в результате испытания
- 7. Случайная величина, принимающая отдельные возможные значения с
- 8. Соответствие между отдельными возможными значениями и их вероятностями называется законом распределения дискретной случайной величины.
- 9. Дискретный вариационный ряд –ранжированная совокупность вариант с
- 10. Пример 1. В денежной лотерее на 100
- 11. Пример 2. Партия из 8 изделий содержит
- 12. Числовые характеристики СВПусть случайная величина Х может
- 13. Пример 5. Найти математическое ожидание количества очков,
- 14. Свойство 4. Математическое ожидание произведения независимых случайных
- 15. Дисперсия дискретной СВРазность между СВ и ее
- 16. Свойства дисперсииСвойство 1. Дисперсия постоянной величины С
- 17. Найдите дисперсию для примера 6.
- 18. Среднее квадратическое отклонениеСредним квадратическим отклонением случайной величины
- 19. Пример 8. Законы распределения независимых случайных величин
- 20. Решение. Согласно свойствам 2 и 3 дисперсии Законы распределения случайных величин Х2 и Y2:
- 21. Некоторые распределения случайных величин
- 22. Биномиальное распределениеПусть производится п независимых испытаний и
- 23. Пример 4. Банк выдает 5 кредитов. Вероятность
- 24. Закон распределения числа m наступлений события А
- 25. Распределение ПуассонаПусть в каждом из п производимых
- 26. Случайная величина принимает бесконечное, но счетное множество значений с постоянной вероятностью.M(X) = D(X) = Распределение Пуассона
- 27. Пусть в каждом из п производимых испытаний
- 28. Двумерные случайные величиныЗадаются прямоугольными или квадратными таблицами,
- 29. Двумерные случайные величиныСоставьте законы распределения случайных величин X,Y. Определите их числовые характеристики.
- 30. Описание связи между СВЦентральный момент порядка 1,
- 31. Корреляция показывает силу связи между двумя СВЕсли
- 32. Двумерные случайные величиныСоставьте законы распределения случайных величин X,Y. Определите их числовые характеристики. Установить зависимость
- 33. Решите задачи1. Партия из 8 изделий содержит
- 34. Решите задачи2. Ежедневные расходы на обслуживание и
- 35. Найдите дисперсию ежедневной продажи числа автомашинНайдите закон распределения отклонения числа проданных за день автомашин
- 36. 3. В лотереи разыгрывается автомобиль стоимостью 5
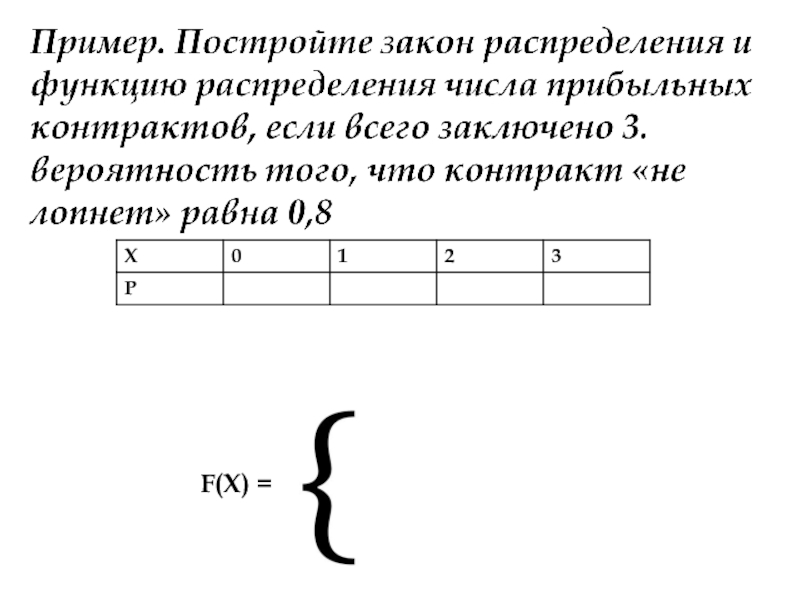
- 37. Функция распределенияФункцией распределения F(X) СВ Х называется
- 38. Свойства функции распределения
- 39. F(X) =
- 40. Элементы статистики
- 41. Понятие выборки. Статистические характеристикиГенеральная совокупность –совокупность всех
- 42. Основные понятияВыборка – данные, которые необходимо исследоватьГенеральная
- 43. Пример. Пусть из 2000 изделий отобрано для
- 44. Способы осуществления выборочной совокупности(выборки) после исследования объект
- 45. Выборка репрезентативная (представительная), если по ее данным
- 46. Независимые выборкиВыборки называются независимыми (несвязными), если процедура
- 47. Зависимые выборкиВыборки называются зависимыми (связными), если процедура
- 48. Статистические характеристикиОбъем выборкиРазмах выборкиСреднее арифметическоеМода Медиана Частота Относительная частота
- 49. Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
- 50. При изучении учебной нагрузки учащихся выделили группу
- 51. Имея этот ряд данных, можно определить, сколько
- 52. №1 Найдите среднее арифметическое чисел:А) 24,22,27,20,16,31
- 53. №2 В таблице приведены данные о продаже
- 54. №3 В аттестате о среднем образовании у
- 55. Размахом ряда чисел называется разность между наибольшим
- 56. №1 Каждый из 24 участников соревнования по
- 57. №2 На соревнованиях по фигурному катанию судьи
- 58. №3 Найдите размах ряда чисел.А) 32, 26,
- 59. Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
- 60. Правила нахождения модыЕсли все значения в выборке
- 61. Правила нахождения моды:3. Если два несмежных значения
- 62. Ряд чисел может иметь более одной моды
- 63. Пример. Пусть, проведя учет деталей, изготовленных за
- 64. №1 Найдите моду ряда чисел.45, 48, 85,
- 65. №2 В таблице записаны результаты ежедневного измерения
- 66. №3 В таблице показано число деталей, изготовленных
- 67. Медианой упорядоченного ряда чисел с нечетным числом
- 68. Правили нахождения медианыУпорядочить выборку по величинам входящих
- 69. Пример. В таблице показан расход
- 70. Пусть при сборе данных о расходе электроэнергии
- 71. №3 Ниже указана среднесуточная переработка сахара (в
- 72. Задача. В организации вели ежедневный учет поступивших
- 73. Относительная частота – отношение частоты к общему числу данных в ряду
- 74. 39, 43, 40, 0, 56, 38, 24,
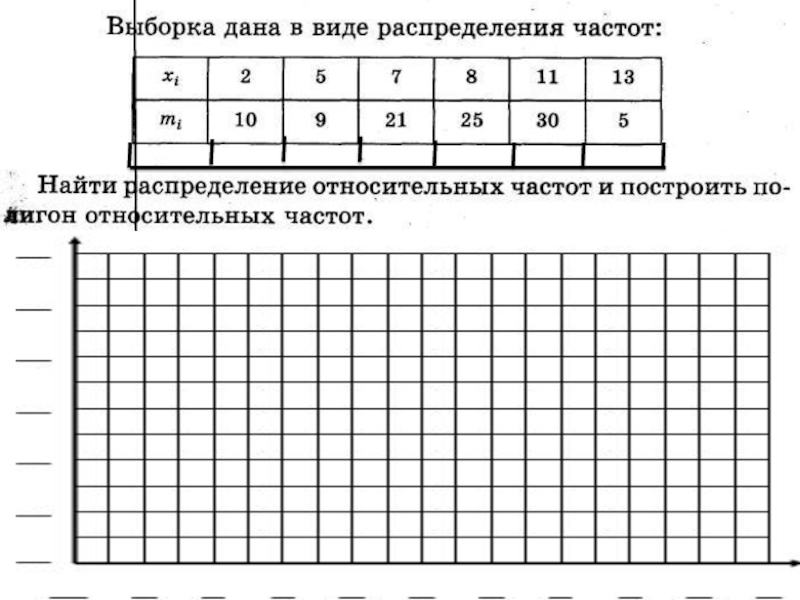
- 75. Пример 2.
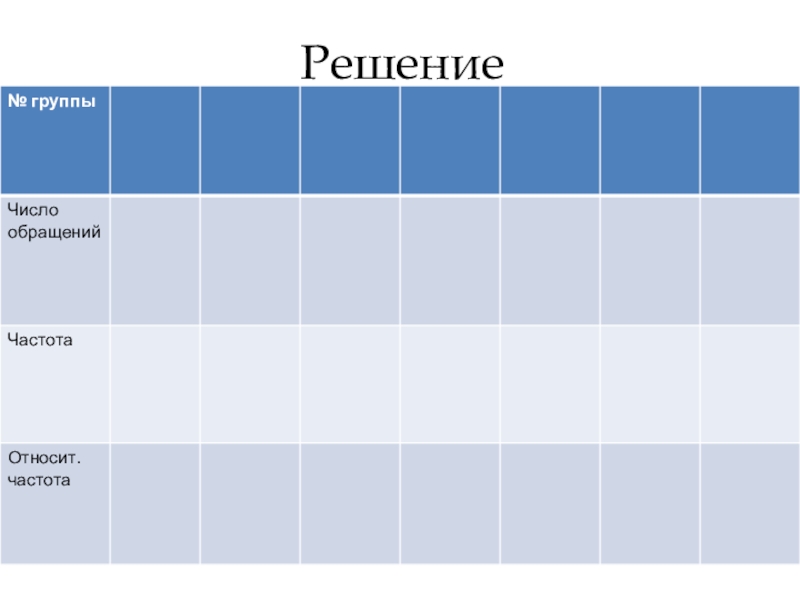
- 76. Решение
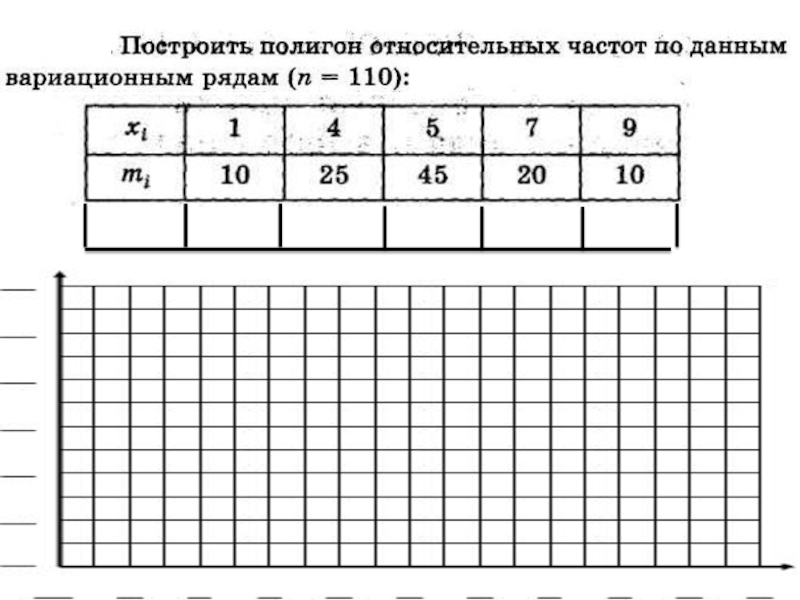
- 77. Пример 3
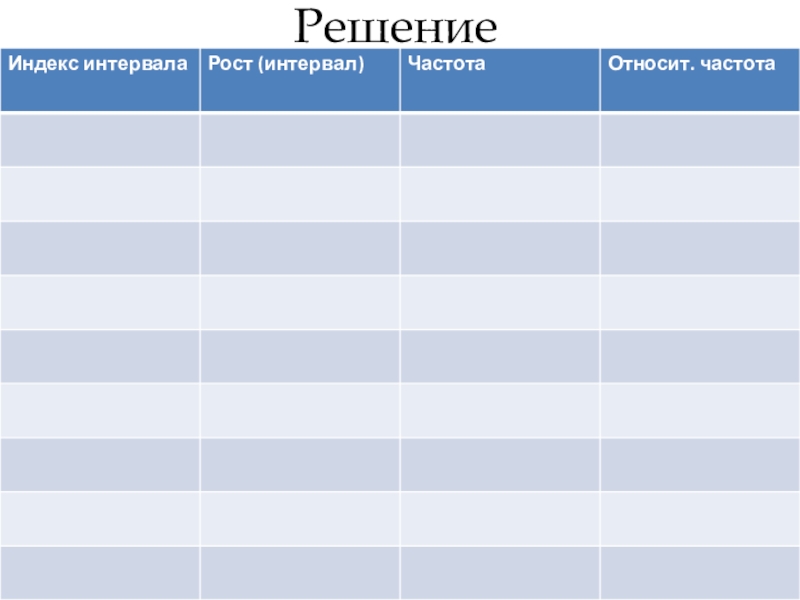
- 78. Решение
- 79. Слайд 79
- 80. Слайд 80
- 81. Слайд 81
- 82. Слайд 82
- 83. Слайд 83
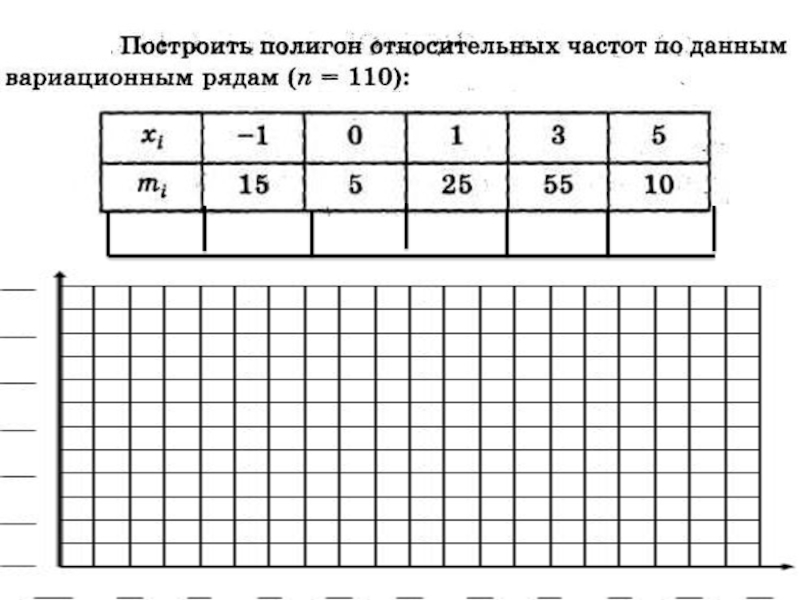
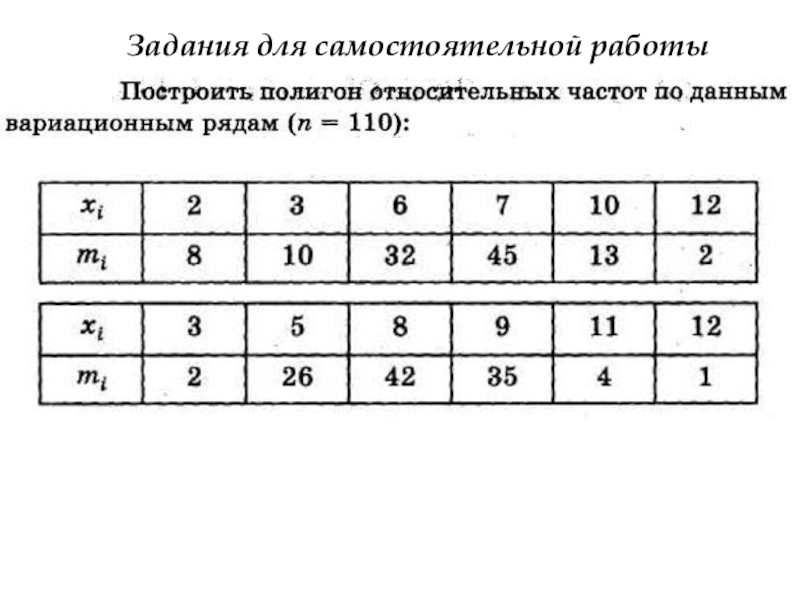
- 84. Задания для самостоятельной работы
- 85. Слайд 85
- 86. Слайд 86
- 87. Слайд 87
- 88. Слайд 88
- 89. Слайд 89
- 90. Слайд 90
Слайд 2Статистика
( от лат. status, состояние положение вещей)
- наука, которая
Слайд 3Цель математической статистики
создание методов сбора и обработки статистических данных для
Слайд 4Задачи математической статистики
указание методов сбора и группировки статистических сведений, которые
разработка методов анализа статистических данных
Слайд 6Величину называют случайной, если в результате испытания она примет лишь одно
Каждой случайной величине (СВ) соответствует множество чисел — это множество значений, которые она может принимать.
Например, число мальчиков среди 100 новорожденных
Обозначаются случайные величины прописными буквами, а их возможные значения — строчными буквами.
Например, случайная величина Х имеет два возможных значения x1 и х2.
Слайд 7Случайная величина, принимающая отдельные возможные значения с определенными вероятностями, называется дискретной
Непрерывной называется случайная величина, которая может принимать все значения из некоторого промежутка.
Слайд 8Соответствие между отдельными возможными значениями и их вероятностями называется законом распределения
Слайд 9Дискретный вариационный ряд –
ранжированная совокупность вариант с соответствующими им частотами.
Интервальный
упорядоченная последовательность интервалов изменения случайной величины с соответствующими частотами попадания в каждый из них.
Слайд 10Пример 1. В денежной лотерее на 100 билетов разыгрывается один выигрыш
Слайд 11
Пример 2. Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются
Случайная величина Х — число стандартных деталей среди отобранных — может принимать 4 возможных значения: 0, 1, 2 и 3.
Вероятность нахождения k стандартных изделий среди трех отобранных определяется формулой
Слайд 12Числовые характеристики СВ
Пусть случайная величина Х может принимать значения x1, x2,
Математическим ожиданием дискретной СВ называется сумма произведений всех ее возможных значений на их вероятности:
Слайд 13Пример 5. Найти математическое ожидание количества очков, выпадающих при бросании игральной
Свойства математического ожидания
Свойство 1. Математическое ожидание постоянной величины С равно этой постоянной:
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
Свойство 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:
Слайд 14Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их
Пример 6. Пусть ежедневные расходы на обслуживание и рекламу автомобилей в некотором автосалоне составляют в среднем 100 тыс. р., а число продаж Х автомашин в течение дня подчиняется следующему закону распределения:
Найти математическое ожидание ежедневной прибыли при цене на машину 150 тыс. р.
Решение. Ежедневная прибыль подсчитывается по формуле
Слайд 15Дисперсия дискретной СВ
Разность между СВ и ее математическим ожиданием называется отклонением.
Математическое
или
Слайд 16Свойства дисперсии
Свойство 1. Дисперсия постоянной величины С
равна нулю:
Свойство 2. Постоянный
Свойство 3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий:
Слайд 18Среднее квадратическое отклонение
Средним квадратическим отклонением случайной величины Х (стандартом) называется квадратный
Пример 7. Найти дисперсию и среднее квадратическое отклонение случайной величины X, заданной следующим распределением:
Слайд 19Пример 8. Законы распределения независимых случайных величин Х и Y приведены
Найти дисперсию и среднее квадратическое отклонение случайной величины Z = 2Х + 3Y.
Слайд 20Решение. Согласно свойствам 2 и 3 дисперсии
Законы распределения случайных величин
Слайд 22Биномиальное распределение
Пусть производится п независимых испытаний и в каждом из них
Этот закон получил название биноминального распределения потому, что правая часть равенства представляет собой общий член разложения бинома Ньютона
Слайд 23Пример 4. Банк выдает 5 кредитов. Вероятность невозврата кредита равна 0,2
Обозначим р = 0,2, q = 0,8
Слайд 24Закон распределения числа m наступлений события А в n независимых испытаниях,
M(X) = np
D(X) = npq
Биномиальное распределение
Слайд 25Распределение Пуассона
Пусть в каждом из п производимых испытаний вероятность появления события
Для случая малых значений р и больших значений п используется формула Пуассона
Произведение пр - постоянная величина,
т.е. пр = λ.
Вероятность того, что событие А наступит ровно k раз
Слайд 26Случайная величина принимает бесконечное, но счетное множество значений с постоянной вероятностью.
M(X)
Распределение Пуассона
Слайд 27Пусть в каждом из п производимых испытаний вероятность появления события А
При больших п пользуются формулой Лапласа
Распределение Лапласа
Вероятность того, что событие А появится в п испытаниях ровно k раз, приближенно равна значению функции φ(x):
Слайд 28Двумерные случайные величины
Задаются прямоугольными или квадратными таблицами, в которых отражены значения
Слайд 29Двумерные случайные величины
Составьте законы распределения случайных величин X,Y. Определите их числовые
Слайд 30Описание связи между СВ
Центральный момент порядка 1, называемый ковариацией случайных величин
= cov (X, Y) = M(XY) – M(X)M(Y)
Ковариация показывает наличие положительной или отрицательной связи, но не позволяет определить силу зависимости.
Слайд 31Корреляция показывает силу связи между двумя СВ
Если =
Описание связи между СВ
Слайд 32Двумерные случайные величины
Составьте законы распределения случайных величин X,Y. Определите их числовые
Слайд 33Решите задачи
1. Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются
Слайд 34Решите задачи
2. Ежедневные расходы на обслуживание и рекламу автомобилей в салоне
Найдите математическое ожидание ежедневной прибыли при цене на машину 150 000 руб.
Слайд 35Найдите дисперсию ежедневной продажи числа автомашин
Найдите закон распределения отклонения числа проданных
Слайд 363. В лотереи разыгрывается автомобиль стоимостью 5 000 ден. ед., 5
Слайд 37Функция распределения
Функцией распределения F(X) СВ Х называется вероятность того, что величина
F(x) = P(X
Слайд 41Понятие выборки.
Статистические характеристики
Генеральная совокупность –совокупность всех исследуемых объектов.
Выборка – любая подгруппа
Слайд 42Основные понятия
Выборка – данные, которые необходимо исследовать
Генеральная совокупность – совокупность объектов,
Выборочная совокупность – совокупность случайно отобранных объектов из генеральной совокупности.
Число объектов в совокупности называется ее объемом.
Слайд 43Пример.
Пусть из 2000 изделий отобрано для обследования 100 изделий. Тогда
Слайд 44Способы
осуществления выборочной совокупности
(выборки)
после исследования объект из выборки возвращается в
после исследования объект из выборки не возвращается в генеральную совокупность, то выборка называется бесповторной (безвозвратной).
Слайд 45Выборка репрезентативная
(представительная),
если по ее данным можно достаточно уверенно судить
Слайд 46Независимые выборки
Выборки называются независимыми (несвязными), если процедура эксперимента и полученные результаты
Слайд 47Зависимые выборки
Выборки называются зависимыми (связными), если процедура эксперимента и полученные результаты
Слайд 48Статистические характеристики
Объем выборки
Размах выборки
Среднее арифметическое
Мода
Медиана
Частота
Относительная частота
Слайд 49Средним арифметическим ряда чисел
называется частное от деления суммы этих чисел
Слайд 50При изучении учебной нагрузки учащихся выделили группу из 12 семиклассников. Их
23,18,25,20,25,25,32,37,34,26,34,25.
Слайд 51Имея этот ряд данных, можно определить, сколько минут в среднем затратили
=
Число 27, полученное в результате, называют
средним арифметическим рассматриваемого
ряда чисел.
= 27
Слайд 52№1 Найдите среднее арифметическое чисел:
А) 24,22,27,20,16,31
Б) 11,9,7,6,2,0,1 Г) 144,146,114,138.
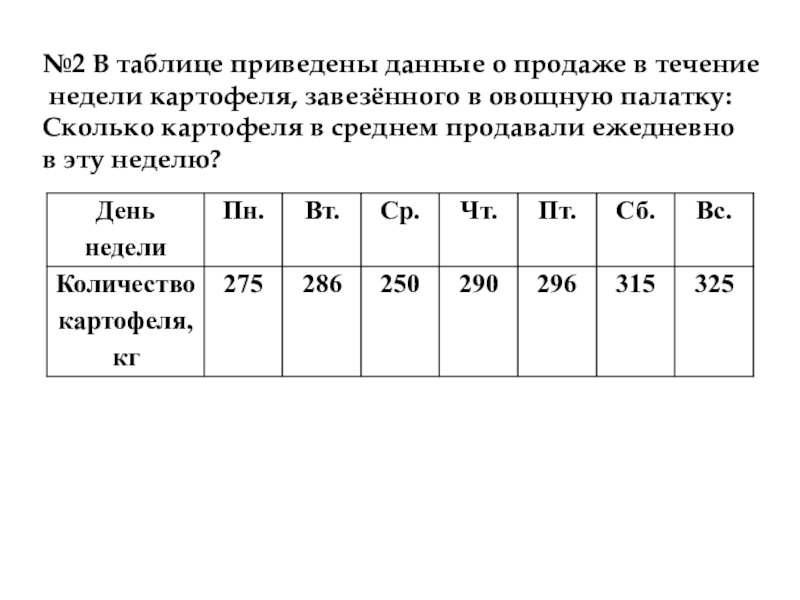
Слайд 53№2 В таблице приведены данные о продаже в течение
недели картофеля,
Сколько картофеля в среднем продавали ежедневно
в эту неделю?
Слайд 54№3 В аттестате о среднем образовании у четверых друзей- выпускников школы-
Ильин: 4,4,5,5,4,4,4,5,5,5,4,4,5,4,4
Романов: 3,3,4,4,4,4,43,4,4,4,5,3,4,4
Семёнов: 3,4,3,3,3,3,4,3,3,3,3,4,4,5,4
Попов: 5,5,5,5,5,4,4,5,5,5,5,5,4,4,4.
С каким средним балом окончил школу каждый из этих выпускников?
Слайд 55Размахом ряда чисел
называется разность
между наибольшим и наименьшим
из этих
Размах ряда находят тогда, когда хотят определить, как велик разброс данных в ряду.
Слайд 56
№1 Каждый из 24 участников соревнования по стрельбе произвел по десять
6,5,5,6,8,3,7,6,8,5,4,9, 7,7,9,8,6,6,5,6,4,3,6,5.
Найдите для этого ряда размах.
Слайд 57№2 На соревнованиях по фигурному катанию судьи поставили спортсмену следующие оценки:
5,2; 5,4; 5,5; 5,4; 5,1; 5,1; 5,4; 5,5; 5,3.
Для полученного ряда чисел найдите размах. Каков смысл этого показателя?
Слайд 58№3 Найдите размах ряда чисел.
А) 32, 26, 18, 26, 15, 21,
Б) 67,1, 68,2, 67,1, 70,4, 68,2;
В) 21, 18,5, 25,3, 18,5, 17,9;
Г) 0,6, 0,8, 0,5, 0,9, 1,1.
Слайд 60Правила нахождения моды
Если все значения в выборке встречаются одинаково часто, то
Если два соседних значения имеют одинаковую частоту и их частоты больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений.
Слайд 61Правила нахождения моды:
3. Если два несмежных значения имеют равные частоты, большие
4. Если мода оценивается по множеству сгруппированных данных, то для нахождения моды определяют группу с наибольшей частотой признака.
Слайд 62Ряд чисел может иметь более одной моды
или не иметь её
47, 46, 50, 52, 47, 52, 49, 45, 43, 53- (имеет)
69, 68, 66, 70, 67, 71, 74, 63, 73, 72- (не имеет)
Слайд 63Пример. Пусть, проведя учет деталей, изготовленных за смену рабочими одной бригады,
36, 35, 35,36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38 ,38, 39 ,39, 36.
Найдите для него моду ряда чисел.
Для этого удобно предварительно составить из полученных данных упорядоченный ряд чисел, т.е.такой ряд, в котором каждое последующее число меньше (или больше) предыдущего. Получили:
35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 38, 38, 38, 39, 39, 39 ,39.
Ответ. Число 36 является модой этого ряда чисел.
Слайд 64№1 Найдите моду ряда чисел.
45, 48, 85, 31, 23, 45, 67,
Слайд 65№2 В таблице записаны результаты ежедневного измерения на метеостанции в полдень
Найдите моду ряда чисел и сделайте вывод, в какие числа марта температура воздуха была одинаковой. Найдите среднюю температуру воздуха.
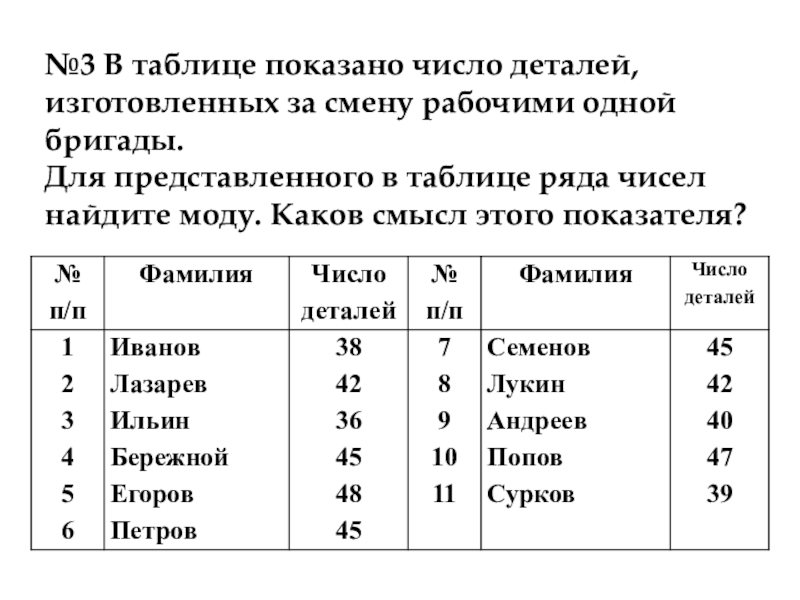
Слайд 66№3 В таблице показано число деталей, изготовленных за смену рабочими одной
Для представленного в таблице ряда чисел найдите моду. Каков смысл этого показателя?
Слайд 67Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное
Медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Слайд 68
Правили нахождения медианы
Упорядочить выборку по величинам входящих в нее значений.
2. Середина
3. Если «середины» две (т.е. число элементов четное) то медианой будет среднее арифметическое этих значений.
Слайд 69 Пример. В таблице показан расход электроэнергии в январе жильцами
Составим упорядоченный ряд:
64, 72, 72, 75, 78, 82, 85, 91, 93.
В полученном упорядоченном ряду девять чисел. Нетрудно заметить, что в середине ряда расположено число 78.
Число 78 является серединным числом, или медианой, рассматриваемого упорядоченного ряда чисел.
Слайд 70Пусть при сборе данных о расходе электроэнергии к указанным девяти квартирам
Представим полученные данные в виде упорядоченного ряда чисел:
64, 72, 72, 75, 78, 82, 85, 88, 91, 93.
В этом числовом ряду четное число членов и имеются два числа, расположенные в середине ряда: 78 и 82. Найдем среднее арифметическое этих чисел (78 + 82) : 2 = 80.
Медианой рассматриваемого упорядоченного ряда является число 80.
,
Слайд 71№3 Ниже указана среднесуточная переработка сахара (в тыс. ц) заводами сахарной
12,2, 13,2, 13,7, 18,0 18,6 12,2 18,5 12,4 14,2 17,8.
Для представленного ряда данных найдите медиану.
Слайд 72
Задача. В организации вели ежедневный учет поступивших в течение месяца писем.
39, 43, 40, 0, 56, 38, 24, 21, 35, 0, 58, 31, 49, 38, 25, 34, 0, 52, 40, 42, 40, 39, 54, 0, 64, 44, 50, 38, 37, 32.
Найдите статистические характеристики данного числового ряда
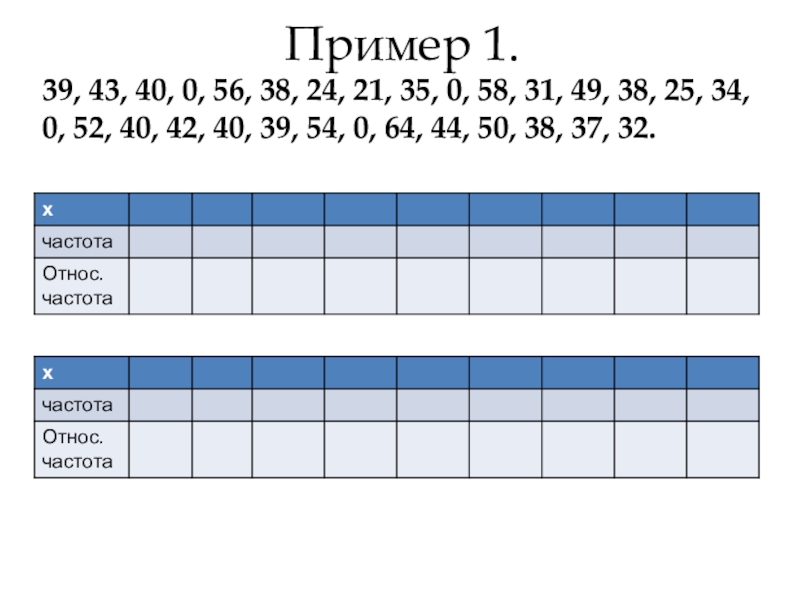
Слайд 7439, 43, 40, 0, 56, 38, 24, 21, 35, 0, 58,
Пример 1.