- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Эстетическая составляющая урока
Содержание
- 1. Эстетическая составляющая урока
- 2. «Математика владеет не только истиной, но и
- 3. Выбрав данную тему, я ставлю следующие цели
- 4. Математика (глазами обучающихся)
- 5. Математика(глазами учителя)точная
- 6. Очень важно, что учитель вкладывает в слова:
- 7. Мои принципы педагогической деятельности, обусловленные идеей нравственно-эстетического
- 8. История математики – благодатный материал для развития
- 9. Нередко, однако, о можно услышать высказывания о
- 10. Важной мерой красоты является порядок, который
- 11. Музыка и математика. Сегодня эти два слова
- 12. Математическая задача способствует формированию и развитию эстетического
- 13. Искусство устного счета на определенной ступени своего
- 14. Не перечислить всех достоинств оригами в развитии
- 15. Эстетический потенциал школьной математики в большой мере
- 16. Слайд 16
- 17. Примером самостоятельного открытия или еще каких-либо математических
- 18. В своей работе я привела лишь
Слайд 1Подготовил доклад: учитель математики
Барышникова Марина Александровна
Эстетическая составляющая
урока математики
Слайд 2«Математика владеет не только истиной, но и высшей красотой - красотой
«Знания вне чувства, лишь светят, а не греют, не способны перейти в действие». В. Г. Белинский
«Не волнуя, не затрагивая нервную систему, нельзя даже просто агитировать, нельзя, например, даже собирать толпу и пойти тушить пожар. Тем более нельзя без этого воспитывать. Поэтому эмоциональной окраской учебного материала, вызвав эмоциональные порывы, вызвав эмоциями видоизменения в сознании учеников, можно придать воспитательный характер любому процессу восприятия того или другого внешнего воздействия». А.В. Луначарский
«Красоту математики (её простоту, симметрию, сжатость и полноту) можно и следует дать почувствовать даже очень малым детям. Когда этот предмет излагают должным образом и притом конкретно, то усвоение математики сопровождается эмоциями и наслаждением красотой». Юнг
Слайд 3Выбрав данную тему, я ставлю следующие цели и задачи выполнения работы,
раскрыть достоинства эстетического развития учащихся как средства способствующего привитию интереса к предмету;
показать нетрадиционные подходы эстетического развития учащихся на уроках и во внеклассной работе, пути и методы реализации потенциала математики как части искусства;
раскрыть воспитательное воздействие математики в культурном развитии учащихся;
помочь учителям в разъяснении учащимся целесообразности и необходимости изучения математики как одной из составляющих эстетики.
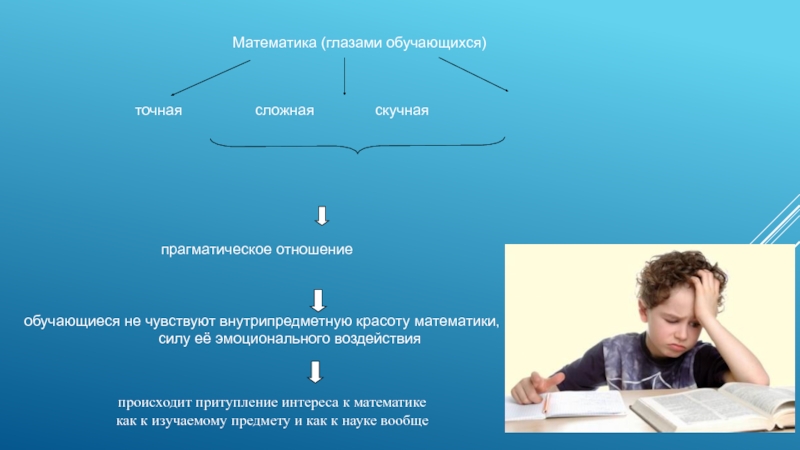
Слайд 4Математика (глазами обучающихся)
точная сложная скучная
при изучении нет
прагматическое отношение
(выучить, чтобы сдать экзамены, поступить в ВУЗ и т.д.)
обучающиеся не чувствуют внутрипредметную красоту математики,
силу её эмоционального воздействия
происходит притупление интереса к математике
как к изучаемому предмету и как к науке вообще
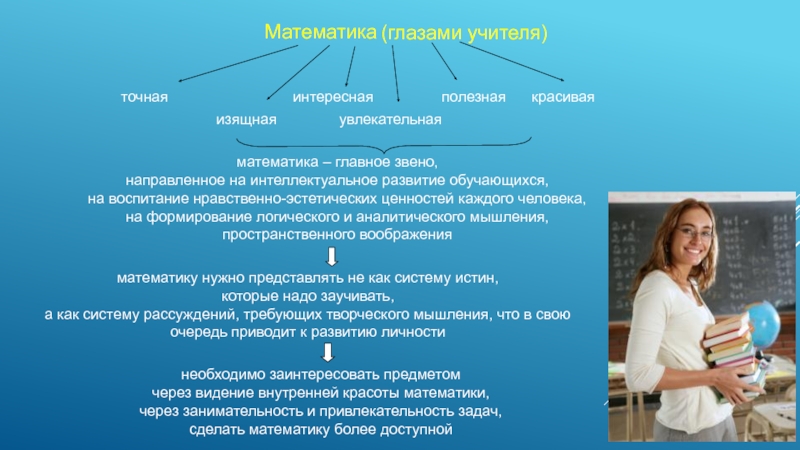
Слайд 5Математика
(глазами учителя)
точная
изящная увлекательная
математика – главное звено,
направленное на интеллектуальное развитие обучающихся,
на воспитание нравственно-эстетических ценностей каждого человека,
на формирование логического и аналитического мышления,
пространственного воображения
математику нужно представлять не как систему истин,
которые надо заучивать,
а как систему рассуждений, требующих творческого мышления, что в свою очередь приводит к развитию личности
необходимо заинтересовать предметом
через видение внутренней красоты математики,
через занимательность и привлекательность задач,
сделать математику более доступной
Слайд 6Очень важно, что учитель вкладывает в слова: "изложить материал", "преподать его".
В это время сами как бы раздваиваемся на знающего учителя и незнающего, непонимающего ученика. Тогда учитель с учеником вместе постигают проблему, «вживаясь» в мир друг друга: ребенок идет впереди, а преподаватель исподволь «открывает» ему глаза на «дорогу к вершине познаний». Получается, что ученик идет по ней самостоятельно, покоряя эту вершину сам.
Слайд 7Мои принципы педагогической деятельности, обусловленные идеей нравственно-эстетического воспитания обучающихся на уроках
системность обучения, предполагающая соблюдение взаимного соответствия целей, содержания, форм, методов, средств обучения и оценивания результатов; создание целостности математических знаний; видение математики через призму эстетики;
организация совместной работы учителя и обучающихся, предполагающая планирование, реализацию и оценивание процесса и результата обучения;
креативность обучения, предполагающая реализацию творческих возможностей учителя и ученика;
опора на имеющийся ценностный потенциал обучающихся;
развитие познавательных потребностей, предполагающее выявление наличия устойчивого интереса к изучению математики, что способствует осознанному усвоению математических знаний, умений, навыков, приводящее, в свою очередь, к высокому уровню освоения учебного материала;
гуманизация и гуманитаризация математического образования, предполагающие максимум внимания развитию личностных качеств каждого ученика, воспитанию нравственно-эстетических ценностей каждого человека;
демократизация отношений, учитывающая соблюдение принципа диалога "учитель – ученик", а также протекание процесса обучения в атмосфере сотрудничества, соуправления всех участников педагогического процесса;
природосообразность обучения и воспитания, обусловленная культурологическим подходом.
Слайд 8История математики – благодатный материал для развития эстетического вкуса школьников Математика
Старинная греческая задача. На вопрос: сколько учеников обучается у Пифагора в школе, он ответил, что половина всех его учеников изучает математику, четверть – музыку, седьмая часть – молчит и, кроме того, есть ещё три женщины. Сколько учеников у Пифагора?
Старинная китайская задача. Несколько человек покупают барана. Если каждый внесёт по 5 монет, то не хватит до стоимости 45 монет, если же каждый внесёт по 7 монет, то не хватит 3-х монет. Сколько стоит баран?
Индийский мыслитель Бхаскара (1114-1178), решая квадратное уравнение х2 – 45х =250 находит впервые два корня: 50 и -5 и делает замечание, что второе значение брать не следует «…ведь люди не воспринимают отрицательных, абстрактных чисел». Алгебраические задачи на составление квадратных уравнений индийские учёные записывали в стихотворной форме и рассматривали их как особый вид искусства.
Интерес вызывают сведения о роли природного инструмента человека, его пальцев и рук.
Слайд 9Нередко, однако, о можно услышать высказывания о том, что математика –
Слайд 10Важной мерой красоты является порядок, который
Поворотную симметрию мы видим в стройных елях и кипарисах, в волшебных узорах снежинок.
Переносную симметрию с удовольствием и радостью наблюдаем в ажурных оградах парков, решетках мостов и балконов.
Трансляционной симметрией любуемся, рассматривая рисунки на обоях, кружевах на воротниках и манжетах, на причудливом, играющем на солнце узоре на шкуре змеи.
Цветную симметрию наблюдаем в шахматных фигурах, расставленных в одинаковом порядке на шахматной доске. Симметрия воспринимается человеком как проявление закономерного порядка, царящего в природе.
«Порядок освобождает мысль», - любил повторять великий французский математик и философ Рене Декарт. Симметрия воспринимается человеком слишком статично, скованно, и только единство симметрии и асимметрии создаёт подлинную гармонию красоты.
Слайд 11Музыка и математика. Сегодня эти два слова редко стоят вместе. Между
На уроке можно рассмотреть более широкое представление понятия «функция» и выявим интересную зависимость между натуральными числами, цветами радуги и нотами в музыкальной гамме. Ребята, сколько всего нот в музыкальной гамме? Кто перечислит их? Сколько цветов радуги?
Эти семь нот лежат в основе любой музыки. Самая разная и при разных обстоятельствах звучит в нашей жизни музыка. Она звучит по радио, телевидению, в кино, в грамзаписи; музыка заполняет концертные и театральные залы; мы слышим музыку в детских садах и школах, на спортивных соревнованиях, в цирке и на дискотеке. Музыка, также как и литература, и живопись, и математика расширяет наше знакомство с окружающим миром.
Оказывается, можно установить зависимость между множеством всех натуральных чисел, цветами радуги и нотами.
Числу 1 соответствует нота «до», числу 2 – «ре» и далее по таблице.
Начиная с числа 8, все повторяется. А как определить ноту для числа 29?
Правильно, надо найти остаток от деления 29 на 7! Это будет 1.
Значит, числу 29 соответствует нота «до». А как определить ноту для числа 35?
Верно, число 35 делится нацело на 7, значит, ему соответствует нота «си».
1
2
Слайд 12Математическая задача способствует формированию и развитию эстетического вкуса учеников в том
условие задачи должно быть интересно школьнику, если задача геометрическая, она должна сопровождаться красивым рисунком;
задача должна обладать большой степенью общности;
задача может устанавливать интересный факт, порой неожиданный;
в решение задачи обязательно нужно спрятать "изюминку", чтобы оно было наглядно и удивительно просто;
желательно, чтобы было несколько способов решения задачи.
Формируя и развивая эстетический вкус при решении "красивых" задач, учитель помогает школьникам более полно воспринять красоту математики вообще, старается повысить их математическую и общую культуру.
Слайд 13Искусство устного счета на определенной ступени своего совершенства также становится эстетическим
Например, учащихся можно познакомить с индийской тайной быстрого умножения и показать ее красоту на простом примере. Умножим 94 на 98: дополнения до ста – соответственно 6 и 2; вычтем из первого множителя дополнение второго (94-2=92) или из второго множителя дополнение первого (98-6=92). И в том, и в другом случае получили 92; это первые цифры искомого произведения; перемножаем дополнения (6∙2 =12); 12 – это последние цифры произведения; итак, 94 ∙ 98= 9212.
Умножение двузначного числа на 11: 52 * 11 Сложим эти две цифры и вставим полученную сумму вместо пробела, как показано здесь: 5_(5+2)_2= 572
Если при сложении получается двузначное число, просто вставьте вместо пробела вторую цифру полученной суммы, а первую прибавьте к первой "отделенной" цифре, как показано здесь: 89 * 11=>8_(9+9)_9=>(8+1)_8_9=>9_8_9=989
Быстрый квадрат: Если Вам необходимо возвести в квадрат двузначное число заканчивающееся на 5 воспользуйтесь следующим трюком. Умножьте первую цифру числа на сумму этой цифры плюс 1, а к концу всего припишите 25: 252 = (2*(2+1)) дописать 25 2 * 3 = 6. Ответ: 625
Умножение на 9. Это очень просто, для умножения любого числа от 1 до 9 на 9 поверните раскрытые ладони перед своим лицом, загните палец соответствующий цифре на которую Вы хотите умножить 9 (к примеру 9 * 3, загните третий палец), посчитайте пальцы до и после загнутого пальца, это и будут десятки и единицы искомого числа, т.е. 2 и 7. Ответ: 27
Слайд 14Не перечислить всех достоинств оригами в развитии ребенка.
Доступность бумаги как
Оригами развивает у учащихся способность работать руками под контролем сознания, происходит развитие глазомера.
Оригами способствует концентрации внимания, так как заставляет сосредоточиться на процессе изготовления, чтобы получить желаемый результат.
Оригами имеет огромное значение в развитии конструктивного мышления детей, их творческого воображения, художественного вкуса, стимулирует развитие памяти, так как ребенок должен запомнить последовательность ее изготовления.
Оригами способствует четкому запоминанию таких геометрических понятий, как угол, сторона, квадрат, треугольник и т.д.
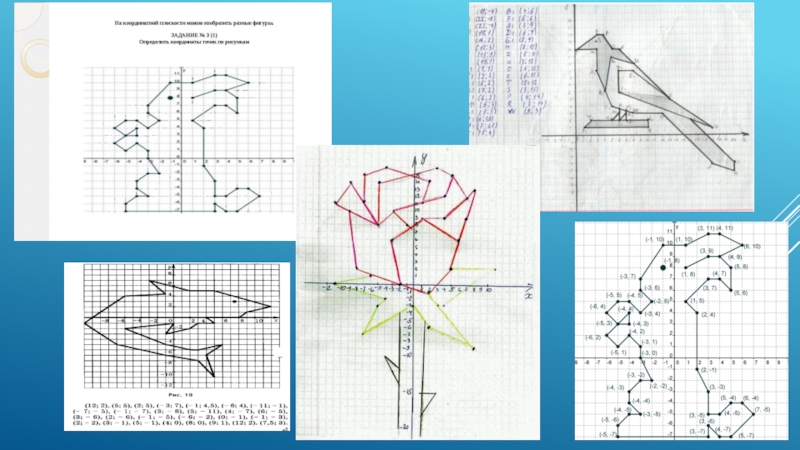
Слайд 15Эстетический потенциал школьной математики в большой мере проявляется в, так называемых,
В практике обучения математике "красивые" задания на координатной плоскости чаще всего формулируются так: "Построй точки по заданным координатам, соедини их отрезками подходящим образом, и ты получишь фигуру, изображающую …". Обучающимся можно предложить творческие задания на самостоятельное составление какой-либо красивой фигурки и определение координат её узловых точек.
Слайд 17Примером самостоятельного открытия или еще каких-либо математических фактов может служить урок
никто не заставляет детей работать, не указывает, а лишь сопровождает;
"свет в конце тоннеля" они увидели сами;
учитель предоставил им возможность самостоятельно совершить интеллектуальное путешествие, хотя был всегда рядом в качестве помощника;
к истине ребята подошли путем экспериментального "нащупывания".
Как следствие – интерес к предмету математики, развитие творческих способностей, взаимопонимание, взаимовоспитание, взаимопомощь.
Слайд 18 В своей работе я привела лишь некоторые примеры, подтверждающие многие
Очень важна и эмоциональная сторона подачи учебного материала. Искренне считаю, что жизнь настоятельно требует сегодня сделать эстетику не гостьей на уроке, а эффективным средством превращения ученика в чувственного, гуманного, творческого человека.