то, что он о себе думает, в числителе – то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь".
Лев Толстой
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Дроби
Содержание
- 1. Дроби
- 2. СОДЕРЖАНИЕ Понятие дроби
- 3. Понятие дроби Дробь - форма представления математических величин
- 4. Виды дробейОбыкновенные дроби;Правильные и неправильные дроби;Смешанные дроби;Составные дроби;Десятичные дроби;
- 5. Обыкновенные дроби Обыкновенная (или простая) дробь
- 6. Правильные и неправильные дроби Правильной называется дробь, у
- 7. Смешанные дроби Дробь, записанная в виде целого числа
- 8. Составные дроби Составной дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт. или
- 9. Десятичные дроби Десятичной дробью называют позиционную запись нецелого числа. Чаще всего употребляется десятичная система счисления.
- 10. Основное свойство дроби Если числитель
- 11. Действия над дробямиСложение ВычитаниеСравнениеУмножениеДеление
- 12. Сложение Чтобы сложить две дроби, следует привести
- 13. Вычитание Чтобы вычесть две дроби, следует привести их
- 14. Сравнение Чтобы сравнить две обыкновенные дроби, следует привести
- 15. Слайд 15
- 16. Умножение Произведение двух дробей равно дроби, числитель
- 17. ДелениеЧтобы разделить одну обыкновенную дробь на другую, надо умножить первую на дробь, обратную второй:
- 18. Понятие рационального числа Рациональное число (лат. ratio —
- 19. Множество рациональных чисел Множество рациональных чисел обозначается Q
- 20. Свойства рациональных чиселУпорядоченность Для любых рациональных чисел a
- 21. Два неположительных числа a и b связаны
- 22. 2. Операция сложения Для любых рациональных чисел
- 23. 3. Операция умножения Для любых рациональных чисел a
- 24. Правило умножения имеет следующий вид:
- 25. 4.Транзитивность отношения порядка Для любой тройки рациональных чисел
- 26. 5.Коммутативность сложения От перемены мест рациональных слагаемых сумма не меняется.
- 27. 6. Ассоциативность сложения Порядок сложения трёх рациональных чисел не влияет на результат.
- 28. 7. Наличие нуля Существует рациональное число 0, которое сохраняет любое другое рациональное число при суммировании.
- 29. 8. Наличие противоположных чисел Любое рациональное число
- 30. 9. Коммутативность умножения От перемены мест рациональных множителей произведение не меняется.
- 31. 10. Ассоциативность умножения Порядок перемножения трёх рациональных чисел не влияет на результат.
- 32. 11. Наличие единицы Существует рациональное число 1, которое сохраняет любое другое рациональное число при умножении.
- 33. 12. Наличие обратных чисел Любое ненулевое рациональное
- 34. 13. Дистрибутивность умножения относительно сложения Операция умножения согласована с операцией сложения посредством распределительного закона:
- 35. 14. Связь отношения порядка с операцией сложения
- 36. 15. Связь отношения порядка с операцией умножения Левую
- 37. 16. Аксиома Архимеда Каково бы ни было
СОДЕРЖАНИЕ Понятие дроби Виды дробей Основное свойство дроби Действия над дробями Понятие рационального числа Множество рациональных чисел Свойства рациональных чисел
Слайд 2СОДЕРЖАНИЕ
Понятие дроби
Виды дробей
Основное свойство дроби
Действия над дробями
Понятие рационального числа
Множество рациональных чисел
Свойства рациональных чисел
Действия над дробями
Понятие рационального числа
Множество рациональных чисел
Свойства рациональных чисел
Слайд 3Понятие дроби
Дробь - форма представления математических величин с помощью операции деления,
первоначально отражающая концепцию нецелых чисел, или долей.
Числовая дробь - отношение двух чисел.
Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата:
обыкновенные
десятичные
Числовая дробь - отношение двух чисел.
Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата:
обыкновенные
десятичные
Слайд 4Виды дробей
Обыкновенные дроби;
Правильные и неправильные дроби;
Смешанные дроби;
Составные дроби;
Десятичные дроби;
Слайд 5Обыкновенные дроби
Обыкновенная (или простая) дробь —запись рационального числа в
виде
или
Горизонтальная или косая черта обозначает операцию деления, порождающее данное число. Делимое называется числителем дроби, а делитель — знаменателем.
или
Горизонтальная или косая черта обозначает операцию деления, порождающее данное число. Делимое называется числителем дроби, а делитель — знаменателем.
Слайд 6Правильные и неправильные дроби
Правильной называется дробь, у которой модуль числителя меньше
модуля знаменателя.
Дробь, не являющаяся правильной, называется неправильной, и представляет рациональное число, по модулю большее или равное единице.
Дробь, не являющаяся правильной, называется неправильной, и представляет рациональное число, по модулю большее или равное единице.
Слайд 7Смешанные дроби
Дробь, записанная в виде целого числа и правильной дроби, называется
смешанной дробью и понимается как сумма этого числа и дроби.
Слайд 8Составные дроби
Составной дробью называется выражение, содержащее несколько горизонтальных (или реже —
наклонных) черт.
или
или
Слайд 9Десятичные дроби
Десятичной дробью называют позиционную запись нецелого числа.
Чаще всего
употребляется десятичная система счисления.
Слайд 10Основное свойство дроби
Если числитель и знаменатель данной
дроби умножить или разделить на одно и то же число, неравное нулю, то получится дробь, равная данной.
Слайд 12Сложение
Чтобы сложить две дроби, следует привести их к общему знаменателю.
Затем сложить числители, а знаменатель оставить без изменений:
При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.
При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.
Слайд 13Вычитание
Чтобы вычесть две дроби, следует привести их к общему знаменателю. Затем
вычесть числители, а знаменатель оставить без изменений:
При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
Слайд 14Сравнение
Чтобы сравнить две обыкновенные дроби, следует привести их к общему знаменателю
и сравнить числители получившихся дробей. Дробь с бо́льшим числителем будет больше.
и НОК(4, 5)=20
Приводим дроби к знаменателю 20
Следовательно:
и НОК(4, 5)=20
Приводим дроби к знаменателю 20
Следовательно:
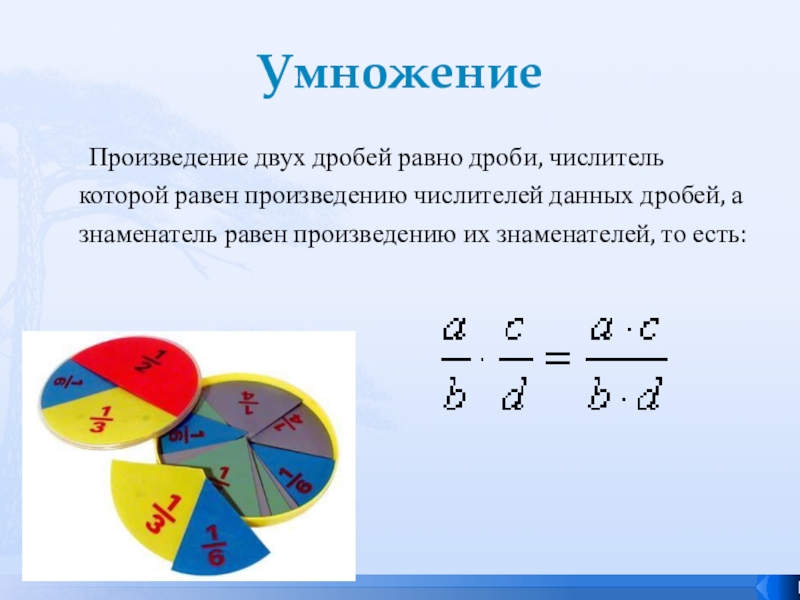
Слайд 16Умножение
Произведение двух дробей равно дроби, числитель которой равен произведению числителей
данных дробей, а знаменатель равен произведению их знаменателей, то есть:
Слайд 17Деление
Чтобы разделить одну обыкновенную дробь на другую, надо умножить первую на
дробь, обратную второй:
Слайд 18Понятие рационального числа
Рациональное число (лат. ratio — отношение, деление, дробь) —
число, представляемое несократимой обыкновенной дробью , где числитель m — целое число, а знаменатель n — натуральное число. Такую дробь следует понимать как результат деления m на n, даже если нацело разделить не удаётся.
Слайд 19Множество рациональных чисел
Множество рациональных чисел обозначается Q и может быть записано
в виде:
Множество рациональных чисел является естественным обобщением множества целых чисел
Множество рациональных чисел является естественным обобщением множества целых чисел
Слайд 20Свойства рациональных чисел
Упорядоченность
Для любых рациональных чисел a и b существует правило,
позволяющее однозначно идентифицировать между ними одно и только одно из трёх отношений: « < », « > » или « = ». Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа и
связаны тем же отношением, что и два целых числа и
связаны тем же отношением, что и два целых числа и
Слайд 21
Два неположительных числа a и b связаны тем же отношением, что
и два неотрицательных числа и
если же вдруг a неотрицательно, а b-отрицательно, то a > b.
если же вдруг a неотрицательно, а b-отрицательно, то a > b.
Слайд 22 2. Операция сложения
Для любых рациональных чисел a и b существует
так называемое правило суммирования, которое ставит им в соответствие некоторое рациональное число c. При этом само число c называется суммой чисел a и b и обозначается (a+b), а процесс отыскания такого числа называется суммированием. Правило суммирования имеет следующий вид:
Слайд 23 3. Операция умножения
Для любых рациональных чисел a и b существует так
называемое правило умножения, которое ставит им в соответствие некоторое рациональное число c.
При этом само число c называется произведением чисел a и b и обозначается,
а процесс отыскания такого числа также называется умножением .
При этом само число c называется произведением чисел a и b и обозначается,
а процесс отыскания такого числа также называется умножением .
Слайд 25 4.Транзитивность отношения порядка
Для любой тройки рациональных чисел a, b и c
если a меньше b и b меньше c, то a меньше c, а если a равно b и b равно c, то a равно c.
Слайд 27 6. Ассоциативность сложения
Порядок сложения трёх рациональных чисел не влияет на
результат.
Слайд 28 7. Наличие нуля
Существует рациональное число 0, которое сохраняет любое другое
рациональное число при суммировании.
Слайд 29 8. Наличие противоположных чисел
Любое рациональное число имеет противоположное рациональное число,
при суммировании с которым даёт 0.
Слайд 30 9. Коммутативность умножения
От перемены мест рациональных множителей произведение не меняется.
Слайд 31 10. Ассоциативность умножения
Порядок перемножения трёх рациональных чисел не влияет на
результат.
Слайд 32 11. Наличие единицы
Существует рациональное число 1, которое сохраняет любое другое
рациональное число при умножении.
Слайд 33 12. Наличие обратных чисел
Любое ненулевое рациональное число имеет обратное рациональное
число, умножение на которое даёт 1.
Слайд 34 13. Дистрибутивность умножения относительно сложения
Операция умножения согласована с операцией сложения посредством
распределительного закона:
Слайд 35 14. Связь отношения порядка с операцией сложения
К левой и правой
частям рационального неравенства можно прибавлять одно и то же рациональное число.
Слайд 36 15. Связь отношения порядка с операцией умножения
Левую и правую части рационального
неравенства можно умножать на одно и то же положительное рациональное число.
Слайд 37 16. Аксиома Архимеда
Каково бы ни было рациональное число a, можно
взять столько единиц, что их сумма превзойдёт a.