Бондаренко Т.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Числа Фибоначчи
Содержание
- 1. Числа Фибоначчи
- 2. Леонардо Пизанский (1170-1250)Первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибоначчи.
- 3. Книга-энциклопедия В 1202 г. появилась на свет знаменитая «Книга
- 4. В книге рассматривался весьма обширный круг вопросов:индусская
- 5. Числа ФибоначчиЧисла Фибоначчи или Последовательность Фибоначчи - числовая последовательность, обладающая рядом свойств.
- 6. Но как же Леонардо Фибоначчи вывел свою
- 7. Слайд 7
- 8. Слайд 8
- 9. Ряд Фибоначчи
- 10. Свойства чисел ФибоначчиЭта последовательность обладает рядом замечательных
- 11. Свойства чисел Фибоначчи2. Отношение каждого числа к
- 12. Свойства чисел Фибоначчи3. Отношение каждого числа ряда
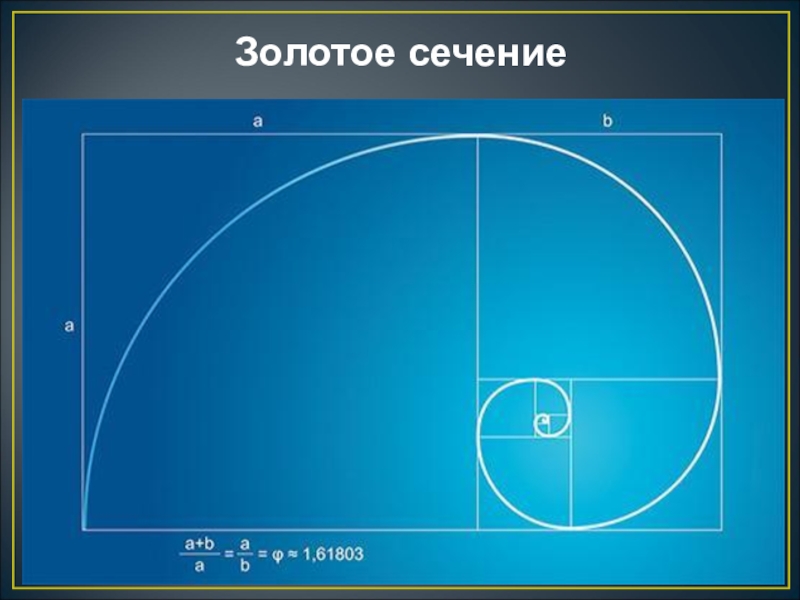
- 13. Золотое сечение
- 14. Слайд 14
- 15. Пропорции человеческого тела
- 16. Числа Фибоначчи в психологии0 – начала отсчета
- 17. ЗАКЛЮЧЕНИЕРяд Фибоначчи мог бы остаться только математическим
Леонардо Пизанский (1170-1250)Первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибоначчи.
Слайд 1Числа Фибоначчи
Выполнено учеником 11а класса Маленьких Алексеем под руководством учителя математики
Слайд 2Леонардо Пизанский (1170-1250)
Первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибоначчи.
Слайд 3Книга-энциклопедия
В 1202 г. появилась на свет знаменитая «Книга абака» Леонардо Пизанского крупнейшего европейского математика
эпохи Средневековья.
В ней подробно разъяснялись не только азы науки о числах и действиях над ними, но и основы учения об уравнениях, т.е. алгебры.
В ней подробно разъяснялись не только азы науки о числах и действиях над ними, но и основы учения об уравнениях, т.е. алгебры.
Слайд 4В книге рассматривался весьма обширный круг вопросов:
индусская система нумерации;
правила действий над
целыми числами;
дроби и смешанные числа;
разложение чисел на простые множители;
признаки делимости;
учение об иррациональных величинах;
способы приближенного вычисления квадратных и кубических корней;
свойства пропорции;
арифметическая и геометрическая прогрессии;
линейные уравнения и их системы.
Также отдельная глава была посвящена квадратным уравнениям и геометрическим задачам на применение теоремы Пифагора.
дроби и смешанные числа;
разложение чисел на простые множители;
признаки делимости;
учение об иррациональных величинах;
способы приближенного вычисления квадратных и кубических корней;
свойства пропорции;
арифметическая и геометрическая прогрессии;
линейные уравнения и их системы.
Также отдельная глава была посвящена квадратным уравнениям и геометрическим задачам на применение теоремы Пифагора.
Слайд 5Числа Фибоначчи
Числа Фибоначчи или Последовательность Фибоначчи - числовая последовательность, обладающая рядом
свойств.
Слайд 6
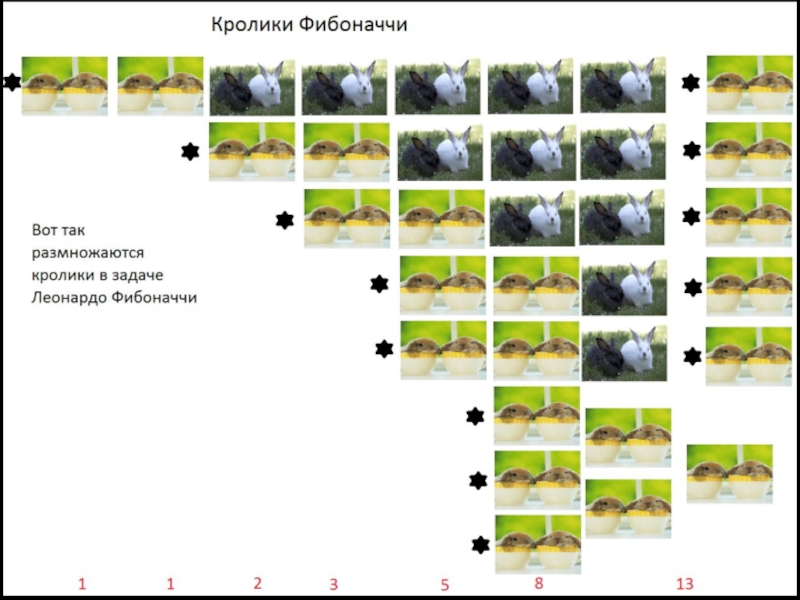
Но как же Леонардо Фибоначчи вывел свою последовательность? Причиной тому служит
одна из задач «Книги об абаке». Она гласит: «Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения».
Слайд 10Свойства чисел Фибоначчи
Эта последовательность обладает рядом замечательных свойств.
Каждое следующее число, начиная
с третьего, равно сумме двух предыдущих.
3+5=8 13+21=34
3+5=8 13+21=34
Слайд 11Свойства чисел Фибоначчи
2. Отношение каждого числа к последующему при увеличении порядкового
номера всё более и более стремится к 0.618
13:8=1.625
34:21=1.619
13:8=1.625
34:21=1.619
Слайд 12Свойства чисел Фибоначчи
3. Отношение каждого числа ряда к предыдущему стремится к
1.618
13:24=0.619
21:34=0.618
13:24=0.619
21:34=0.618
Слайд 16Числа Фибоначчи в психологии
0 – начала отсчета – ребенок родился. У
него еще отсутствуют мышление, чувства, воображение. Он – начало новой жизни, новой гармонии;
1 – ребенок овладел ходьбой и осваивает ближайшее окружение;
2 - понимает речь и действует, пользуясь словесными указаниями;
3 – начинает говорить, задает вопросы;
5 – «возраст грации» – гармония психомоторики, памяти, воображения и чувств;
8 – на передний план выходят чувства;
13 – начинает работать механизм таланта;
21 – механизм творчества приблизился к состоянию;
34 – гармония мышления, чувств, воображения и психомоторики: рождается способность к гениальной работе;
55 – в этом возрасте, при условии сохраненной гармонии души и тела, человек готов стать творцом. И так далее…
1 – ребенок овладел ходьбой и осваивает ближайшее окружение;
2 - понимает речь и действует, пользуясь словесными указаниями;
3 – начинает говорить, задает вопросы;
5 – «возраст грации» – гармония психомоторики, памяти, воображения и чувств;
8 – на передний план выходят чувства;
13 – начинает работать механизм таланта;
21 – механизм творчества приблизился к состоянию;
34 – гармония мышления, чувств, воображения и психомоторики: рождается способность к гениальной работе;
55 – в этом возрасте, при условии сохраненной гармонии души и тела, человек готов стать творцом. И так далее…
Слайд 17ЗАКЛЮЧЕНИЕ
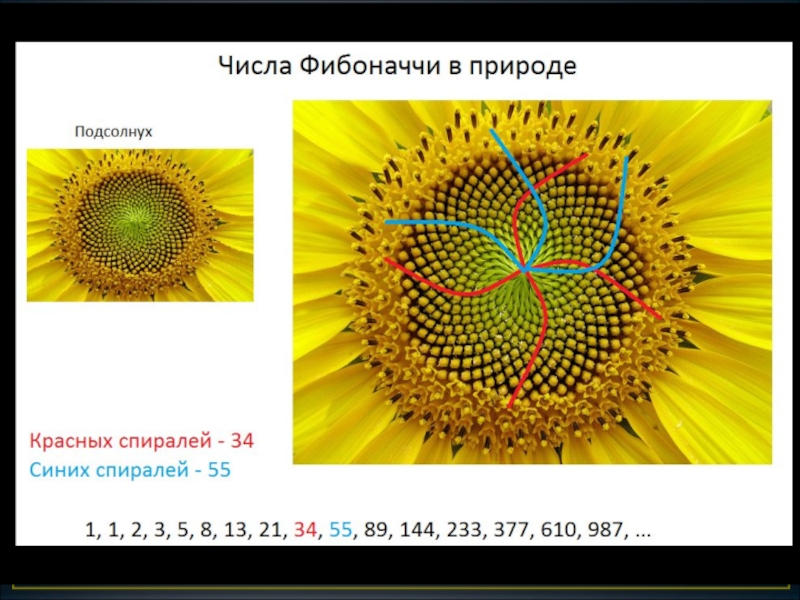
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не
то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве и архитектуре, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
Таким образом, суммарной последовательностью Фибоначчи легко можно трактовать закономерность проявлений Золотых чисел, встречаемых в природе. Эти законы действуют в независимости от нашего знания, от чьего-то желания принимать или не принимать их.