- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задача ЕГЗ-18. Логика на множествах в декартовой системе координат.
Содержание
- 1. Задача ЕГЗ-18. Логика на множествах в декартовой системе координат.
- 2. 287. Укажите наименьшее целое значение А, при
- 3. 312. Укажите наибольшее целое значение А, при
- 4. 332. Укажите наибольшее целое значение А, при
- 5. 294. Укажите наименьшее целое значение А, при
- 6. 304. Укажите наибольшее целое значение А, при
- 7. 314. Укажите наименьшее целое значение А, при
- 8. 341. Укажите наименьшее целое значение А, при
Слайд 1Логика на множествах
ЕГЭ 18
Множества точек в декартовой системе координат
Калинина О.Е.
МОУ «Гимназия
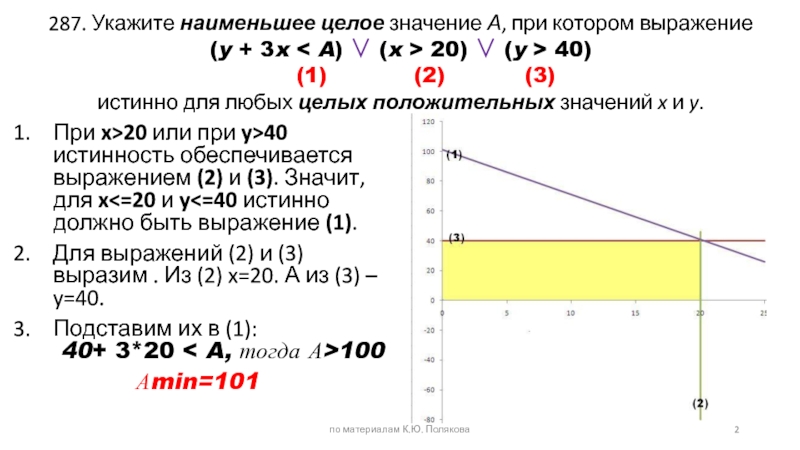
Слайд 2287. Укажите наименьшее целое значение А, при котором выражение (y + 3x
При x>20 или при y>40 истинность обеспечивается выражением (2) и (3). Значит, для x<=20 и y<=40 истинно должно быть выражение (1).
Для выражений (2) и (3) выразим . Из (2) x=20. А из (3) – y=40.
Подставим их в (1):
40+ 3*20 < A, тогда А>100
Аmin=101
по материалам К.Ю. Полякова
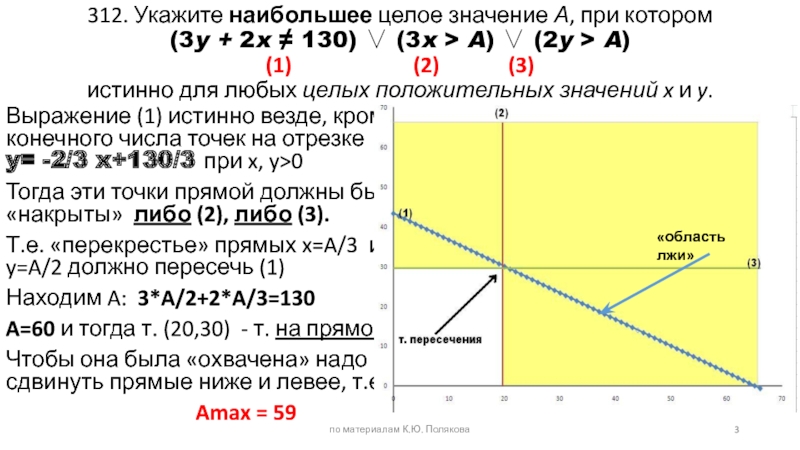
Слайд 3312. Укажите наибольшее целое значение А, при котором (3y + 2x
Выражение (1) истинно везде, кроме конечного числа точек на отрезке
y= -2/3 x+130/3 при x, y>0
Тогда эти точки прямой должны быть «накрыты» либо (2), либо (3).
Т.е. «перекрестье» прямых x=A/3 и y=A/2 должно пересечь (1)
Находим A: 3*A/2+2*A/3=130
A=60 и тогда т. (20,30) - т. на прямой
Чтобы она была «охвачена» надо сдвинуть прямые ниже и левее, т.е.
Amax = 59
по материалам К.Ю. Полякова
«область лжи»
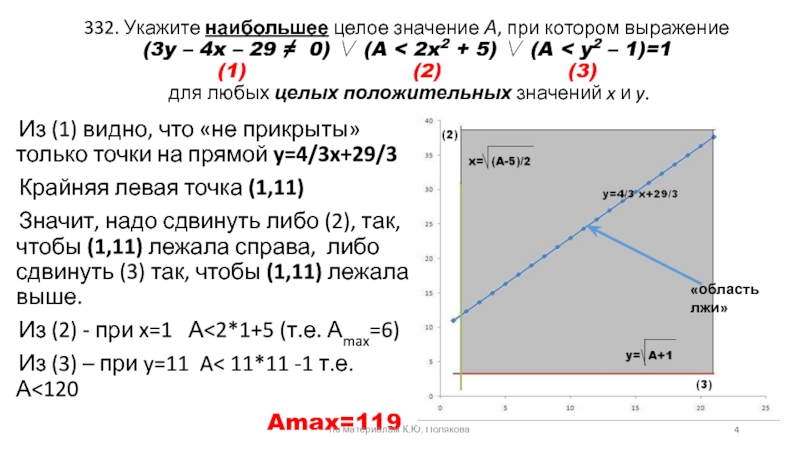
Слайд 4332. Укажите наибольшее целое значение А, при котором выражение (3y – 4x
Из (1) видно, что «не прикрыты» только точки на прямой y=4/3x+29/3
Крайняя левая точка (1,11)
Значит, надо сдвинуть либо (2), так, чтобы (1,11) лежала справа, либо сдвинуть (3) так, чтобы (1,11) лежала выше.
Из (2) - при x=1 А<2*1+5 (т.е. Аmax=6)
Из (3) – при y=11 A< 11*11 -1 т.е. А<120
Amax=119
по материалам К.Ю. Полякова
«область лжи»
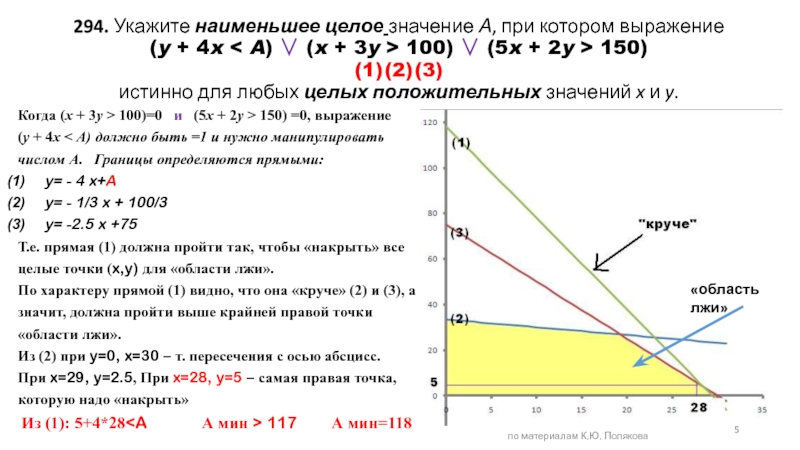
Слайд 5294. Укажите наименьшее целое значение А, при котором выражение (y + 4x
по материалам К.Ю. Полякова
Когда (x + 3y > 100)=0 и (5x + 2y > 150) =0, выражение
(y + 4x < A) должно быть =1 и нужно манипулировать числом А. Границы определяются прямыми: «круче» «область лжи»
y= - 4 x+A
y= - 1/3 x + 100/3
y= -2.5 x +75
Т.е. прямая (1) должна пройти так, чтобы «накрыть» все целые точки (x,y) для «области лжи».
По характеру прямой (1) видно, что она «круче» (2) и (3), а значит, должна пройти выше крайней правой точки «области лжи».
Из (2) при y=0, x=30 – т. пересечения с осью абсцисс.
При x=29, y=2.5, При x=28, y=5 – самая правая точка, которую надо «накрыть»
Из (1): 5+4*28 117 А мин=118
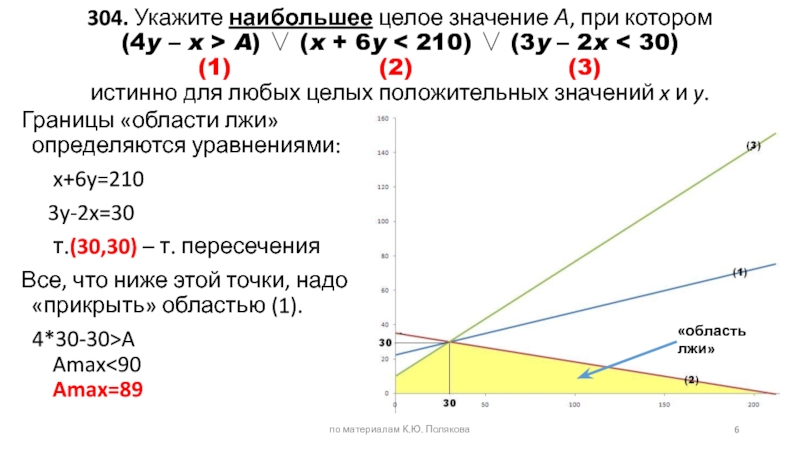
Слайд 6304. Укажите наибольшее целое значение А, при котором (4y – x
Границы «области лжи» определяются уравнениями:
x+6y=210
3y-2x=30
т.(30,30) – т. пересечения
Все, что ниже этой точки, надо «прикрыть» областью (1).
4*30-30>A
Amax<90
Amax=89
по материалам К.Ю. Полякова
«область лжи»
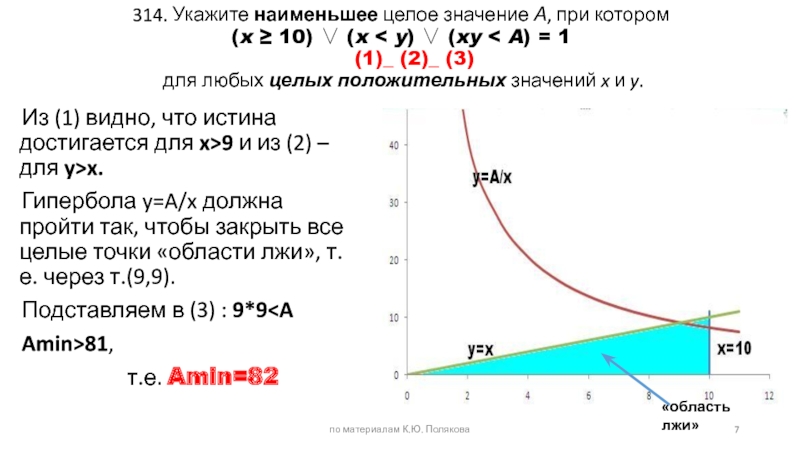
Слайд 7314. Укажите наименьшее целое значение А, при котором (x 10)
Из (1) видно, что истина достигается для x>9 и из (2) – для y>x. по материалам К.Ю. Полякова «область лжи»
Гипербола y=A/x должна пройти так, чтобы закрыть все целые точки «области лжи», т.е. через т.(9,9).
Подставляем в (3) : 9*9
т.е. Amin=82
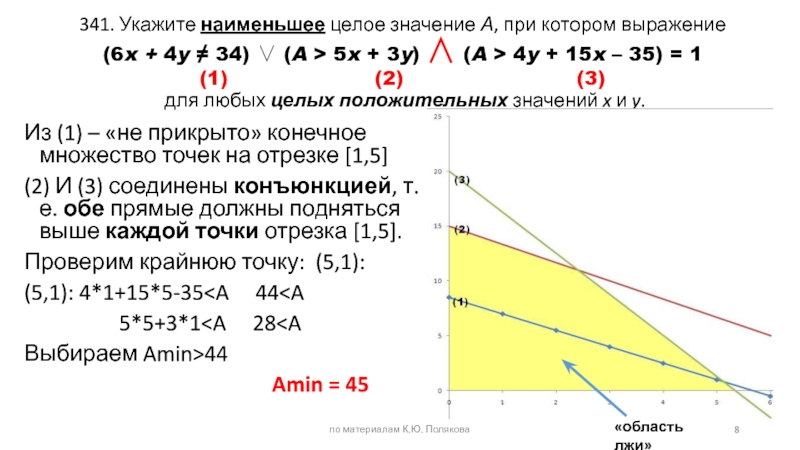
Слайд 8341. Укажите наименьшее целое значение А, при котором выражение (6x + 4y
Из (1) – «не прикрыто» конечное
множество точек на отрезке [1,5] по материалам К.Ю. Полякова «область лжи»
(2) И (3) соединены конъюнкцией, т.е. обе прямые должны подняться выше каждой точки отрезка [1,5].
Проверим крайнюю точку: (5,1):
(5,1): 4*1+15*5-35 5*5+3*1Выбираем Amin>44
Amin = 45