- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок Презентация по теме Транспортная задача
Содержание
- 1. Урок Презентация по теме Транспортная задача
- 2. Транспортная задачаЗадача составления плана перевозок от поставщиков
- 3. Постановка задачиИзвестно, что на складах имеется
- 4. Математическая модель
- 5. Анализ задачиСуммарные затраты на перевозки Z
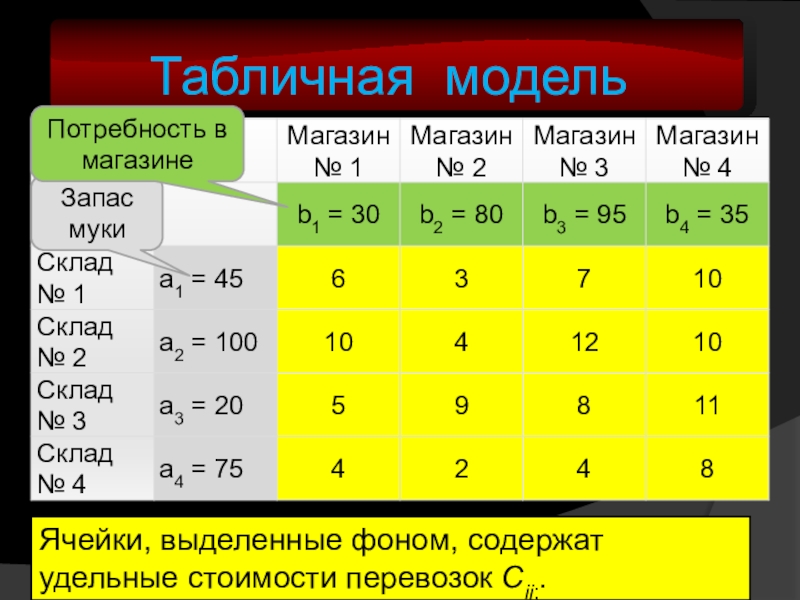
- 6. Табличная модельЯчейки, выделенные фоном, содержат удельные стоимости перевозок Cij;.Запас мукиПотребность в магазине
- 7. Математический анализПроверим замкнутость моделиДля этого просуммируем все
- 8. Математический анализВесь груз со складов должен быть
- 9. Математическая модельZ = С11 Х11 +...
- 10. Математическая модель Ограничения:Аi >=0Bi >=0Решение с помощью
- 11. Компьютерная модель решаем в Excel!Работа 3.19 (Семакин)
Слайд 1Транспортная задача
Информатика и ИКТ 11 класс
§ 3.4.2
Подготовил учитель информатик
МОУ «Школа-лицей
Успаленко Игорь Николаевич
Слайд 2Транспортная задача
Задача составления плана перевозок от поставщиков к потребителям с помощью
Составленный план должен обеспечивать выполнение таких условий, как:
• полное удовлетворение спроса потребителей;
• вывоз всей продукции от поставщика;
• минимизация транспортных затрат.
Слайд 3Постановка задачи
Известно, что на складах имеется запас муки в количестве
А магазины имеют потребность в этом товаре в количестве 30, 80, 95, 35 мешков.
Перевозку груза надо организовать таким образом, чтобы суммарные затраты на перевозки были минимальными.
Слайд 4Математическая модель
В
Потребность в этом грузе в n пунктах назначения (магазинах) В1, В2, ..., Вп составляет bl b2, ..., bп соответственно.
Будем считать, что сумма запасов на складах равна суммарным потребностям в магазинах, т.е.
Такая модель называется замкнутой.
Слайд 5Анализ задачи
Суммарные затраты на перевозки Z определяются следующим образом: необходимо
Суммарные затраты являются целевой функцией.
Слайд 6Табличная модель
Ячейки, выделенные фоном, содержат удельные стоимости перевозок Cij;.
Запас муки
Потребность в
Слайд 7Математический анализ
Проверим замкнутость модели
Для этого просуммируем все запасы муки на складах:
Найдем суммарные потребности магазинов в муке: 30 + 80 + 95 + 35 = 240.
Ограничения
Слайд 8Математический анализ
Весь груз со складов должен быть вывезен.
удовлетворению спроса магазинов
удовлетворению спроса магазинов отвечает выполнение системы уравнений:
удовлетворяет спроса магазинов
Вывоз всего груза со складов достигается при выполнении системы уравнений:
Слайд 9Математическая модель
Z = С11 Х11 +... +С14 Х14 +С21
удовлетворению спроса магазинов отвечает выполнение системы уравнений:
удовлетворению спроса магазинов отвечает выполнение системы уравнений:
Среди этих решений интерес представляют неотрицательные решения, при которых суммарные затраты по всем маршрутам будут минимальны, т. е. целевая функция может быть представлена следующим образом:
Слайд 10Математическая модель
Ограничения:
Аi >=0
Bi >=0
Решение с помощью электронных таблиц
Первое ограничение
второе – по уровню запасов