- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок, Презентация Алгоритм. Свойства алгоритма (9-11 классы)
Содержание
- 1. Урок, Презентация Алгоритм. Свойства алгоритма (9-11 классы)
- 2. Понятие алгоритмаАлгоритм - точное предписание исполнителю совеpшить
- 3. Основными свойствами алгоритма являются: дискретность (прерывность, раздельность)-
- 4. Основными свойствами алгоритма являются: массовость - алгоритм
- 5. Способы записи алгоритмовсловесный, формульно-словесный, графический,язык операторных схем,алгоритмический язык.
- 6. Графический (блок-схемный) способ записи алгоритмовЧто такое блок-схема?Блок-схемой
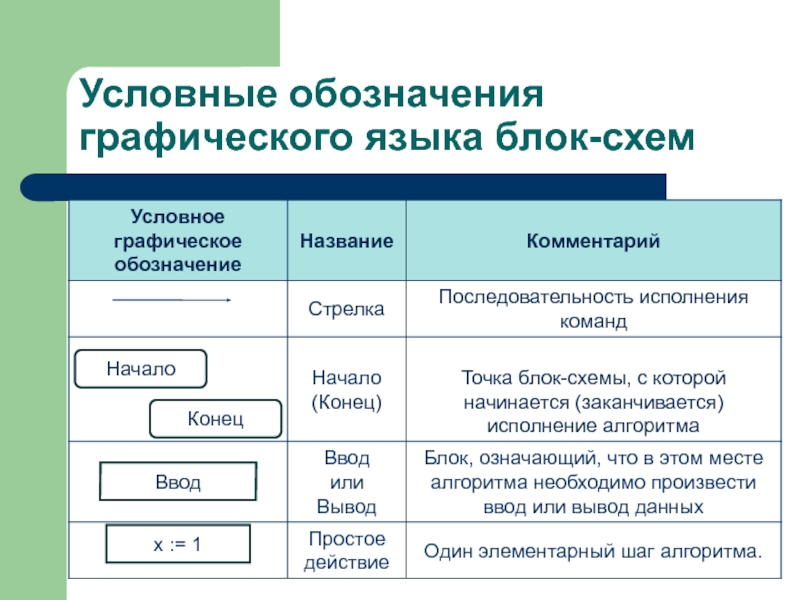
- 7. Условные обозначения графического языка блок-схемНачалоКонецВводх := 1
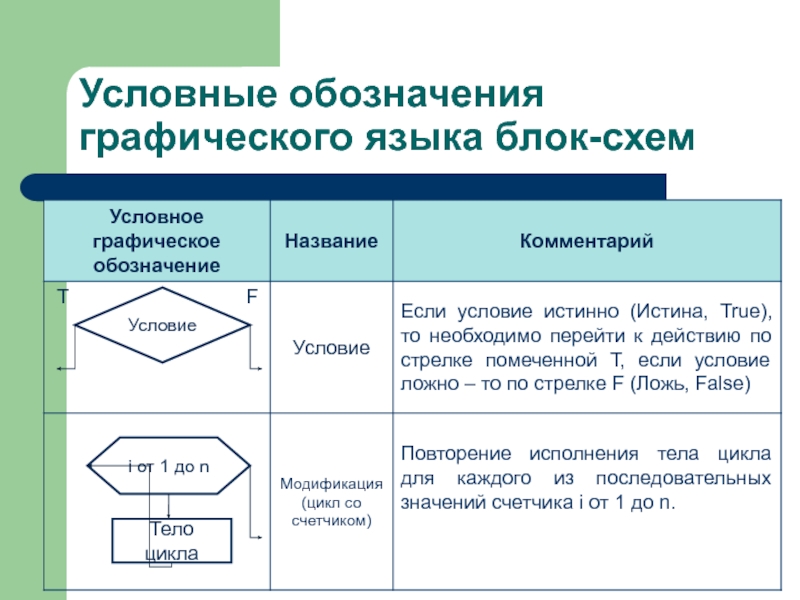
- 8. Условные обозначения графического языка блок-схемУсловиеi от 1 до nТело цикла
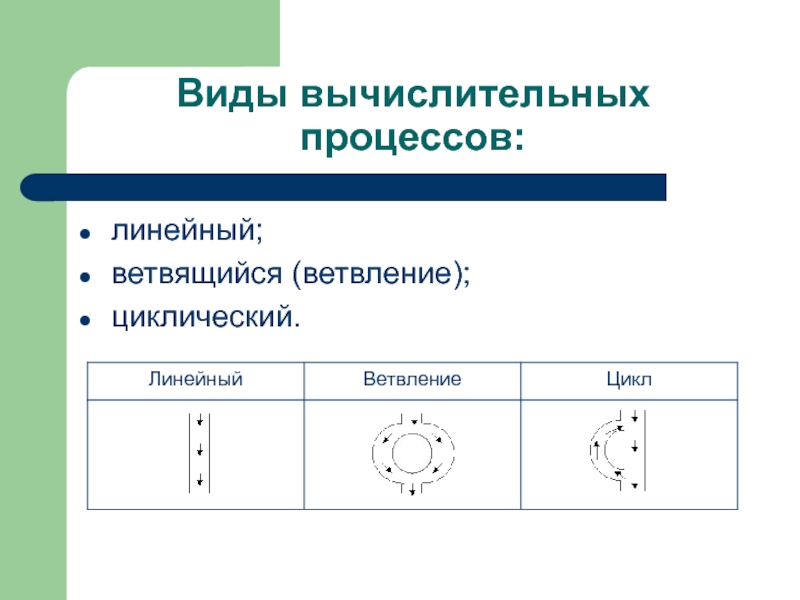
- 9. Виды вычислительных процессов: линейный; ветвящийся (ветвление); циклический.
- 10. Линейный алгоритмЛинейным называется такой вычислительный процесс, при
- 11. ВетвлениеРазветвляющийся алгоритм - содержащий хотя бы одно
- 12. ЦиклическиеЦиклический алгоритм – алгоритм, предусматривающий многократное повторение
- 13. Цикл программыЭто последовательность команд (серия, тело цикла),
- 14. Требования, предъявляемые к алгоритму. Правило 1.При построении
- 15. Правило 2Для работы алгоритма требуется память.В памяти
- 16. Правило 3Дискретность. Алгоритм строится из отдельных шагов
- 17. Правило 5. Сходимость (результативность). После каждого шага
- 18. Пример 1. Линейный алгоритмСоставить блок-схему алгоритма, решающего
- 19. Пример 2. Алгоритмы с ветвлениемСоставить блок-схему решения
- 20. Пример 3. Линейный алгоритмСоставить блок-схему решения следующей
- 21. Пример 4. Решение квадратного уравненияСоставить словесный алгоритм
- 22. Домашнее задание. Составьте алгоритмы для решения следующих
Понятие алгоритмаАлгоритм - точное предписание исполнителю совеpшить определенную последовательность действий для достижения поставленной цели за конечное число шагов. Первоначально под алгоритмом понимали только правила выполнения четырех арифметических действий над числами.
Слайд 2Понятие алгоритма
Алгоритм - точное предписание исполнителю совеpшить определенную последовательность действий для
достижения поставленной цели за конечное число шагов.
Первоначально под алгоритмом понимали только правила выполнения четырех арифметических действий над числами.
Первоначально под алгоритмом понимали только правила выполнения четырех арифметических действий над числами.
Слайд 3Основными свойствами алгоритма являются:
дискретность (прерывность, раздельность)- алгоритм должен представлять процесс
решения задачи как последовательное выполнение простых шагов
определенность - каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола;
определенность - каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола;
Слайд 4Основными свойствами алгоритма являются:
массовость - алгоритм решения задачи разрабатывается в
общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными;
результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.
результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.
Слайд 5Способы записи алгоритмов
словесный,
формульно-словесный,
графический,
язык операторных схем,
алгоритмический язык.
Слайд 6Графический (блок-схемный) способ записи алгоритмов
Что такое блок-схема?
Блок-схемой называется графическое изображение логической
структуры алгоритма, в котором каждый этап процесса обработки информации представляется в виде геометрических символов (блоков), имеющих определенную конфигурацию в зависимости от характера выполняемых операций.
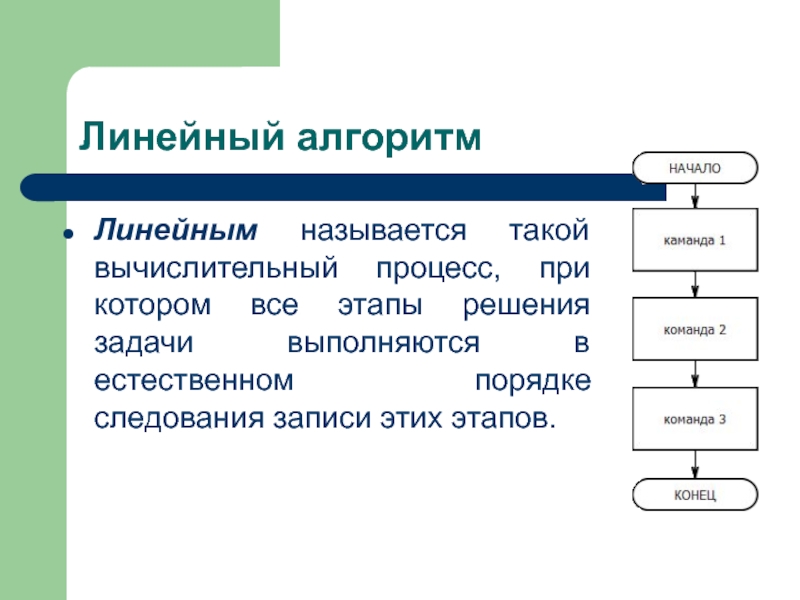
Слайд 10Линейный алгоритм
Линейным называется такой вычислительный процесс, при котором все этапы решения
задачи выполняются в естественном порядке следования записи этих этапов.
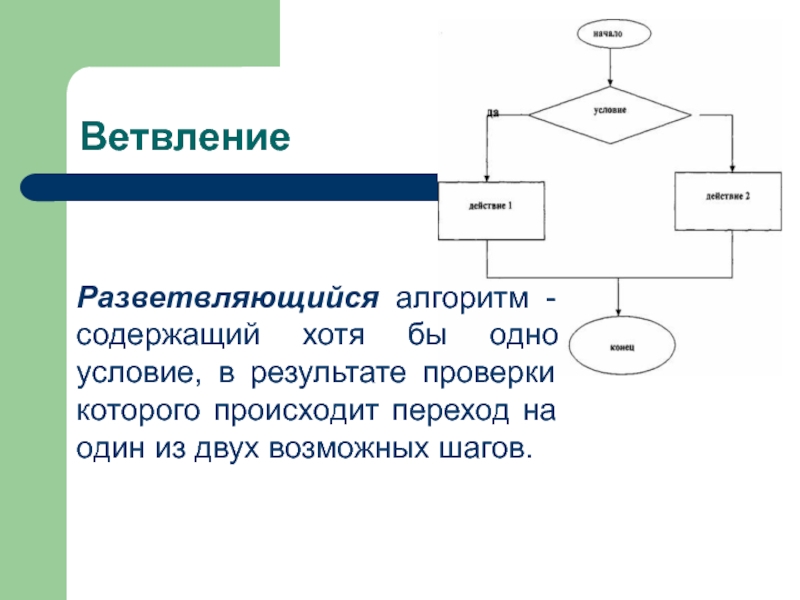
Слайд 11Ветвление
Разветвляющийся алгоритм - содержащий хотя бы одно условие, в результате проверки
которого происходит переход на один из двух возможных шагов.
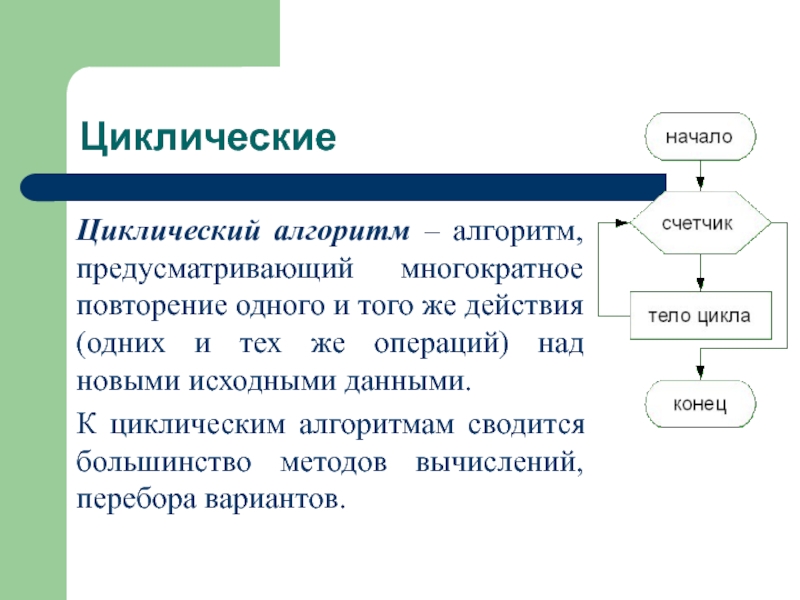
Слайд 12Циклические
Циклический алгоритм – алгоритм, предусматривающий многократное повторение одного и того же
действия (одних и тех же операций) над новыми исходными данными.
К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов.
К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов.
Слайд 13Цикл программы
Это последовательность команд (серия, тело цикла), которая может выполняться многократно
(для новых исходных данных) до удовлетворения некоторого условия.
Слайд 14Требования, предъявляемые к алгоритму. Правило 1.
При построении алгоритма необходимо задать множество
объектов, с которыми будет работать алгоритм.
Алгоритм приступает к работе с некоторым набором данных, которые называются входными, и в результате своей работы выдает данные, которые называются выходными. Таким образом, алгоритм преобразует входные данные в выходные.
Пока мы не имеем формализованных входных данных, мы не можем построить алгоритм.
Алгоритм приступает к работе с некоторым набором данных, которые называются входными, и в результате своей работы выдает данные, которые называются выходными. Таким образом, алгоритм преобразует входные данные в выходные.
Пока мы не имеем формализованных входных данных, мы не можем построить алгоритм.
Слайд 15Правило 2
Для работы алгоритма требуется память.
В памяти размещаются входные данные, с
которыми алгоритм начинает работать, промежуточные и выходные данные, которые являются результатом работы алгоритма.
Память является дискретной, т.е. состоящей из отдельных ячеек. Поименованная ячейка памяти носит название переменной.
Память является дискретной, т.е. состоящей из отдельных ячеек. Поименованная ячейка памяти носит название переменной.
Слайд 16Правило 3
Дискретность.
Алгоритм строится из отдельных шагов (действий, операций, команд). Множество
шагов, из которых составлен алгоритм, конечно.
Слайд 17Правило 5. Сходимость (результативность).
После каждого шага необходимо указывать, какой шаг
выполняется следующим, либо давать команду остановки.
Алгоритм должен завершать работу после конечного числа шагов. При этом необходимо указать, что считать результатом работы алгоритма.
Алгоритм должен завершать работу после конечного числа шагов. При этом необходимо указать, что считать результатом работы алгоритма.
Правило 4. Детерминированность.
Слайд 18Пример 1. Линейный алгоритм
Составить блок-схему алгоритма, решающего следующую задачу: даны три
вещественных положительных числа a, b и c. Найти площадь треугольника, стороны которого равны a, b и c.
Слайд 19Пример 2. Алгоритмы с ветвлением
Составить блок-схему решения следующей задачи: даны значения
двух действительных переменных a и b.
Найти наибольшее значение из a и b.
Найти наибольшее значение из a и b.
Слайд 20Пример 3. Линейный алгоритм
Составить блок-схему решения следующей задачи.
Даны значения действительных
переменных b и c. Решить линейное уравнение bx+c=0.
Слайд 21Пример 4. Решение квадратного уравнения
Составить словесный алгоритм и блок-схему решения следующей
задачи:
Даны значения действительных переменных a, b и c, причем a≠0.
Решить уравнение ax2+bx+c=0.
Даны значения действительных переменных a, b и c, причем a≠0.
Решить уравнение ax2+bx+c=0.
Слайд 22Домашнее задание.
Составьте алгоритмы для решения следующих задач:
Даны значения двух действительных переменных
a и b. Обменять местами их значения, не используя дополнительные переменные.
Даны значения трех действительных переменных a, b и c. Найти наибольшее значение из a, b и c.
Даны значения действительных переменных a, b и c. Решить уравнение ax2+bx+c=0.
Даны значения трех действительных переменных a, b и c. Найти наибольшее значение из a, b и c.
Даны значения действительных переменных a, b и c. Решить уравнение ax2+bx+c=0.