- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок Информационные оптимизационные модели_11 класс (профильный)
Содержание
- 1. Урок Информационные оптимизационные модели_11 класс (профильный)
- 2. Оптимизация – нахождение экстремума (максимума или минимума) целевой функции в некоторой области конечного мерного векторного пространства
- 3. Характерные черты задач ЛП: Показатель оптимальности представляет
- 4. Целевая функция при ограничениях
- 5. Допустимое решение – это совокупность чисел (план)
- 6. Задача: Фабрика производит два вида красок: первый
- 7. Задача: Изучение рынка сбыта показало, что суточный
- 8. Решение: Что является искомыми величинами задачи? (переменными)Какова
- 9. Решение: 1) - суточный
- 10. Решение: 3) Все ограничения задачи делятся на
- 11. Решение: Ограничение по суточному объему производства краски
- 12. Решение: Ограничение по суточному объему производства краски 1-го вида имеет содержательную формуИ математическую форму
- 13. Слайд 13
- 14. TitleLorem ipsum dolor sit amet, consectetuer adipiscing
- 15. Построение и исследование оптимизационной модели
- 16. П.1.6.1 – 1.6.3, стр. 68 – 74Домашнее задание
Оптимизация – нахождение экстремума (максимума или минимума) целевой функции в некоторой области конечного мерного векторного пространства
Слайд 1
Информационные оптимизационные модели
ОПТИМИЗАЦИОННОЕ МОДЕЛИРОВАНИЕ В ЭКОНОМИКЕ
Чудная Л.Г.
МБОУ СОШ №1 г. Нерюнгри
Слайд 2Оптимизация –
нахождение экстремума (максимума или минимума) целевой функции в некоторой
области конечного мерного векторного пространства
Слайд 3Характерные черты задач ЛП:
Показатель оптимальности представляет собой линейную функцию X
= ( );
Ограничительные условия, накладываемые на возможные решения, имеют вид линейных равенств или неравенств.
Ограничительные условия, накладываемые на возможные решения, имеют вид линейных равенств или неравенств.
Слайд 5Допустимое решение – это совокупность чисел (план) X = (
), удовлетворяющих ограничениям задачи.
Оптимальное решение – это план, при котором целевая функция принимает свое максимальное (минимальное) значение.
Оптимальное решение – это план, при котором целевая функция принимает свое максимальное (минимальное) значение.
Слайд 6Задача:
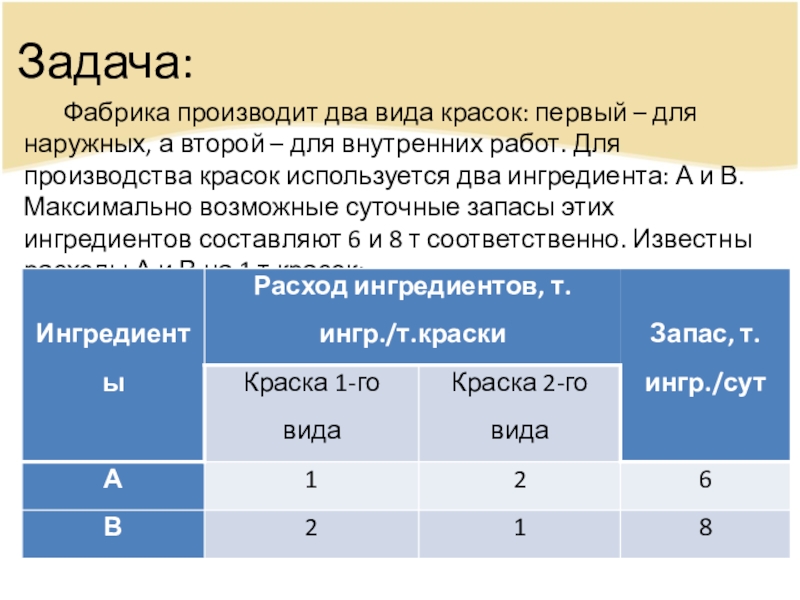
Фабрика производит два вида красок: первый – для наружных, а
второй – для внутренних работ. Для производства красок используется два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известны расходы А и В на 1 т красок:
Слайд 7Задача:
Изучение рынка сбыта показало, что суточный спрос на краску 2-го
вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, спрос на краску 2-го вида не превышает 2 т /сут. Оптовые цены 1 т красок равны: 3 т. руб. для краски 1-го вида и 2 т. руб. для краски 2-го вида. Найти какое количество краски каждого вида необходимо производить, чтобы доход от реализации продукции был максимальным.
Слайд 8Решение:
Что является искомыми величинами задачи? (переменными)
Какова цель решения, т.е. какой
параметр будет служить критерием оптимальности и в каком направлении должно изменяться значение этого параметра для достижения оптимальных результатов (max, min)?
Какие условия должны быть выполнены в отношении искомых величин? (записываются в виде системы равенств или неравенств, т.е. ограничений)
Какие условия должны быть выполнены в отношении искомых величин? (записываются в виде системы равенств или неравенств, т.е. ограничений)
Слайд 9Решение:
1) - суточный объем производства краски 1-го
вида,
- суточный объем производства краски 2-го вида,
2)
- суточный объем производства краски 2-го вида,
2)
Слайд 10Решение:
3) Все ограничения задачи делятся на три группы, обусловленные:
расходом
ингредиентов;
рыночным спросом на краску;
неотрицательностью объемов производства.
рыночным спросом на краску;
неотрицательностью объемов производства.
Слайд 11Решение:
Ограничение по суточному объему производства краски 1-го вида по сравнению
с объемом производства краски 2-го вида имеет содержательную форму
И математическую форму
И математическую форму
Слайд 12Решение:
Ограничение по суточному объему производства краски 1-го вида имеет содержательную
форму
И математическую форму
И математическую форму
Слайд 14Title
Lorem ipsum dolor sit amet, consectetuer adipiscing elit. Vivamus et magna.
Fusce sed sem sed magna suscipit egestas.
Lorem ipsum dolor sit amet, consectetuer adipiscing elit. Vivamus et magna. Fusce sed sem sed magna suscipit egestas.
Lorem ipsum dolor sit amet, consectetuer adipiscing elit. Vivamus et magna. Fusce sed sem sed magna suscipit egestas.