2014
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок информатики на тему: Кодирование информации. Системы счисления.
Содержание
- 1. Урок информатики на тему: Кодирование информации. Системы счисления.
- 2. КОДИРОВАНИЕ информации - представление информации в той
- 3. СИСТЕМЫ СЧИСЛЕНИЯ - способы кодирования числовой информации,
- 4. 1. Римская непозиционная система счисления.В ней семь
- 5. 2. Десятичная система счисления. Располагает только десятью
- 6. Основанием десятичной системы является десяток, и поэтому,
- 7. Двоичная система счисления. Эта система тоже является
- 8. Представим десятичное число 13 в двоичном коде.Для
- 9. Способ 2.Будем делить число 13 последовательно на
- 10. Обычно этот способ используют для представления больших
- 11. Перевод числа из двоичной системы счисления в
- 12. Основной недостаток двоичной системы
КОДИРОВАНИЕ информации - представление информации в той или иной стандартной форме. Например, письменность и арифметика - кодирование речи и числовой информации, музыку кодируют с помощью нот. Чтобы использовать числа их нужно как-то записывать и
Слайд 1Кодирование информации.
Системы счисления.
Урок информатики и ИКТ
Учитель: Кривенцов Л.А.
Первая квалификационная категория
Асино -
Слайд 2КОДИРОВАНИЕ информации - представление информации в той или иной стандартной форме. Например,
письменность и арифметика - кодирование речи и числовой информации, музыку кодируют с помощью нот.
Чтобы использовать числа их нужно как-то записывать и называть.
Самые первые системы нумерации возникли в Др. Египте и Месопотамии - применяли иероглифы
Слайд 3СИСТЕМЫ СЧИСЛЕНИЯ - способы кодирования числовой информации, т.е. способ записи чисел
с помощью некоторого алфавита, символы которого называют цифрами.
В древнем Вавилоне делили час на 60 мин., угол на 360 градусов, англосаксы начали делить год на 12 месяцев, сутки на два периода по 12 часов, продолжительность года 360 суток.
В древнем Вавилоне делили час на 60 мин., угол на 360 градусов, англосаксы начали делить год на 12 месяцев, сутки на два периода по 12 часов, продолжительность года 360 суток.
Слайд 41. Римская непозиционная система счисления.
В ней семь чисел обозначаются буквами:
1 —
I, 5 — V, 10 — X, 50 — L, 100 — С, 500 — D, 1000 — М,
а остальные числа записываются комбинациями этих букв.
а остальные числа записываются комбинациями этих букв.
Слайд 52. Десятичная система счисления.
Располагает только десятью цифрами —
0, 1,
2, 3, 4, 5, 6, 7, 8, 9
Является позиционной, а это означает, что значение каждой цифры числа определяется ее местом (позицией) в числе. Например, в числе 459 цифра 9 представляет единицы, цифра 5 — десятки, цифра 4 — сотни.
Является позиционной, а это означает, что значение каждой цифры числа определяется ее местом (позицией) в числе. Например, в числе 459 цифра 9 представляет единицы, цифра 5 — десятки, цифра 4 — сотни.
Слайд 6Основанием десятичной системы является десяток, и поэтому, например, число 459 можно
представить суммой:
459 = 400 + 50 + 9 = 4*102+5*101 +9*10°.
Если число имеет дробную часть, то добавляется сумма оснований 10 с отрицательными степенями. Например:
321,409 = 3*102+2*101+1*10°+4*10^-1+0*10^
-2+9*10^-3.
459 = 400 + 50 + 9 = 4*102+5*101 +9*10°.
Если число имеет дробную часть, то добавляется сумма оснований 10 с отрицательными степенями. Например:
321,409 = 3*102+2*101+1*10°+4*10^-1+0*10^
-2+9*10^-3.
Слайд 7Двоичная система счисления.
Эта система тоже является позиционной, но по основанию
2.
В нашем распоряжении только
две цифры - 0 и 1.
В нашем распоряжении только
две цифры - 0 и 1.
Слайд 8Представим десятичное число 13 в двоичном коде.
Для начала определим, 2 в
какой максимальной степени «входит» в число 13 и выпишем последовательно (не пропуская) все остальные степени числа 2, начиная с максимальной и заканчивая нулевой. Перед каждой «помещающейся» в число 13 степенью двойки поставим коэффициент 1 (присутствует), а перед «непомещающейся» — коэффициент 0 (отсутствует).
13¹º = 1*2³ + 1*2² +0*2¹ +1*2°= 8 + 4 + 0 + 1.
Теперь выпишем все коэффициенты, и так как число записывается в 1 байт, содержащий 8 бит, то дополним получившееся двоичное число недостающими нулями:
13¹º = 000011012
13¹º = 1*2³ + 1*2² +0*2¹ +1*2°= 8 + 4 + 0 + 1.
Теперь выпишем все коэффициенты, и так как число записывается в 1 байт, содержащий 8 бит, то дополним получившееся двоичное число недостающими нулями:
13¹º = 000011012
Слайд 9Способ 2.
Будем делить число 13 последовательно на 2 нацело и запоминать
остатки, в том числе и нулевые:
13 : 2 = 6 остаток 1
6:2 = 3 остаток 0
3:2 = 1 остаток 1
1:2 = 0 остаток 1
Выписав все остатки, начиная с последнего, получим двоичное представление числа:
1310 = 11012
13 : 2 = 6 остаток 1
6:2 = 3 остаток 0
3:2 = 1 остаток 1
1:2 = 0 остаток 1
Выписав все остатки, начиная с последнего, получим двоичное представление числа:
1310 = 11012
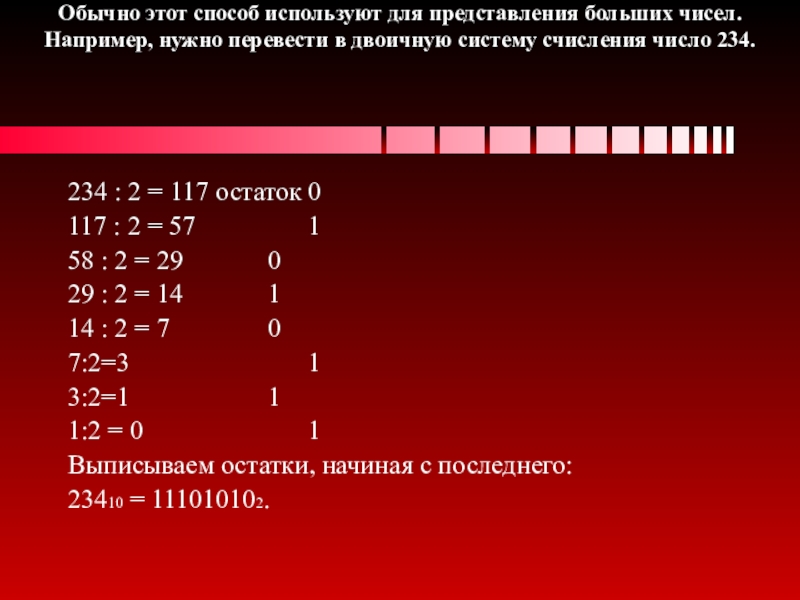
Слайд 10Обычно этот способ используют для представления больших чисел. Например, нужно перевести
в двоичную систему счисления число 234.
234 : 2 = 117 остаток 0
117 : 2 = 57 1
58 : 2 = 29 0
29 : 2 = 14 1
14 : 2 = 7 0
7:2=3 1
3:2=1 1
1:2 = 0 1
Выписываем остатки, начиная с последнего:
23410 = 111010102.
Слайд 11Перевод числа из двоичной системы счисления в десятичную.
Для начала расставим
над цифрами двоичного числа степени, начиная с нулевой справа налево.
Вспомнив, что ноли и единицы являются коэффициентами при степенях числа 2, запишем двоичное число в виде суммы:
1^5 1^4 1³ 1² 0¹ 1°2 = 1*2^5 + 1*2^4 + 1*2³ + 1*2² + 0*2¹ +1*2° = 32 + 16 + 8 + 4 +1= 6110.
Вспомнив, что ноли и единицы являются коэффициентами при степенях числа 2, запишем двоичное число в виде суммы:
1^5 1^4 1³ 1² 0¹ 1°2 = 1*2^5 + 1*2^4 + 1*2³ + 1*2² + 0*2¹ +1*2° = 32 + 16 + 8 + 4 +1= 6110.
Слайд 12 Основной недостаток двоичной системы состоит в том, что,
поскольку основание системы мало, для записи даже не очень больших чисел приходится использовать много знаков. Поэтому в современных компьютерах помимо двоичной системы счисления применяют и другие, более компактные по длине чисел системы, такие, как восьмеричная и шестнадцатеричная.