- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тренажер для проверки знаний, по теме: система счисления
Содержание
- 1. Тренажер для проверки знаний, по теме: система счисления
- 2. Системы счисленияПозиционные Непозиционные
- 3. Система счисления называется позиционной, если количественный эквивалент
- 4. Цифры 1234567890 сложились в Индии около 400
- 5. В позиционной системе счисления с основанием q
- 6. Aq =±(an–1 qn–1+ an–2 qn–2+…+
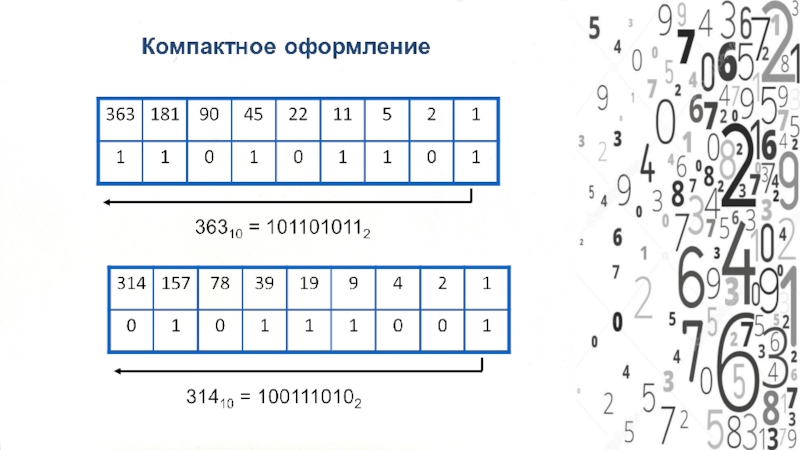
- 7. Правило перевода целых десятичных чисел в двоичную систему счисления
- 8. Двоичной системой счисления называется позиционная система счисления с основанием 2.Двоичный алфавит: 0 и 1.
- 9. Слайд 9
- 10. Слайд 10
- 11. Восьмеричная система счисленияПереведем число 101100001000110010₂ в восьмеричную
- 12. Шестнадцатеричная система счисленияПереведем число 1001011101111₂ в шестнадцатеричную
- 13. Система счисления называется непозиционной, если количественный эквивалент
- 14. Задания для самостоятельной работыДано А=A716, B=2518. Какое
- 15. Вычислите сумму чисел X и Y, если
- 16. Не ВЕРНО!!!!
- 17. Не ВЕРНО!!!!
- 18. Отлично!!!
Слайд 3Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Слайд 4Цифры 1234567890 сложились в Индии около 400 г. н. э.
Арабы стали
Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе.
Слайд 5В позиционной системе счисления с основанием q любое число может быть
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.
Слайд 6Aq =±(an–1 qn–1+ an–2 qn–2+…+ a0 q0+ a–1
Примеры:
записи чисел в развёрнутой форме:
2012=2103 +0102 +1101 +2100
0,125=110-1 +210-2 +510–3
14351,1=1104 +4103 +3102 +5101 +1100 +110–1
Слайд 8Двоичной системой счисления называется позиционная система счисления с основанием 2.
Двоичный алфавит:
Слайд 11Восьмеричная система счисления
Переведем число 101100001000110010₂ в восьмеричную систему счисления
Разбиваем число справа
Получаем восьмеричное представление исходного числа 541062₈
Слайд 12Шестнадцатеричная система счисления
Переведем число 1001011101111₂ в шестнадцатеричную систему счисления
Разбиваем число справа
0001 0010 1110 1111
1 2 E F
Получаем шестнадцатеричное представление исходного числа 12EF₁₆
Слайд 13Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в
Римская система счисления
Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:
каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
40
=
X
L
1935
=
M
C
M
X
X
X
V
Слайд 14Задания для самостоятельной работы
Дано А=A716, B=2518. Какое из чисел C, записанных
2) 101010102
3) 101010112
4) 101010002
1) 101011002
Слайд 15Вычислите сумму чисел X и Y, если X=1101112, Y=1358. Результат представьте
1) 110101002
2) 101001002
3) 100100112
4) 100101002
Верно