Презентация, доклад на тему Тема урока: Системы счисления. Перевод двоичных чисел в десятичную системы счисления. 9 класс.

Содержание

1. Тема урока: Системы счисления. Перевод двоичных чисел в десятичную системы счисления. 9 класс.
2. Двоичная система счисления
3. Известные системы счисления делятся на две группы:НепозиционныеПозиционные
4. Примером может служить римская система. Римские цифры
5. Позиционная система счисления - это система счисления,
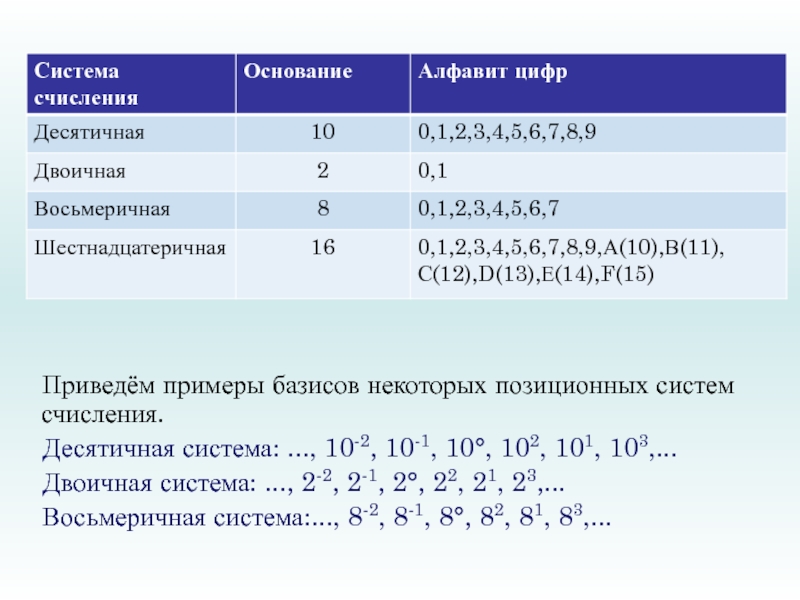
6. Приведём примеры базисов некоторых позиционных систем счисления.Десятичная
7. Пример. Разложить по базису системы счисления числа
8. Перевод двоичных чисел в десятичную системы счисления
9. Правило. Представление чисел в развернутой форме одновременно
10. Запишите в развернутом виде числа. Найдите их
11. 1)Выучить лекцию.2) Переведите исходные числа в 10-ю систему счисления:в) 1208; д) 100,112; е)10EA16. Домашняя работа

Двоичная система счисления

Главная
Информатика
Тема урока: Системы счисления. Перевод двоичных чисел в десятичную системы счисления. 9 класс.

Слайд 1Системы счисления

Слайд 2Двоичная система счисления

Слайд 3Известные системы счисления делятся на две группы:
Непозиционные
Позиционные

Слайд 4Примером может служить римская система. Римские цифры обозначаются буквами латинского алфавита:
I

V X L
5 10 50
Например:
VI = 5 +1 = 6; .
ССХС1Х = 100 + 100 + (-10 + 100) + (-1 + 10) = 299.

Непозиционная система счисления - это система счисления, в которой количественный эквивалент каждого символа не зависит от его положения (места, позиции) в записи числа.

Примером может служить римская система. Римские цифры обозначаются буквами латинского алфавита:I V X L 5 10 50Например:VI = 5 +1 =

Слайд 5Позиционная система счисления - это система счисления, в которой значение символа

(цифры) зависит от его позиции в записи числа.

Цифры - знаки, используемые при записи чисел
Алфавит - полный набор знаков системы счисления
Основание - количество используемых цифр или знаков в алфавите
Базис - включает степени основания, задающие вес разряда

385,6510= 3·102 + 8·101 + 5·100 + 6·10-1 + 5·10-2

2 1 0 -1 -2

разрядность

Основание С.с.

Базис числа

Позиционная система счисления - это система счисления, в которой значение символа (цифры) зависит от его позиции в

Слайд 6Приведём примеры базисов некоторых позиционных систем счисления.
Десятичная система: ..., 10-2, 10-1,

10°, 102, 101, 103,...
Двоичная система: ..., 2-2, 2-1, 2°, 22, 21, 23,...
Восьмеричная система:..., 8-2, 8-1, 8°, 82, 81, 83,...

Приведём примеры базисов некоторых позиционных систем счисления.Десятичная система: ..., 10-2, 10-1, 10°, 102, 101, 103,...Двоичная система: ...,

Слайд 7Пример. Разложить по базису системы счисления числа 101,012; 15FC16.

Решение
101,012 =

15FC16

=

Шестнадцатеричные цифры выражены через их десятичные значения (F = 15; С=12)

Представление чисел в развернутом виде (по базису)

Пример. Разложить по базису системы счисления числа 101,012; 15FC16.Решение 101,012 =15FC16 =Шестнадцатеричные цифры выражены через их десятичные

Слайд 8Перевод двоичных чисел в десятичную системы счисления

Слайд 9Правило. Представление чисел в развернутой форме одновременно является способом перевода чисел

в десятичную систему из двоичной системы счисления. Достаточно подсчитать результат по правилам десятичной арифметики.

1101,12 = 1 • 23 + 1 • 22 + 0 • 21 +1 • 20+1 • 2-1 =8+4+1+0,5=13,510

Перевод чисел из двоичной систем сч. десятичную
X 2⇒Y10

Правило. Представление чисел в развернутой форме одновременно является способом перевода чисел в десятичную систему из двоичной системы

Слайд 10Запишите в развернутом виде числа. Найдите их десятичный эквивалент:

а)1001,0112; б)

10111,102;
в) 11012;
2) Переведите числа в десятичную систему счисления:
а)А4516 б) 48Е16

Задание

Запишите в развернутом виде числа. Найдите их десятичный эквивалент: а)1001,0112; б) 10111,102; в) 11012; 2)

Слайд 11

1)Выучить лекцию.
2) Переведите исходные числа в 10-ю систему счисления:
в) 1208; д) 100,112;

е)10EA16.

Домашняя работа

Скачать презентацию

Презентация, доклад на тему Тема урока: Системы счисления. Перевод двоичных чисел в десятичную системы счисления. 9 класс.

Содержание

Слайд 1Системы счисления

Слайд 2Двоичная система счисления

Слайд 3Известные системы счисления делятся на две группы:
Непозиционные
Позиционные

Слайд 4Примером может служить римская система. Римские цифры обозначаются буквами латинского алфавита:
I

Слайд 5Позиционная система счисления - это система счисления, в которой значение символа

Слайд 6Приведём примеры базисов некоторых позиционных систем счисления.
Десятичная система: ..., 10-2, 10-1,

Слайд 7Пример. Разложить по базису системы счисления числа 101,012; 15FC16.

Решение
101,012 =

15FC16

Слайд 8Перевод двоичных чисел в десятичную системы счисления

Слайд 9Правило. Представление чисел в развернутой форме одновременно является способом перевода чисел

Слайд 10Запишите в развернутом виде числа. Найдите их десятичный эквивалент:

а)1001,0112; б)

Слайд 11

1)Выучить лекцию.
2) Переведите исходные числа в 10-ю систему счисления:
в) 1208; д) 100,112;

Что такое shareslide.ru?

Обратная связь

Презентация, доклад на тему Тема урока: Системы счисления. Перевод двоичных чисел в десятичную системы счисления. 9 класс.

Содержание

Слайд 1Системы счисления

Слайд 2Двоичная система счисления

Слайд 3Известные системы счисления делятся на две группы:НепозиционныеПозиционные

Слайд 4Примером может служить римская система. Римские цифры обозначаются буквами латинского алфавита:I

Слайд 5Позиционная система счисления - это система счисления, в которой значение символа

Слайд 6Приведём примеры базисов некоторых позиционных систем счисления.Десятичная система: ..., 10-2, 10-1,

Слайд 7Пример. Разложить по базису системы счисления числа 101,012; 15FC16.Решение 101,012 =15FC16

Слайд 8Перевод двоичных чисел в десятичную системы счисления

Слайд 9Правило. Представление чисел в развернутой форме одновременно является способом перевода чисел

Слайд 10Запишите в развернутом виде числа. Найдите их десятичный эквивалент: а)1001,0112; б)

Слайд 111)Выучить лекцию.2) Переведите исходные числа в 10-ю систему счисления:в) 1208; д) 100,112;

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 3Известные системы счисления делятся на две группы:
Непозиционные
Позиционные

Слайд 4Примером может служить римская система. Римские цифры обозначаются буквами латинского алфавита:
I

Слайд 6Приведём примеры базисов некоторых позиционных систем счисления.
Десятичная система: ..., 10-2, 10-1,

Слайд 7Пример. Разложить по базису системы счисления числа 101,012; 15FC16.

Решение
101,012 =

15FC16

Слайд 10Запишите в развернутом виде числа. Найдите их десятичный эквивалент:

а)1001,0112; б)

Слайд 11

1)Выучить лекцию.
2) Переведите исходные числа в 10-ю систему счисления:
в) 1208; д) 100,112;