- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Системы счисления 9 класс
Содержание
- 1. Системы счисления 9 класс
- 2. Система счисления - это знаковая система, в
- 3. Узловые числа обозначаются цифрами.Узловые и алгоритмические числаАлгоритмические
- 4. Простейшая и самая древняя система - так
- 5. Римская система счисленияНепозиционная система счисленияСистема счисления называется
- 6. Система счисления называется позиционной, если количественный эквивалент
- 7. Цифры 1234567890 сложились в Индии около 400
- 8. Двоичная система счисленияДвоичной системой счисления называется позиционная
- 9. Правило перевода целых десятичных чисел в двоичную
- 10. «Компьютерные» системы счисленияДвоичная система используется в компьютерной
Слайд 1Подготовил: учитель информатики Смирнова М.В.
СИСТЕМЫ СЧИСЛЕНИЯ
МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Слайд 2Система счисления - это знаковая система, в которой приняты определённые правила
Цифры - знаки, при помощи которых записываются числа,.
Алфавит системы счисления - совокупность цифр.
Общие сведения
Древнеславянская система счисления
Вавилонская система счисления
Египетская система счисления
Слайд 3Узловые числа обозначаются цифрами.
Узловые и алгоритмические числа
Алгоритмические числа получаются в результате
× 100 +
× 10 +
=
Слайд 4Простейшая и самая древняя система - так называемая унарная система счисления.
В ней для записи любых чисел используется всего один символ - палочка, узелок, зарубка, камушек.
Унарная система счисления
Примеры узлов «кипу»
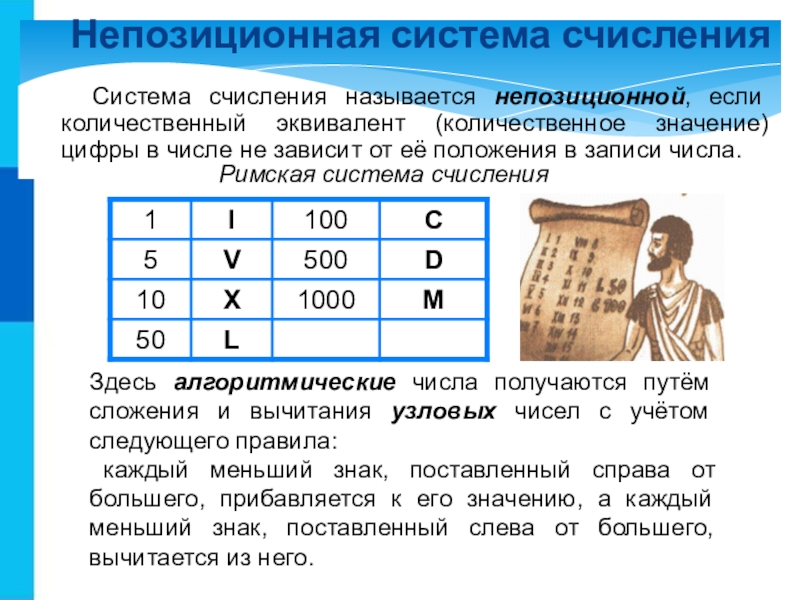
Слайд 5Римская система счисления
Непозиционная система счисления
Система счисления называется непозиционной, если количественный эквивалент
Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:
каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Слайд 6Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Позиционная система счисления
Слайд 7Цифры 1234567890 сложились в Индии около 400 г. н. э.
Арабы стали
Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе.
Десятичная система счисления
Слайд 8
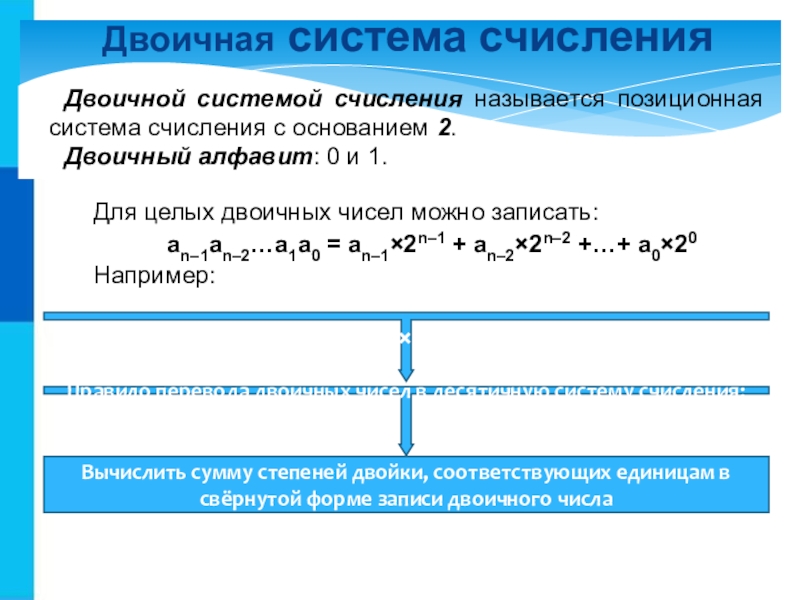
Двоичная система счисления
Двоичной системой счисления называется позиционная система счисления с основанием
Двоичный алфавит: 0 и 1.
Для целых двоичных чисел можно записать:
an–1an–2…a1a0 = an–1×2n–1 + an–2×2n–2 +…+ a0×20
Например:
100112 =1×24+0×23+0×22+1×21+1×20 = 24 +21 + 20 =1910
Правило перевода двоичных чисел в десятичную систему счисления:
Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа
Слайд 9Правило перевода целых десятичных чисел в двоичную систему счисления
an–1×2n–1+an–2×2n–2+…
= an–1×2n–2 +…+ a1 (остаток a0)
2
an–1×2n–1+an–2×2n–2+… a1
= an–1×2n–3+…+ a2 (остаток a1)
2
. . .
an–1×2n–1+an–2×2n–2+… a2
= an–1×2n–4 +…+ a3 (остаток a2)
2
На n-м шаге получим набор цифр: a0a1a2…an–1
Слайд 10«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике, так как:
двоичные числа
представление информации посредством только двух состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий логические преобразования двоичных данных.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и однородными кодами. Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.