- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Системы счисления
Содержание
- 1. Презентация по информатике на тему Системы счисления
- 2. Система счисления - это совокупность правил и приемов записи чисел с помощью набора цифровых знаков.
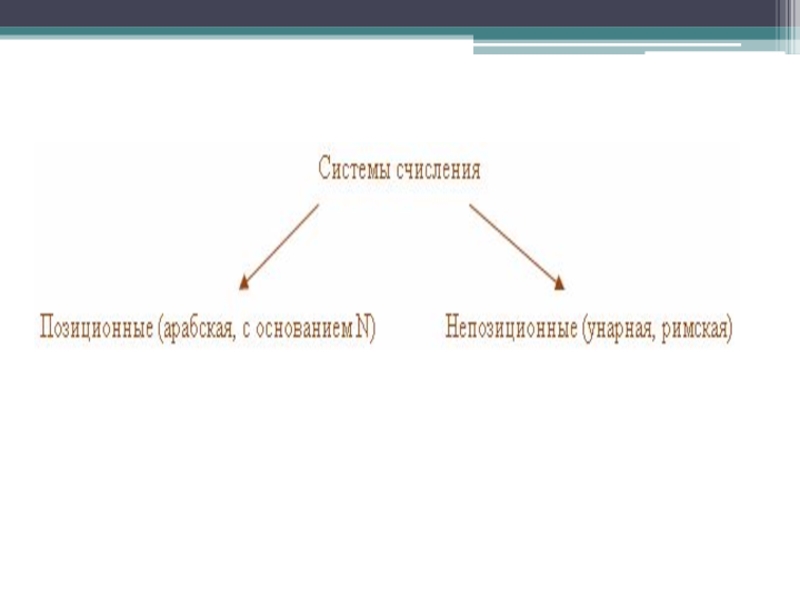
- 3. Слайд 3
- 4. Запись чисел в римской системе счисления
- 5. Алфавитом системы счисления называется совокупность всех цифр. Количество
- 6. Количество цифр, составляющих алфавит, называется его мощностью.
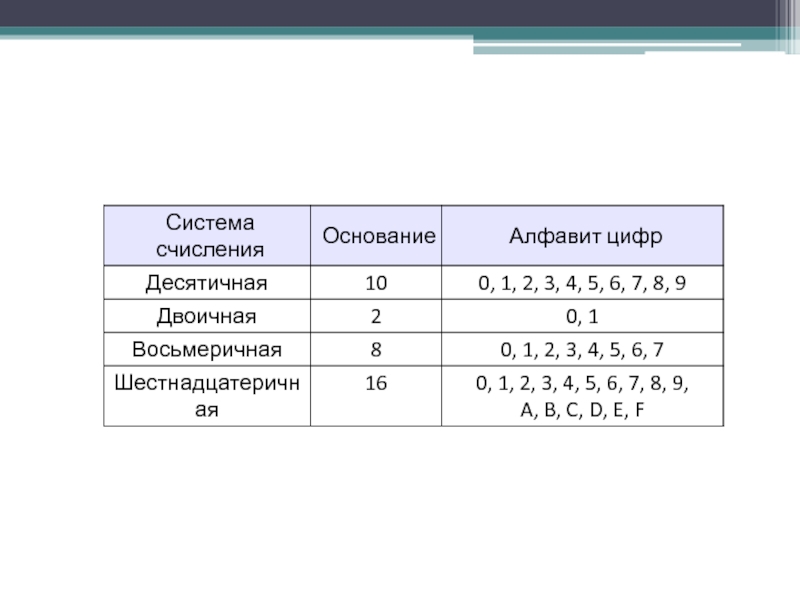
- 7. Виды систем счисления двоичная восьмеричнаядесятичная шестнадцатеричнаяДесятичная
- 8. Слайд 8
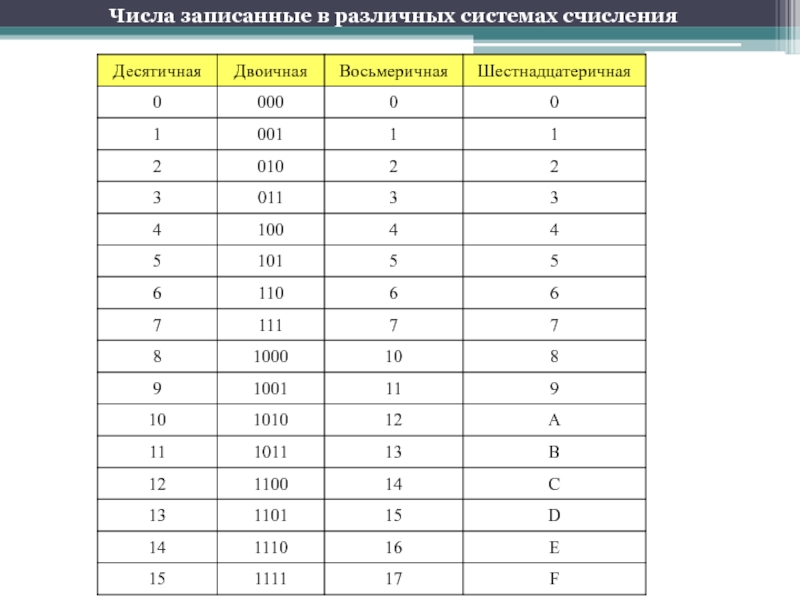
- 9. Числа записанные в различных системах счисления
- 10. Арифметические операции в позиционных с.с.
- 11. Сложение Правила сложения чисел
- 12. Пример сложения чисел 1102+ 11210012 110112+ 100121001002 11110012+ 1110102101100112
- 13. Решить примеры самостоятельно:1001100210101102
- 14. ВычитаниеПравила вычитания чисел
- 15. Если цифра в уменьшаемом меньше цифры вычитаемого,
- 16. Решить примеры самостоятельно: 100102 110102
- 17. ПРАВИЛО: Уравниваем количество разрядов в уменьшаемом и
- 18. 1000100-100011=уменьшаемоевычитаемоеразность100010001000111011100- Обратный код+11011101- Дополнительный код 1011101 10100001 Вычитание100001+
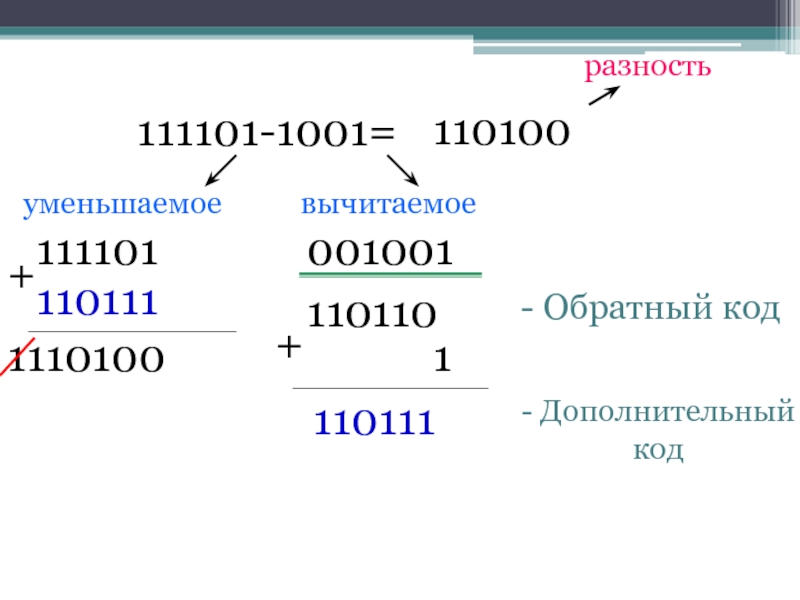
- 19. 111101-1001=уменьшаемоевычитаемоеразность111101001001110110- Обратный код+1110111- Дополнительный код1101111110100110100+
- 20. 11100102- 100012 1111110112- 101111012 11100010012- 11000011102Решить примеры самостоятельно:
- 21. Умножение0 . 0=00 . 1=01 .
- 22. Выполнить действия:1011100 +10010110011101 – 11110110101 . 1011 = 10000001= 1111111= 1001000111
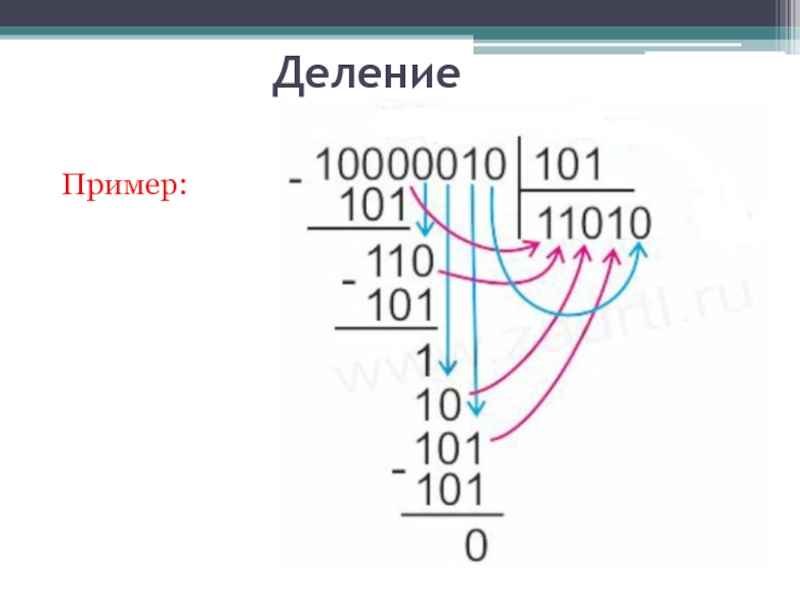
- 23. Деление110 :11=10 1 1 02- 1 1 0112102Пример:
- 24. Слайд 24
- 25. Пример: Деление
- 26. Выполнить упражнения:101111 . 11101110011101 . 1000111101111 + 111111110110 + 11101001110101111 – 1000001010001101 – 10011111011001 – 11001101101:11010011:100111100101:110010
- 27. Домашнее задание:§3.1.1.-3.1.2.Выполнить упражнения:101111 + 11101110011101 + 1000111101111 . 111111110110 – 11101001110101111 – 10000010
- 28. I вариант 1000+1000 1111+1001 1000111100+1101111 100111-11001 111000-11111 100111111-1111001 10001*10011 101011*100111 1110011*101011
- 29. Перевод из двоичной системы счисления в десятичную. 27.11.17.
- 30. Перевод из двоичной системы счисления в десятичную.Пример: 1011012= 1*25+0*24+1*23+1*22+0*21+1*20=32+0+8+4+0+1=45101100012=1*25+1*24+0*23+0*22+0*21+1*20=32+16+0+0+0+1=4910
- 31. 11000112=Х10; 2) 111011002=Х10; 3)
- 32. Перевод чисел из десятичной системы счисления в
- 33. Пример 2.12210→Х2Решение:122/2 = 61 (0 остаток)61/2 =
- 34. Задание: перевести из Х10→Х2 с.с. 5210
- 35. Домашнее заданиеПеревести из Х10→Х2 с.с. 5610 →Х2;
- 36. Перевод чисел из системы счисления с основанием
- 37. Правила перевода чисел из двоичной системы счисления
- 38. Числа записанные в различных системах счисления
- 39. Пример 1.Число 1011000010001100102 переведем в восьмеричную систему
- 40. Пример 2.Число 10000000001111100001112 переведем в шестнадцатеричную систему
- 41. Перевод дробных чиселДля того, чтобы дробное двоичное
- 42. Пример 3.Число 0,101100012 переведем в восьмеричную систему
- 43. Пример 4.Число 0,1000000000112 переведем в шестнадцатеричную систему
- 44. Перевод произвольных чиселДля того, чтобы произвольное двоичное
- 45. Пример 5.Число 111100101,01112 переведем в восьмеричную систему
- 46. Пример 6.Число 11101001000,110100102 переведем в шестнадцатеричную систему
- 47. Перевод чисел из систем счисления с основанием
- 48. Пример 7.Переведем шестнадцатеричное число 4АС3516 в двоичную систему счисления. В соответствии с алгоритмом:Получаем: 10010101100001101012.
- 49. Задание:Переведите двоичное число в восьмеричную систему счисления:
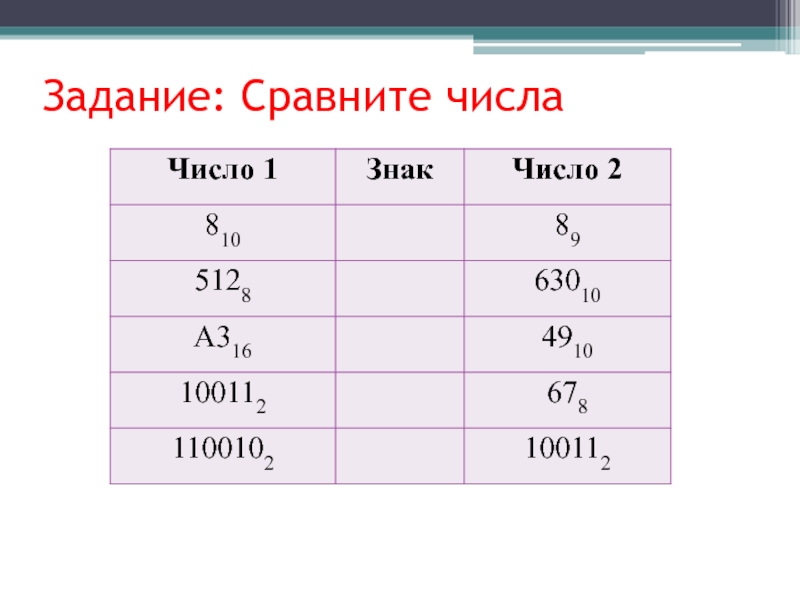
- 50. Задание: Сравните числа
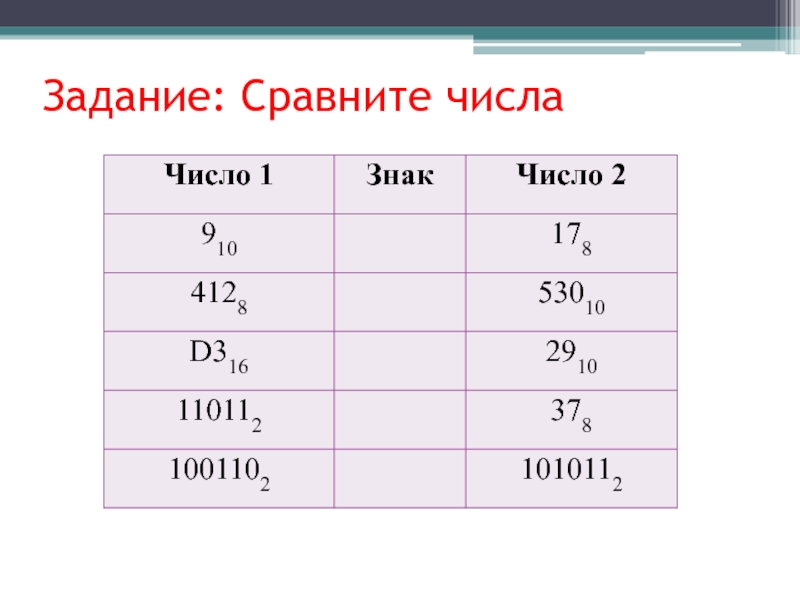
- 51. Задание: Сравните числа
- 52. Задание: 100111+10011 1100101+11100 111000-11001 10001101-110011 111111*11101
Слайд 2Система счисления - это совокупность правил и приемов записи чисел с помощью
Слайд 5Алфавитом системы счисления называется совокупность всех цифр.
Количество цифр, необходимых для записи числа
Основание системы записывается справа числа в нижнем индексе: 7810, 11000102, AF1216 и т. д.
Основание системы
Слайд 6Количество цифр, составляющих алфавит, называется его мощностью. Разряд - номер позиции в числе.
Пример.
Число 618410 запишется в форме многочлена следующим образом:
618410 = 6*103 +1*102 +8*10 1 +4*100
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания.
6184,8410 = 6*103 +1*102 +8*10 1 +4*100 +8*10 -1 +4*10-2
Слайд 7 Виды систем счисления
двоичная
восьмеричная
десятичная
шестнадцатеричная
Десятичная система использует десять цифр –
для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
В вычислительных машинах используется двоичная система счисления, её основание - число 2. Для записи чисел в этой системе используют только две цифры - 0 и 1.
Слайд 15Если цифра в уменьшаемом меньше цифры вычитаемого, то для данного вычитания
Пример
100000-11=11101
Слайд 17ПРАВИЛО:
Уравниваем количество разрядов в уменьшаемом и вычитаемом.
Находим дополнительный код к
Все 0 заменяем на 1, а 1 на 0 получим обратный код;
Прибавляем 1 в нулевом разряде обратного кода и получим дополнительный код;
Складываем уменьшаемое и дополнительный код.
Отбрасываем единицу в старшем разряде.
Слайд 181000100-100011=
уменьшаемое
вычитаемое
разность
1000100
0100011
1011100
- Обратный код
+
1
1011101
- Дополнительный код
1011101
10100001
Вычитание
100001
+
Слайд 19111101-1001=
уменьшаемое
вычитаемое
разность
111101
001001
110110
- Обратный код
+
1
110111
- Дополнительный код
110111
1110100
110100
+
Слайд 20 11100102
- 100012
1111110112
- 101111012
11100010012
- 11000011102
Решить
Слайд 22Выполнить действия:
1011100 +100101
10011101 – 11110
110101 . 1011
= 10000001
= 1111111
= 1001000111
Слайд 26Выполнить упражнения:
101111 . 11101
110011101 . 1000111
101111 + 1111
11110110 + 1110100
1110101111 –
10001101 – 100111
11011001 – 1100110
1101:110
10011:1001
11100101:110010
Слайд 27Домашнее задание:
§3.1.1.-3.1.2.
Выполнить упражнения:
101111 + 11101
110011101 + 1000111
101111 . 1111
11110110 – 1110100
1110101111
Слайд 28I вариант
1000+1000
1111+1001
1000111100+1101111
100111-11001
111000-11111
100111111-1111001
10001*10011
101011*100111
1110011*101011
Слайд 30Перевод из двоичной системы счисления в десятичную.
Пример:
1011012= 1*25+0*24+1*23+1*22+0*21+1*20=32+0+8+4+0+1=4510
1100012=1*25+1*24+0*23+0*22+0*21+1*20=32+16+0+0+0+1=4910
Слайд 3111000112=Х10; 2) 111011002=Х10;
3) 10010012=Х10; 4)
5)1100001112=Х10; 6)11010112=Х10;
7) 1000110012=Х10 ; 8) 110011112=Х10;
9) 1011100112=Х10 ; 10) 111111112 =Х10.
Задание: перевести из Х2 →Х10 с.с.
Слайд 32Перевод чисел из десятичной системы счисления в двоичную.
Пример 1.
7710→Х2
Решение:
77
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении.
Проверка:
10011012 =1*26 + 0*25 + 0*24 +1*23 + 1*22 + 0*21 + 1*20=64 + 0+0+8 + 4 + 0 + 1 = 7710.
7710→ 10011012
Слайд 33Пример 2.
12210→Х2
Решение:
122/2 = 61 (0 остаток)
61/2 = 30 (1 остаток)
30/2
15/2 = 7 (1остаток)
7/2 = 3 (1 остаток)
3/2 = 1 (1 остаток)
1/2 = 0 (1 остаток)
Проверка:
11110102=1*26+1*25+1*24+1*23+0*22+1*21+0*20=64+32+16+8+0+2+0=12210
Перевод чисел из десятичной системы счисления в двоичную.
Слайд 34Задание: перевести из Х10→Х2 с.с.
5210 = Х2; 2) 6510
5) 11610 = Х2; 6) 13210 = Х2; 7) 14410 = Х2; 8) 15610 = Х2;
9) 19910 = Х2; 10) 23410 = Х2; 11) 25010 = Х2.
Слайд 35Домашнее задание
Перевести из Х10→Х2 с.с.
5610 →Х2; 7810 →Х2; 8910 →Х2.
Перевести из Х2→Х10 с.с.
1001102 →Х10; 111001102 →Х10; 1010100112 →Х10.
Слайд 36Перевод чисел из системы счисления с основанием 2 в систему счисления
18.10.17.
Слайд 37Правила перевода чисел из двоичной системы счисления в n-ичную и обратно
1. Двоичное
2. Если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n.
Слайд 39Пример 1.
Число 1011000010001100102 переведем в восьмеричную систему счисления.
Разбиваем число справа налево
Получаем восьмеричное представление исходного числа: 5410628.
Слайд 40Пример 2.
Число 10000000001111100001112 переведем в шестнадцатеричную систему счисления.
Получаем шестнадцатеричное представление исходного числа: 200F8716.
Слайд 41Перевод дробных чисел
Для того, чтобы дробное двоичное число записать в системе
1. Двоичное число разбить слева направо на группы по n цифр в каждой.
2. Если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n.
Слайд 42Пример 3.
Число 0,101100012 переведем в восьмеричную систему счисления.
Получаем восьмеричное представление исходного числа: 0,5428.
Слайд 43Пример 4.
Число 0,1000000000112 переведем в шестнадцатеричную систему счисления.
Разбиваем число слева направо на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 0,80316.
Слайд 44Перевод произвольных чисел
Для того, чтобы произвольное двоичное число записать в системе
1. Целую часть данного двоичного числа разбить справа налево, а дробную — слева направо на группы по n цифр в каждой.
2. Если в последних левой и/или правой группах окажется меньше n разрядов, то их надо дополнить слева и/или справа нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n .
Слайд 45Пример 5.
Число 111100101,01112 переведем в восьмеричную систему счисления.
Получаем восьмеричное представление исходного числа: 745,348.
Слайд 46Пример 6.
Число 11101001000,110100102 переведем в шестнадцатеричную систему счисления.
Разбиваем целую
Получаем шестнадцатеричное представление исходного числа: 748,D216.
Слайд 47Перевод чисел из систем счисления с основанием q=2n в двоичную систему
Для
Слайд 48Пример 7.
Переведем шестнадцатеричное число 4АС3516 в двоичную систему счисления. В соответствии
Получаем: 10010101100001101012.
Слайд 49Задание:
Переведите двоичное число в восьмеричную систему счисления:
1) 1100111; 2) 110011100;
Переведите двоичное число в шестнадцатеричную счисления:
1) 1100111; 2) 110011100; 3) 10010011001100
Переведите дробное двоичное число в восьмеричную систему счисления:
1) 0,11010111; 2) 0,100011100; 3) 1,10010011001100
Переведите дробное двоичное число в шестнадцатеричную систему счисления:
1) 0,11010111; 2) 0,100011100; 3) 1,10010011001100;
Переведите произвольное двоичное число в восьмеричную систему счисления:
1) 1100,11010111; 2) 11110,100011100; 3) 10011,10010011001100;
Переведите произвольное двоичное число в шестнадцатеричную систему счисления:
1) 1100,11010111; 2) 11110,100011100; 3) 10011,10010011001100;
Переведите шестнадцатеричное число в двоичную систему счисления:
1) 5СА4; 2) А23ВС; 3) 18Е4F1D3