- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Системы счисления
Содержание
- 1. Системы счисления
- 2. «И в небе и на земле сокрыто
- 3. Содержание презентацииЧто можно назвать системой счисления?Как изображали
- 4. Что можно назвать системой счисления?Система счисления- это
- 5. Числа изображали засечками на деревянных дощечках; клиньями
- 6. Арифметические операции в любых системах счисления базируются
- 7. Какими бывают системы счисления?Системы счисления бывают непозиционные
- 8. Системы счисления позиционные непозиционные Количественные значения символов,
- 9. Как считать в непозиционной системе?Имеются знаки для узловых чисел:
- 10. Как записываются числа в римской
- 11. Почему непозиционные системы используются редко?Непозиционные
- 12. Принципы организации любой позиционной системы счисления?-величина, обозначаемая
- 13. Каким может быть основание
- 14. Почему люди пользуются десятичной системы счисления?«Преимущество десятичной
- 15. Как указать принадлежность числа к какой-либо системе
- 16. КАК ПЕРЕВЕСТИ ЧИСЛО В ДЕСЯТИЧНУЮ СИСТЕМУ СЧИСЛЕНИЙ?Например,
- 17. Мы привыкли считать и записывать числа в
- 18. Как перевести десятичные числа в другие системы
- 19. Римская система счисления
- 20. Система счисления в Древнем Египте
- 21. Система счисления египтянИероглифическая система счисления имеет основание
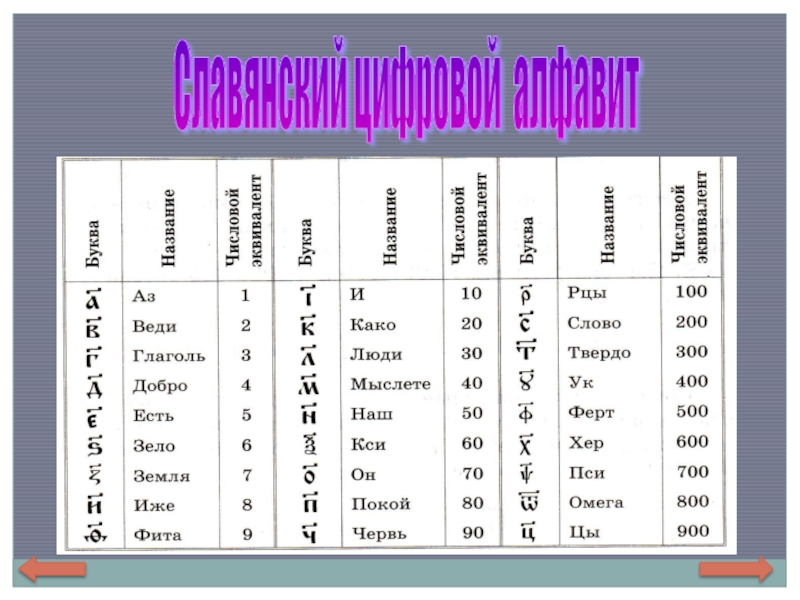
- 22. Алфавитные системы счисления
- 23. Славянский цифровой алфавит
- 24. Глиняные таблички, найденные в Месопатамии с культурным
- 25. Система счисления вавилонян (на основе позиционного принципа)Дополнительные сведения
- 26. Всё КОНЕЦ!!!
Слайд 2«И в небе и на земле сокрыто больше,
Чем снится вашей
Шекспир
____________ ________ __________
Слайд 3Содержание презентации
Что можно назвать системой счисления?
Как изображали числа?
Что лежит в основе
Какими бывают системы счисления?
Как считать в непозиционной системе?
Как записываются числа в римской нумерации?
Почему непозиционные системы используются редко?
Принципы организации любой позиционной системы счисления?
Каким может быть основание позиционной системы счисления?
Почему люди пользуются десятичной системой счисления?
Как указать принадлежность числа к какой-либо системе счисления?
Как перевести число в десятичную систему счисления?
Как перевести десятичные числа в другие системы счисления?
Какие в древности использовались системы счисления?
Слайд 4Что можно назвать системой счисления?
Система счисления- это способ изображения чисел и
Слайд 5Числа изображали засечками на деревянных дощечках; клиньями на глиняных табличках; узелками
Как изображали числа?
Слайд 6Арифметические операции в любых системах счисления базируются на таблицах сложения и
Что лежит в основе правил арифметики любой системы счисления?
Слайд 7Какими бывают системы счисления?
Системы счисления бывают непозиционные и позиционные. В непозиционных
Например , в десятичной системе счисления записано число 333:
- 3 справа обозначает три и единицы;
- 3 в середине обозначает три десятка;
- 3 слева обозначает три сотни.
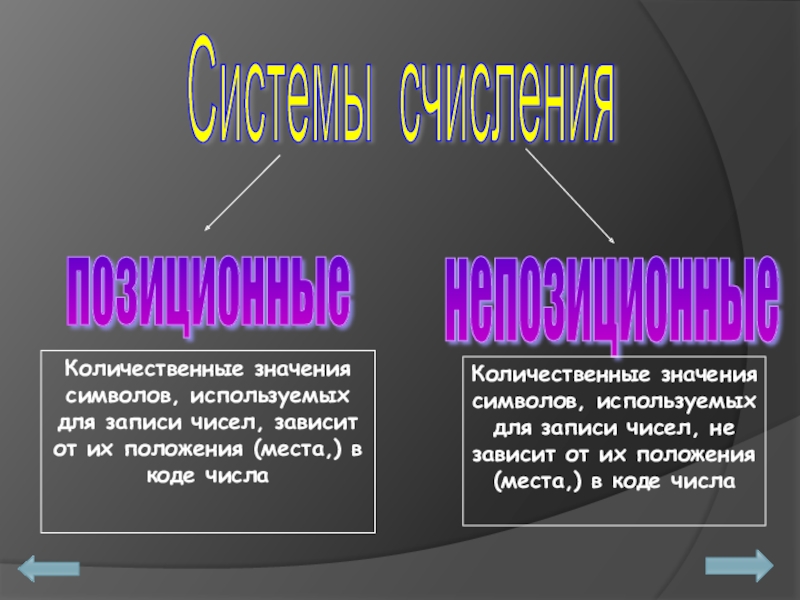
Слайд 8Системы счисления
позиционные
непозиционные
Количественные значения символов, используемых для записи чисел,
Количественные значения символов, используемых для записи чисел, зависит от их положения (места,) в коде числа
Слайд 10
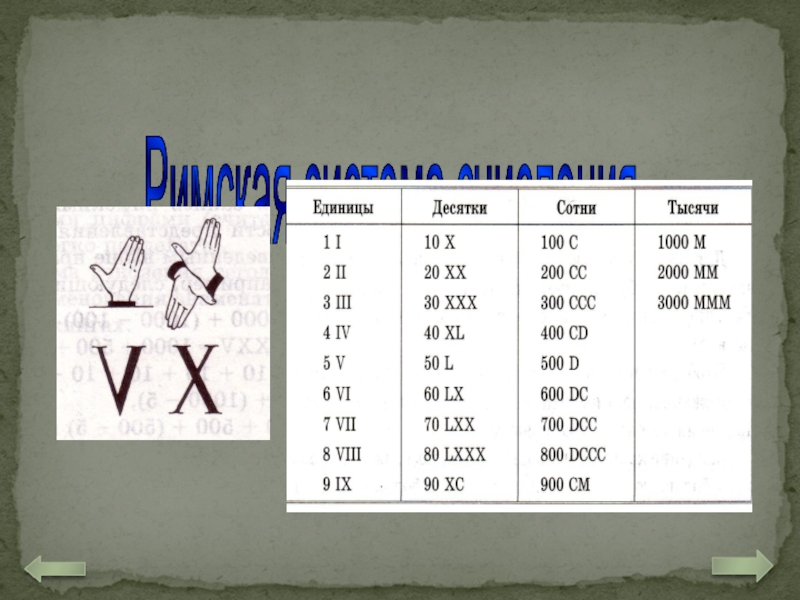
Как записываются числа в римской нумерации?
Цифры записываются слева направо в порядке
Их значение складывается. Если слева записана меньшая цифра, а справа большая, то их значения вычитаются.
Например:
CCХХl l-двести тридцать два, Vl – представимо как 5+1=6,
lV- представимо как 5-1=4
MCMХCVlll =1000+( -10+ 100) +5+1+1+1=1998.
Слайд 11
Почему непозиционные системы используются редко?
Непозиционные системы удобнее, чем зарубки на
Слайд 12Принципы организации любой позиционной системы счисления?
-величина, обозначаемая цифрой в записи числа,
- выбрано основание системы – количество цифр, используемых в системе.
Слайд 13Каким может быть основание
Основанием позиционной системы счисления может быть любое натуральное число, большее 1 В системе с основанием n нужно иметь алфавит из n цифр.
Слайд 14Почему люди пользуются десятичной системы счисления?
«Преимущество десятичной системы не математическое,
Слайд 15Как указать принадлежность числа к какой-либо системе счисления?
Основание системы приписывается нижним
1123 = 1410
Слайд 16КАК ПЕРЕВЕСТИ ЧИСЛО В ДЕСЯТИЧНУЮ СИСТЕМУ СЧИСЛЕНИЙ?
Например, число 112, записанное в
Слайд 17Мы привыкли считать и записывать числа
в десятичной системе счисления.
Но
Слайд 18Как перевести десятичные числа в другие системы
счисления?
Заданное десятичное число делится
Слайд 21Система счисления египтян
Иероглифическая система счисления имеет основание 10 и не является
Дополнительные сведения
Слайд 24Глиняные таблички, найденные в Месопатамии с культурным центром - г.Вавилон.
Около
Вавилонская система счисления :
является комбинацией шестидесятеричной и десятичной систем с применением позиционного принципа;
используется всего два символа для обозначения числа 1 и числа10 .
шестидесятеричной системой пользуются до сих пор при измерении времени и углов.