Презентация, доклад на тему Решение задач ЕГЭ по теме Системы счисления

записанных в двоичной системе, отвечает условию N1) 100110012 2) 100111002 3) 100001102 4) 100110002

Е
Г
Э

Решение:
Переводим числа в одну систему счисления, например в восьмеричную 9916=1001 10012 =10 011 0012=2318
Переводим ответы в восьмеричную систему счисления
10 011 0012=2318 10 011 1002=2348
10 000 1102=2068
10 011 0002=2308

среди этих чисел то, в двоичной записи которого содержится ровно 5 единиц. Если таких чисел несколько, укажите наибольшее из них.
1) 1510 2) 778 3) 3458 4) FA16

Решение:
Для решения задачи необходимо перевести в двоичную систему счисления все числа.
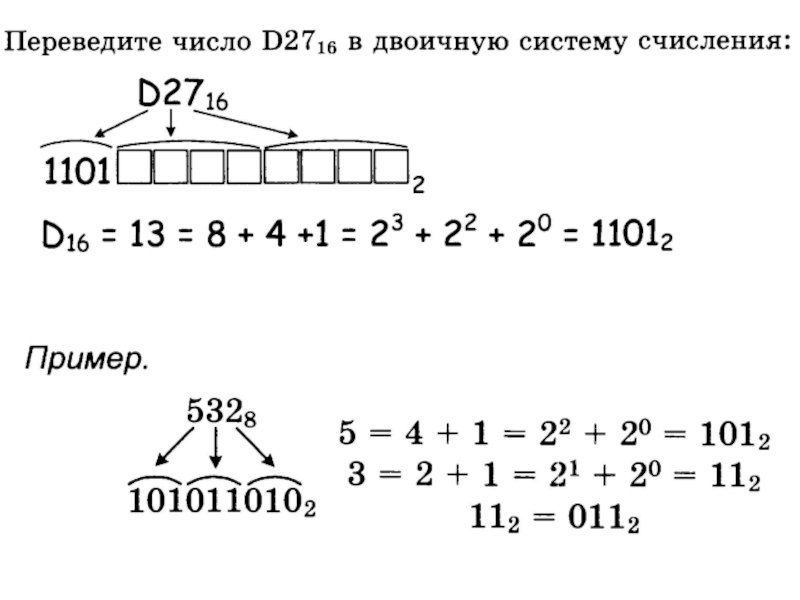
Первое число переводим любым методом, поскольку оно небольшое. Например, разложим его на сумму степеней двойки:
15 = 8 + 4 +2 + 1 =23 + 22 +21 + 20 = 11112
 Три следующих числа переводим, используя таблицы соответствия двоичной-восьмиричной и двоичной-шестнадцатиричной (таблицы соответствия систем счисления, родственных двоичной).
 778 = 111 1112
3458 = 11 100 1012
FA16 = 1111 10102
 Как видим, два числа имеют в двоичной системе счисления 5 единиц – число 1510 = 11112 и число 3458 = 11 100 1012. В нашем случае в ответе требуется указать наибольшее из них – это число 3458
Ответ: 3)

счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 4 единицы. Если таких чисел несколько, укажите наибольшее из них.
1) 1410 2) 3418 3) 718 4) F716
Ответ: 2)
Задание 7
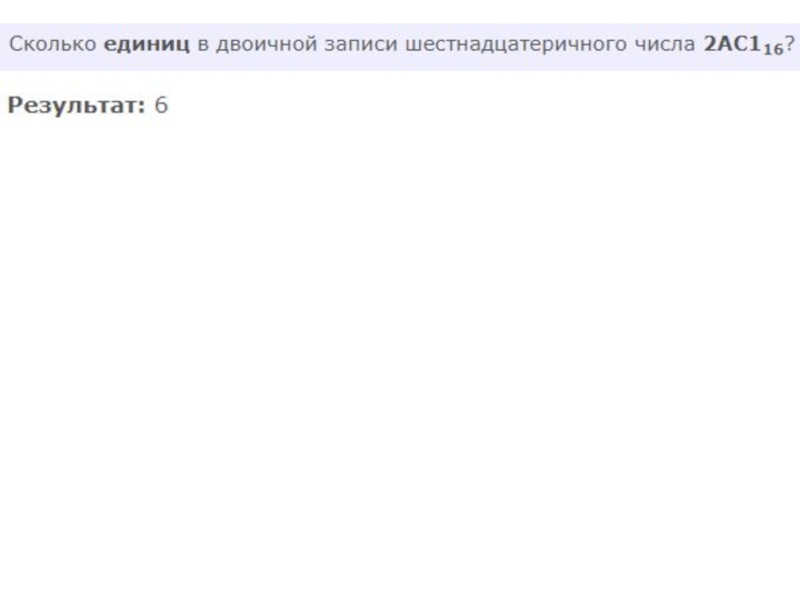
Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 6 единиц. Если таких чисел несколько, укажите наибольшее из них.
1) FA16 2) 2510 3) 3458 4) 778
Ответ: 1)
Задание 8
Даны 4 числа, они записаны с использованием разных систем счисления. Укажите среди них то число, двоичная запись которого содержит ровно шесть «1». Если таких чисел несколько, укажите наибольшее из них.
1)6310*410 2)3338 3)F816 + 110 4)111001112
Ответ: 1)

230. Определите основание системы счисления.

Решение
По условию задачи: 65 = 230р, где р – искомое основание системы счисления.
Представим это равенство в десятичной системе счисления: 65 = 2*р2 + 3*р
Получаем квадратное уравнение 2р2 + 3р - 65 = 0
Находим его корни, учитывая, что основание системы счисления р – натуральное число (p>=2).
Получаем р=5.
Ответ: 5

записывается как 101. Укажите это основание.
Ответ: 5
 
Задание 18
В системе счисления с некоторым основанием десятичное число 27 записывается как 1000. Укажите это основание.
Ответ: 3
 
Задание 19
В системе счисления с некоторым основанием десятичное число 37записывается как 101. Укажите это основание.
Ответ: 6
 
Задание 20
В системе счисления с некоторым основанием десятичное число 37 записывается как 123. Укажите это основание.
Ответ: 5

дайте в троичной системе счисления.
Решение
1) Переведём все числа в десятичную систему счисления:
121х = 1·х2 + 2·х + 1 1017 = 1·72 + 0·71 +1·70=50
2) Собираем всё в одно уравнение, получаем х2 + 2х + 1 +1 + 50 х2 + 2х – 48 = 0
Это уравнение имеет два решения, х=6 и х= -8; основание системы счисления – натуральное число, поэтому ответ х= 6
3)Переводим ответ в троичную систему: 6 = 2∙31 = 203.
Ответ: 203

в шестиричной системе счисления. Основание системы счисления не указывать.
Ответ: 153
 Задание 24
Решите уравнение 123 + 12x = 128
Ответ: 3
 Задание 25
Решите уравнение 1007 + x = 2305
Ответ: 16
 Задание 26
Решите уравнение 215 + 113 = 120x
Ответ: 3

равенство 147 + x = 14y. Ответ запишите в троичной системе счисления через запятую. Основание системы счисления указывать не нужно.
Решение:
1)запишем равенство в десятичной системе счисления:
1*7 + 4 + х = y + 4 11 + x = y + 4
2) Из условия следует, что y>=5 (т.к. число 14y в системе счисления с основанием у содержит значащие цифры 1 и 4). Минимальное значение уmin = 5.
3) Минимальное значение хmin получается при минимальном значении уmin .
4) При уmin=5 получаем хmin=2 .
5) Переводим 2 и 5 в троичную систему счисления: 2 =23 5=123.
Ответ: 2,12

Для какого двоичного числа с выполняется неравенство a1) 10010011 2) 10001110 3) 10001010 4) 10001100
Решение: необходимо все числа перевести в одну и ту же систему счисления.
(через десятичную систему счисления):
а=9*16+2=146 b=2*64+2*8+4=148
1) 147 2) 142 3) 138 4) 135
Находим значение с, лежащее в интервале от а до b.
Ответ: 1)
Решать задачу через переводы чисел в восьмиричную или шестнадцатиричную системы счисления – нерационально, хотя для любителей оных – пожалуйста!

778. Для какого двоичного числа с выполняется неравенство a1) 111101 2) 111110 3) 111111 4) 111010
Ответ: 2)
 Задание 34 – (ФИПИ)
Даны числа а = 5D16 и b = 1378. Для какого двоичного числа с выполняется неравенство a1) 1011110 2) 1001101 3) 100111 4) 1011100
Ответ: 1)
 Задание 35
Даны числа а = 8B16 и b = 2158. Для какого двоичного числа с выполняется неравенство a1) 10010011 2) 10001100 3) 10001010 4) 10001100
Ответ: 2)