Ерина
Руководитель работы Кормилицына Т. В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задач арифметики в пакетах символьной математики.
Содержание
- 1. Решение задач арифметики в пакетах символьной математики.
- 2. Одним из факторов, определяющих уровень развития современного
- 3. МapleАналитическое решение дифференциальных уравненийОбщее решение дифференциальных уравнений.Для
- 4. Команда dsolve выдает решение дифференциального уравнения в не вычисляемом
- 5. Слайд 5
- 6. Слайд 6
- 7. MathcadАналитические вычисления в MathcadС помощью аналитических вычислений
- 8. Слайд 8
- 9. Команды для выполнения аналитических вычислений в основном
- 10. В меню Символика (Symbolics) предусмотрен ряд операций, ориентированных на
- 11. Другие возможности использования этого меню включают:аналитическое дифференцирование
- 12. замена переменной: Символика > Переменная > Подставить (Symbolics >
- 13. Механизм аналитических вычислений можно использовать для аналитического
- 14. Отметим, что функция Find пытается найти решение в аналитической
- 15. MATLABРешение систем дифференциальных уравнений в символьном виде
- 16. Пример решения задачиОбратите внимание, что уравнение, которое
- 17. С помощью команды solve можно решать высокоуровневые
- 18. Математические пакеты Maple и MATLAB — интеллектуальные
- 19. Слайд 19
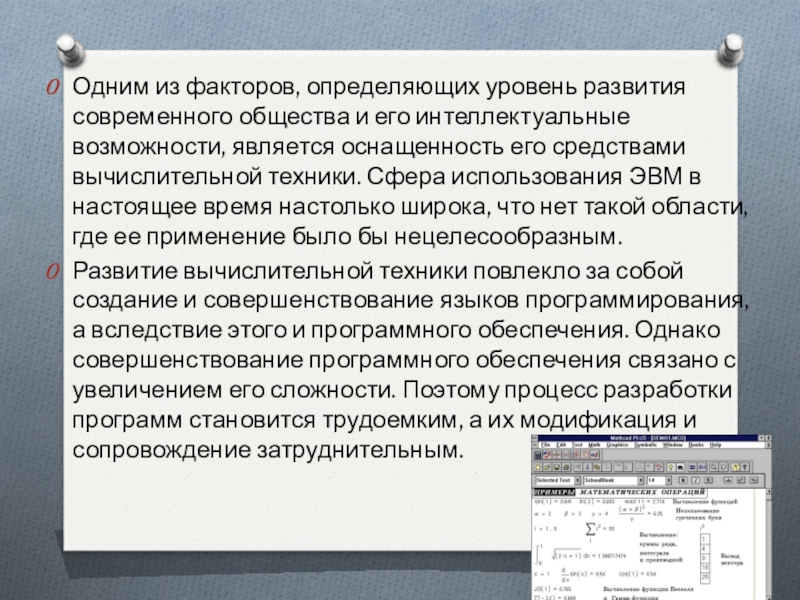
Одним из факторов, определяющих уровень развития современного общества и его интеллектуальные возможности, является оснащенность его средствами вычислительной техники. Сфера использования ЭВМ в настоящее время настолько широка, что нет такой области, где ее применение было бы нецелесообразным.Развитие
Слайд 2Одним из факторов, определяющих уровень развития современного общества и его интеллектуальные
возможности, является оснащенность его средствами вычислительной техники. Сфера использования ЭВМ в настоящее время настолько широка, что нет такой области, где ее применение было бы нецелесообразным.
Развитие вычислительной техники повлекло за собой создание и совершенствование языков программирования, а вследствие этого и программного обеспечения. Однако совершенствование программного обеспечения связано с увеличением его сложности. Поэтому процесс разработки программ становится трудоемким, а их модификация и сопровождение затруднительным.
Развитие вычислительной техники повлекло за собой создание и совершенствование языков программирования, а вследствие этого и программного обеспечения. Однако совершенствование программного обеспечения связано с увеличением его сложности. Поэтому процесс разработки программ становится трудоемким, а их модификация и сопровождение затруднительным.
Слайд 3Мaple
Аналитическое решение дифференциальных уравнений
Общее решение дифференциальных уравнений.
Для нахождения аналитических решений дифференциальных
уравнений в Maple применяется команда dsolve(eq,var,options),где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact. При составлении дифференциальных уравнений для обозначения производной применяется команда diff, например, дифференциальное уравнение y''+y=xзаписывается в виде: diff(y(x),x$2)+y(x)=x.
Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _С1, _С2, и т.д
Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _С1, _С2, и т.д
Слайд 4Команда dsolve выдает решение дифференциального уравнения в не вычисляемом формате. Для того, чтобы
с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командой rhs(%).
Слайд 7Mathcad
Аналитические вычисления в Mathcad
С помощью аналитических вычислений находят аналитические или полные
решения уравнений и систем, вычисляют в производные и неопределенные интегралы, а также проводят преобразования сложных выражений (например, упрощение). Иначе говоря, при таком подходе можно получить результат в виде некоторой функции. В программе Mathcad при проведении символьных преобразований конкретные значения, присвоенные переменным, игнорируются – переменные рассматриваются как неопределенные параметры.
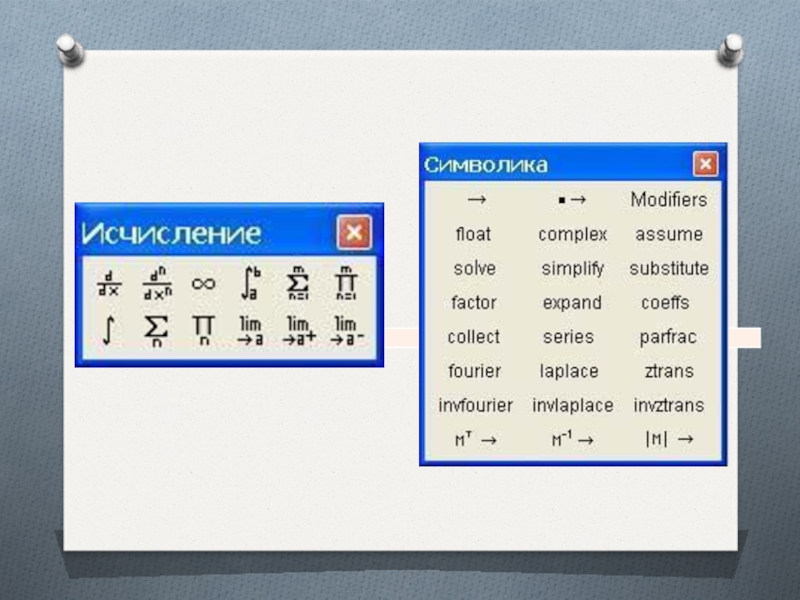
Слайд 9Команды для выполнения аналитических вычислений в основном сосредоточены в меню Символика (Symbolics) и
продублированы на аналогичной панели инструментов.
Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Символика > Упростить (Symbolics > Simplify). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тождества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции. Некоторые действия по раскрытию скобок и упрощению сложных тригонометрических выражений требуют применения команды Символика > Раскрыть/Расширить (Symbolics > Expand).
Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Символика > Упростить (Symbolics > Simplify). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тождества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции. Некоторые действия по раскрытию скобок и упрощению сложных тригонометрических выражений требуют применения команды Символика > Раскрыть/Расширить (Symbolics > Expand).
Слайд 10В меню Символика (Symbolics) предусмотрен ряд операций, ориентированных на выделенную переменную, использованную в
выражении. Например, команда Solve (Решить) ищет корни функции, заданной данным выражением. В примере в аналитической форме получены все корни полинома второй степени: сначала применена команда solve для решения, а затем simplify для упрощения результата:
Слайд 11Другие возможности использования этого меню включают:
аналитическое дифференцирование и интегрирование: Символика > Переменная
> Дифференцировать (Symbolics > Variable > Differentiate) и Символика > Переменная > Интегрировать (Symbolics > Variable > Integrate);
Слайд 12замена переменной: Символика > Переменная > Подставить (Symbolics > Variable > Substitute) –
вместо переменной подставляется содержимое буфера обмена;
Слайд 13Механизм аналитических вычислений можно использовать для аналитического решения уравнений и систем
уравнений и неравенств. Для этого задается блок решения Given, в который помещаются уравния и неравенства, а последняя формула блока должна выглядеть как
Find(х,у,...) ,
где в скобках приведен список искомых величин, а далее следует знак аналитического вычисления, отображаемый в виде стрелки, направленной вправо:
Find(х,у,...) ,
где в скобках приведен список искомых величин, а далее следует знак аналитического вычисления, отображаемый в виде стрелки, направленной вправо:
Слайд 14Отметим, что функция Find пытается найти решение в аналитической форме. В том случае,
если до блока Given задать численно значения всех параметров, входящих в уравнения, а также начальные приближения для корней, то получим решение в числовом виде.
Примеры использования функции Find для решения уравнений и систем уравнений различного типа приведены в соответствующих разделах пособия.
Любое аналитическое вычисление можно применить с помощью ключевого слова.
Примеры использования функции Find для решения уравнений и систем уравнений различного типа приведены в соответствующих разделах пособия.
Любое аналитическое вычисление можно применить с помощью ключевого слова.
Слайд 15MATLAB
Решение систем дифференциальных уравнений в символьном виде в системе MATLAB
Для решения
дифференциальных уравнений в форме Коши MatLAB имеет функцию dsolve(‘eqn1’,’eqn2’, …), которая возвращает аналитическое решение системы дифференциальных уравнений с начальными условиями. Они задаются равенствами eqni(вначале задаются уравнения, затем начальные условия).
По умолчанию независимой переменной считается ‘t’ . Можно использовать и другую переменную, включив ее в конец списка параметров функции dsolve. Символ D обозначает производную по независимой переменной, то есть d/dt, при этом D2 означает d^2/dt^2 и т.д.
Начальные условия задаются в виде равенств ‘y(a) = b’ или ‘Dy(a) = b’, где y - независимая переменная, a и b – константы. Если число начальных условий меньше, чем число дифференциальных уравнений, то в решений будут присутствовать произвольные постоянные С1, С2 и т.д. Вывод осуществляется в виде массива записей.
По умолчанию независимой переменной считается ‘t’ . Можно использовать и другую переменную, включив ее в конец списка параметров функции dsolve. Символ D обозначает производную по независимой переменной, то есть d/dt, при этом D2 означает d^2/dt^2 и т.д.
Начальные условия задаются в виде равенств ‘y(a) = b’ или ‘Dy(a) = b’, где y - независимая переменная, a и b – константы. Если число начальных условий меньше, чем число дифференциальных уравнений, то в решений будут присутствовать произвольные постоянные С1, С2 и т.д. Вывод осуществляется в виде массива записей.
Слайд 16Пример решения задачи
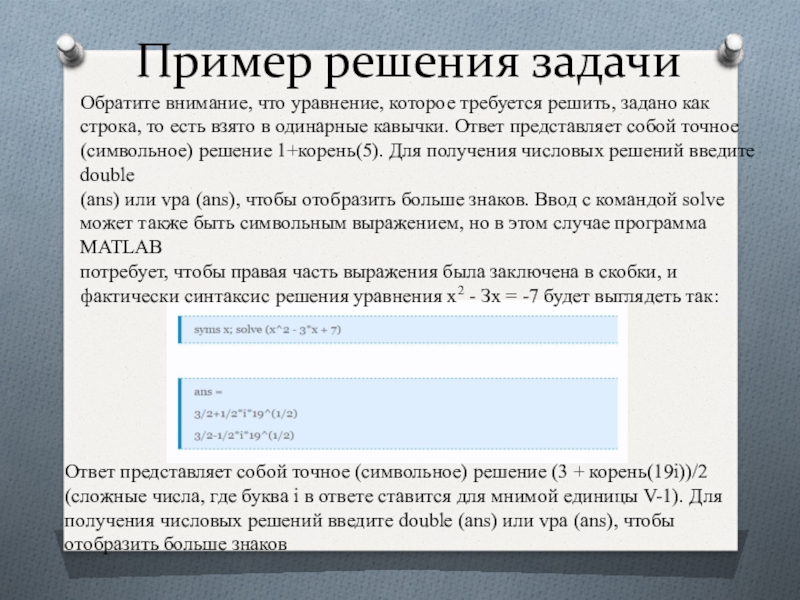
Обратите внимание, что уравнение, которое требуется решить, задано как
строка, то есть взято в одинарные кавычки. Ответ представляет собой точное
(символьное) решение 1+корень(5). Для получения числовых решений введите double
(ans) или vpa (ans), чтобы отобразить больше знаков. Ввод с командой solve
может также быть символьным выражением, но в этом случае программа MATLAB
потребует, чтобы правая часть выражения была заключена в скобки, и
фактически синтаксис решения уравнения х2 - Зх = -7 будет выглядеть так:
Ответ представляет собой точное (символьное) решение (3 + корень(19i))/2
(сложные числа, где буква i в ответе ставится для мнимой единицы V-1). Для
получения числовых решений введите double (ans) или vpa (ans), чтобы
отобразить больше знаков
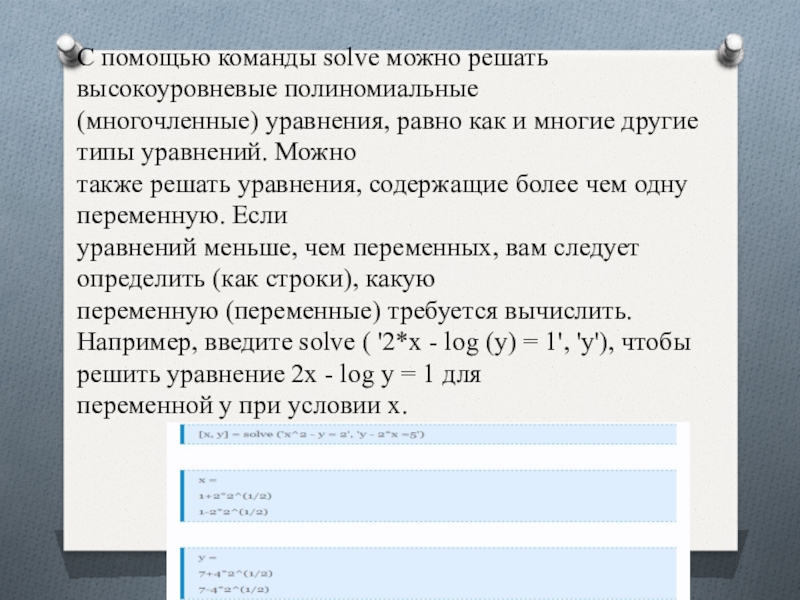
Слайд 17С помощью команды solve можно решать высокоуровневые полиномиальные (многочленные) уравнения, равно как
и многие другие типы уравнений. Можно
также решать уравнения, содержащие более чем одну переменную. Если
уравнений меньше, чем переменных, вам следует определить (как строки), какую
переменную (переменные) требуется вычислить. Например, введите solve ( '2*х - log (у) = 1', 'у'), чтобы решить уравнение 2х - log у = 1 для
переменной у при условии х.
Слайд 18Математические пакеты Maple и MATLAB — интеллектуальные лидеры в своих классах
и образцы, определяющие развитие компьютерной математики. Компьютерная алгебра Maple вошла составной частью в ряд современных пакетов, численный анализ от MATLAB и наборы инструментов (Toolboxes) уникальны. Сами пакеты постоянно совершенствуются, развивая аппарат и пополняя ресурсы. Пакет Maple и вычислительная среда MATLAB — мощные и хорошо организованные системы, надежные и простые в работе. Освоение даже части их возможностей даст несомненный эффект, а по мере накопления опыта придет настоящая эффективность от взаимодействия с ними.[9]