- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение систем логических уравнений
Содержание
- 1. Решение систем логических уравнений
- 2. Системы логических уравнений (ЕГЭ-2011)Три типа задач:I тип
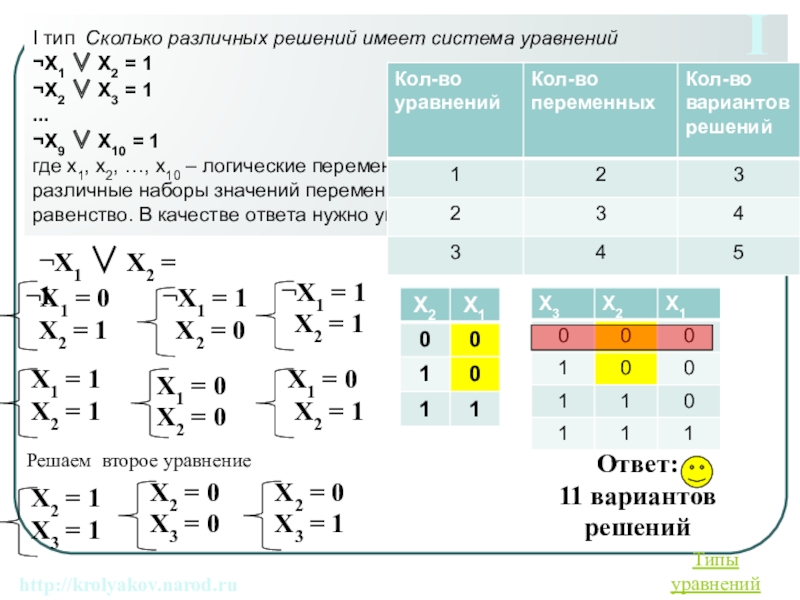
- 3. I тип Сколько различных решений имеет система
- 4. Сколько различных решений имеет система уравнений X1
- 5. Сколько различных решений имеет система уравнений ¬X1
- 6. Вывод:Система уравнений типа ¬X1 X2 =
- 7. Задача 1.Следующие два высказывания истинны:Неверно, что если
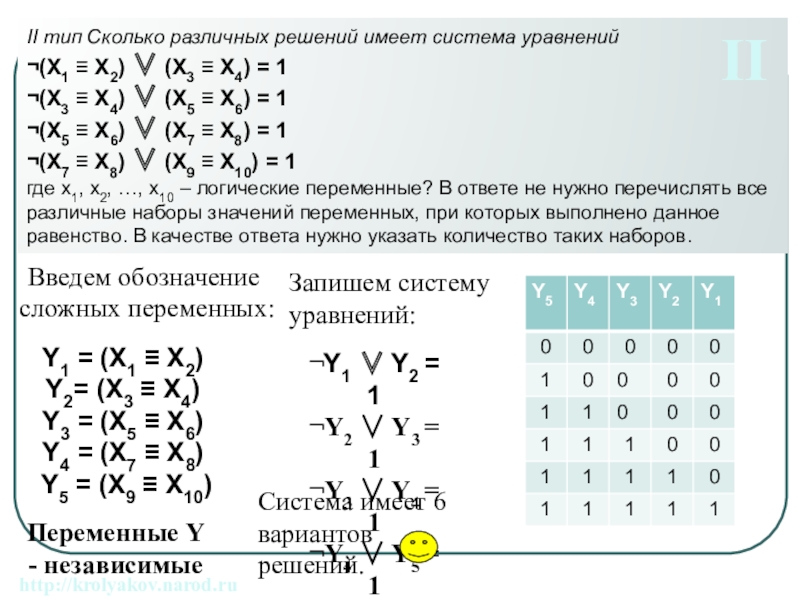
- 8. II тип Сколько различных решений имеет система
- 9. Найдем варианты решений для исходных переменныхКол-во комбинаций
- 10. III. Сколько различных решений имеет система уравнений
- 11. Замена эквивалентностиЗакон замены эквивалентности:A B =
- 12. Введем обозначение сложных переменных: Y1 = (X1
- 13. Сколько различных решений имеет система уравнений ((X1
- 14. Введем обозначение сложных переменных: Y1 = (X1
- 15. Сколько различных решений имеет система уравнений (X2
- 16. V(X2 X1) (X2 X3)
- 17. V(X10 X1) = 0X10 X1Подключаем последнее уравнение:Ответ: Кол-во решений = 20-2=18http://krolyakov.narod.ru
- 18. VI. Сколько различных решений имеет система уравнений
- 19. Решаем первое уравнение:(X1 X2)(X1 X3)=1Решаем второе уравнение:(X2 X3)(X2 X4)=1VIhttp://krolyakov.narod.ru
- 20. Ответ: 20 вариантовVIhttp://krolyakov.narod.ru
- 21. (X1 X2)(X1 X3)=1(X2 X3)(X2
- 22. VIIСколько различных решений имеет система уравнений (X1
- 23. VII
- 24. Сколько различных решений имеет система уравнений ((X1
- 25. Сколько различных решений имеет система уравнений (X1
- 26. Решаем первое уравнение:(X1 X2) (X1
- 27. Решаем предпоследнее и последнее уравнения:(X3 X4)
- 28. Решаем первое уравнение:(X1 X2) (X1
- 29. Сколько различных решений имеет система уравнений ((X1
- 30. Cистема имеет 2 варианта решения.В152012 гУпростим уравнения:¬(Y1
Слайд 2Системы логических уравнений
(ЕГЭ-2011)
Три типа задач:
I тип - В уравнениях используется операции
II тип - В уравнениях используется операции дизъюнкции (конъюнкции), сложные переменные представлены тождеством, одна сложная переменная входит в 2 уравнения.
III тип - В уравнениях используется операции дизъюнкции (конъюнкции), сложные переменные, которые могут быть упрощены путем введения независимых новых переменных и применения законов логических преобразований.
IV тип - В уравнениях используется операции дизъюнкции (конъюнкции), сложные переменные, которые не могут быть упрощены путем введения независимых новых переменных.
V тип – Одна переменная входит в одно слагаемое во всех уравнениях
VI, VII тип – Одна переменная входит во все слагаемые в уравнении
Слайд 3I тип Сколько различных решений имеет система уравнений
¬X1 X2 =
¬X2 X3 = 1
...
¬X9 X10 = 1
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
¬X1 X2 = 1
Ответ:
11 вариантов решений
Типы уравнений
I
Решаем второе уравнение
http://krolyakov.narod.ru
Слайд 4Сколько различных решений имеет система уравнений
X1 ¬ X2 =
X2 ¬ X3 = 1
...
X9 ¬ X10 = 1
где x1, x2, …, x10 – логические переменные?
Решаем самостоятельно
Первое уравнение: X1 ¬ X2 = 1
Второе уравнение: X2 ¬ X3 = 1
Ответ:
11 вариантов решений
http://krolyakov.narod.ru
Слайд 5Сколько различных решений имеет система уравнений
¬X1 X2 = 0
¬X2
...
¬X9 X10 = 0
где x1, x2, …, x10 – логические переменные?
Сколько различных решений имеет система уравнений
¬X1 X2 = 0
¬X2 X3 = 0
...
¬X9 X10 = 0
где x1, x2, …, x10 – логические переменные?
Сколько различных решений имеет система уравнений
¬X1 X2 = 1
¬X2 X3 = 1
...
¬X9 X10 = 1
где x1, x2, …, x10 – логические переменные?
Нет решения
I
11 вариантов
Нет решения
Слайд 6Вывод:
Система уравнений типа ¬X1 X2 = 1, где
используются операции дизъюнкции
Кол-во вариантов решений = кол-во уравнений + 2, или
Кол-во вариантов решений = кол-во переменных + 1.
I
Слайд 7Задача 1.
Следующие два высказывания истинны:
Неверно, что если корабль А вышел в
В море вышел корабль В или корабль С, но не оба вместе. Какие корабли вышли в море.
А= «корабль А вышел в море»
В= «корабль В вышел в море»
С= «корабль С вышел в море»
А→ ¬ С = 0
А В = 1
Последовательное решение уравнений:
А В = 1
А = 1
В = 0
А = 0
В = 1
А→ ¬ С = 0
А = 1
¬ С = 0
А = 1
С = 1
А = 1
В = 0
С=1
Ответ:
Слайд 8II тип Сколько различных решений имеет система уравнений
¬(X1 X2)
¬(X3 X4) (X5 X6) = 1
¬(X5 X6) (X7 X8) = 1
¬(X7 X8) (X9 X10) = 1
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Введем обозначение
сложных переменных:
Y1 = (X1 X2)
Y2= (X3 X4)
Y3 = (X5 X6)
Y4 = (X7 X8)
Y5 = (X9 X10)
Запишем систему уравнений:
¬Y1 Y2 = 1
¬Y2 Y3 = 1
¬Y3 Y4 = 1
¬Y4 Y5 = 1
Cистема имеет 6 вариантов решений.
Переменные Y - независимые
II
http://krolyakov.narod.ru
Слайд 9Найдем варианты решений для исходных переменных
Кол-во комбинаций для одного варианта решений:
Всего решений: 32*6=192
Алгоритм
1. Ввести обозначения для сложных переменных.
2. Записать систему для новых переменных.
3. Найти количество вариантов решений для системы с новыми переменными (m).
4. Определить число состояний (k) исходных переменных для одного варианта решения.
5. Определить число комбинаций (N) с учетом всего количества введенных переменных (n): N=kn
6. Определить итоговое количество вариантов решения системы:
N*m
II
http://krolyakov.narod.ru
Слайд 10III. Сколько различных решений имеет система уравнений
(X1 X2)
(X3 X4) (¬X3 ¬X4) (¬X5 X6) (X5 ¬X6) = 1
(X5 X6) (¬X5 ¬X6) (¬X7 X8) (X7 ¬X8) = 1
(X7 X8) (¬X7 ¬X8) (¬X9 X10) (X9 ¬X10) = 1
где x1, x2, …, x10 – логические переменные?
Используется закон замены эквивалентности:
A B = (A B) (¬ A ¬B)
и замены инверсии эквивалентности:
¬ (A B) = ¬((A B) (¬ A ¬B)) = ¬(A B) ¬(¬ A ¬B) =
(¬ A ¬ B) (A B) = ¬ A A ¬ A B A ¬ B ¬ B B =
(¬ A B) (A ¬ B )
III
(X1 X2) ¬ (X3 X4) =1
(X3 X4) ¬ (X5 X6) =1
(X5 X6) ¬ (X7 X8) =1
(X7 X8) ¬ (X9 X10) =1
Упростим уравнения:
Решить самостоятельно. Проверка
http://krolyakov.narod.ru
Слайд 11Замена эквивалентности
Закон замены эквивалентности:
A B = (A B)
Замена инверсии эквивалентности:
¬ (A B) = ¬((A B) (¬ A ¬B)) = ¬(A B) ¬(¬ A ¬B) =
(¬ A ¬ B) (A B) = ¬ A A ¬ A B A ¬ B ¬ B B =
(¬ A B) (A ¬ B )
Слайд 12Введем обозначение
сложных переменных:
Y1 = (X1 X2)
Y2= (X3
Y3 = (X5 X6)
Y4 = (X7 X8)
Y5 = (X9 X10)
Запишем систему уравнений:
Y1 ¬Y2 = 1
Y2 ¬Y3 = 1
Y3 ¬Y4 = 1
Y4 ¬Y5 = 1
Cистема имеет 6 вариантов решений.
III
Найдем варианты решений для исходных переменных
N=25=32
Всего решений:
32*6=192
http://krolyakov.narod.ru
Слайд 13Сколько различных решений имеет система уравнений
((X1 X2) (X3
((X3 X4) (X5 X6)) (¬(X3 X4) ¬(X5 X6)) = 1
((X5 X6) (X7 X8)) (¬(X5 X6) ¬(X7 X8)) = 1
((X7 X8) (X9 X10)) (¬(X7 X8) ¬(X9 X10)) = 1
где x1, x2, …, x10 – логические переменные?
IV
Алгоритм решения:
Вводим обозначения сложных высказываний и переписываем уравнения.
Упрощаем уравнения, используя замену эквивалентности и инверсии эквивалентности.
Определяем количество вариантов решения для веденных переменных.
Определяем количество комбинаций исходных переменных для одного варианта.
Определяем итоговое количество вариантов решения
Решаем самостоятельно
http://krolyakov.narod.ru
Слайд 14Введем обозначение
сложных переменных:
Y1 = (X1 X2)
Y2= (X3
Y3 = (X5 X6)
Y4 = (X7 X8)
Y5 = (X9 X10)
Запишем систему уравнений:
(Y1 Y2) (¬ Y1 ¬ Y2) = 1
(Y2 Y3) (¬ Y2 ¬ Y3) = 1
(Y3 Y4) (¬ Y3 ¬ Y4) = 1
(Y4 Y5) (¬ Y4 ¬ Y5) = 1
Cистема имеет 2 варианта решения.
IV
Упростим уравнения:
Y1 Y2 = 1
Y2 Y3 = 1
Y3 Y4 = 1
Y4 Y5 = 1
Кол-во комбинаций для одного варианта решений: N=25=32
Всего решений: 32*2=64
http://krolyakov.narod.ru
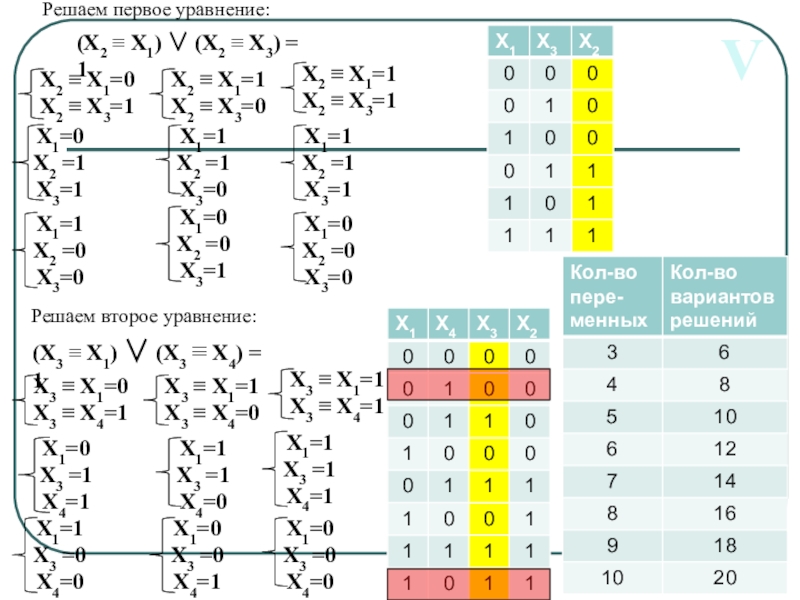
Слайд 15Сколько различных решений имеет система уравнений
(X2 X1) (X2
(X3 X1) (X3 X4) (¬X3 ¬ X4)= 1
...
(X9 X1) (X9 X10) (¬X9 ¬ X10)= 1
(X10 X1) = 0
где x1, x2, …, x10 – логические переменные?
V
Используется закон замены эквивалентности:
(X2 X1) (X2 X3) = 1
(X3 X1) (X3 X4) = 1
...
(X9 X1) (X9 X10)= 1
(X10 X1) = 0
http://krolyakov.narod.ru
Слайд 16V
(X2 X1) (X2 X3) = 1
Решаем второе уравнение:
(X3
Решаем первое уравнение:
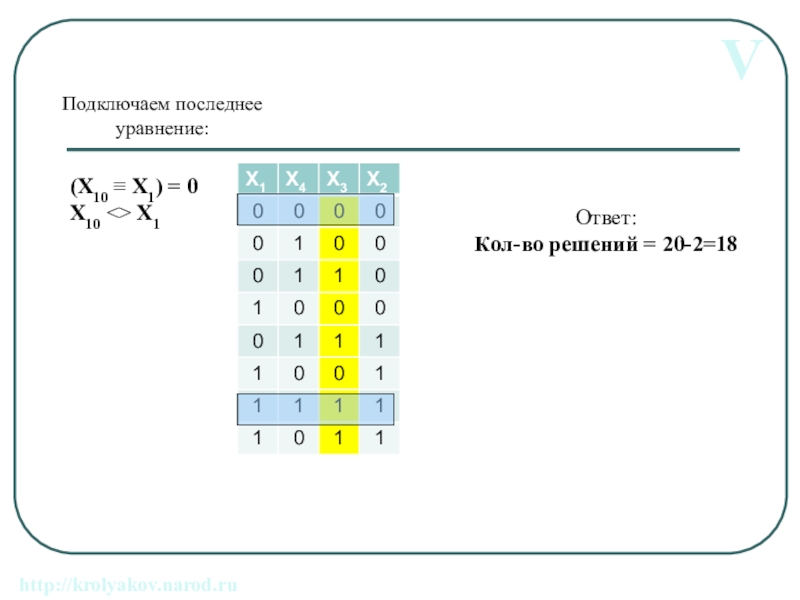
Слайд 17V
(X10 X1) = 0
X10 X1
Подключаем последнее уравнение:
Ответ:
Кол-во решений
http://krolyakov.narod.ru
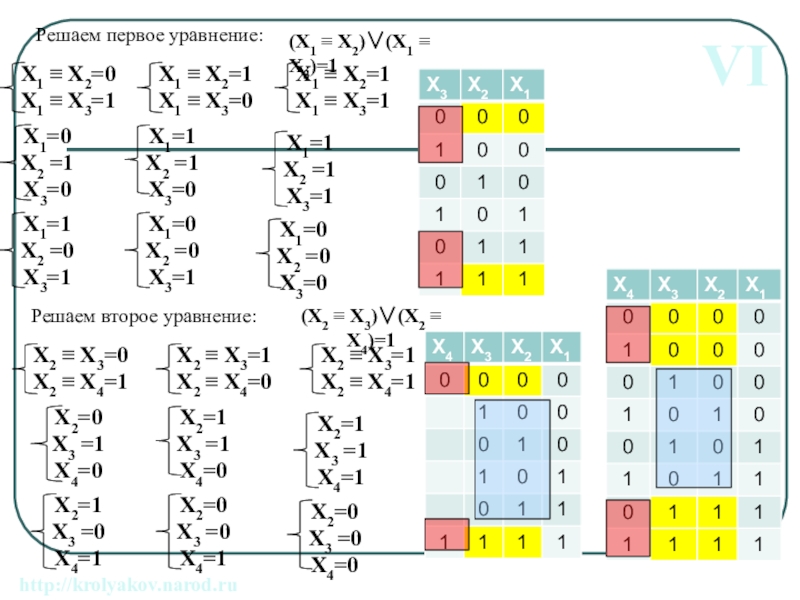
Слайд 18VI. Сколько различных решений имеет система уравнений
(X1 X2)
(X2 X3) (¬X2 ¬X3) (X2 X4) = 1
...
(X8 X9) (¬X8 ¬X9) (X8 X10) = 1
где x1, x2, …, x10 – логические переменные?
VI
Решаем самостоятельно
Применим закон замены эквивалентности:
(X1 X2)(X1 X3)=1
(X2 X3)(X2 X4)=1
...
(X8 X9)(X8 X10)=1
http://krolyakov.narod.ru
Слайд 19Решаем первое уравнение:
(X1 X2)(X1 X3)=1
Решаем второе уравнение:
(X2 X3)(X2
VI
http://krolyakov.narod.ru
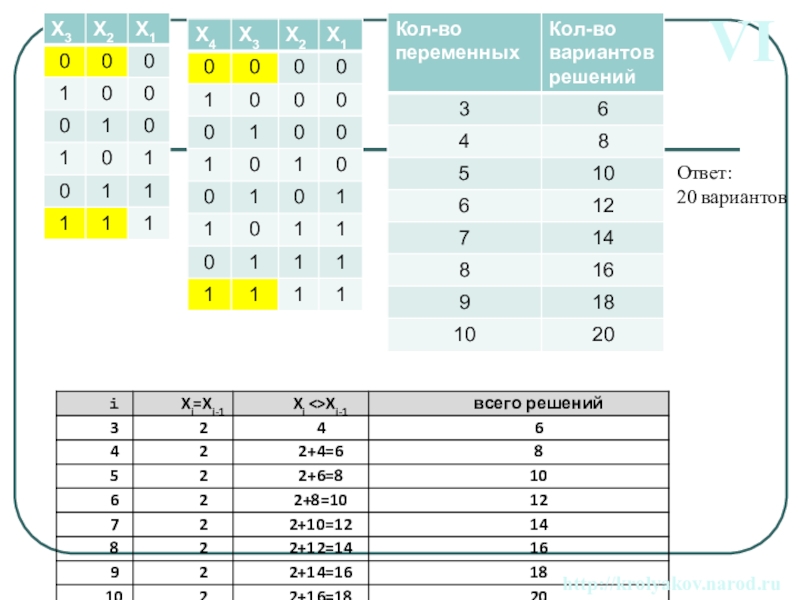
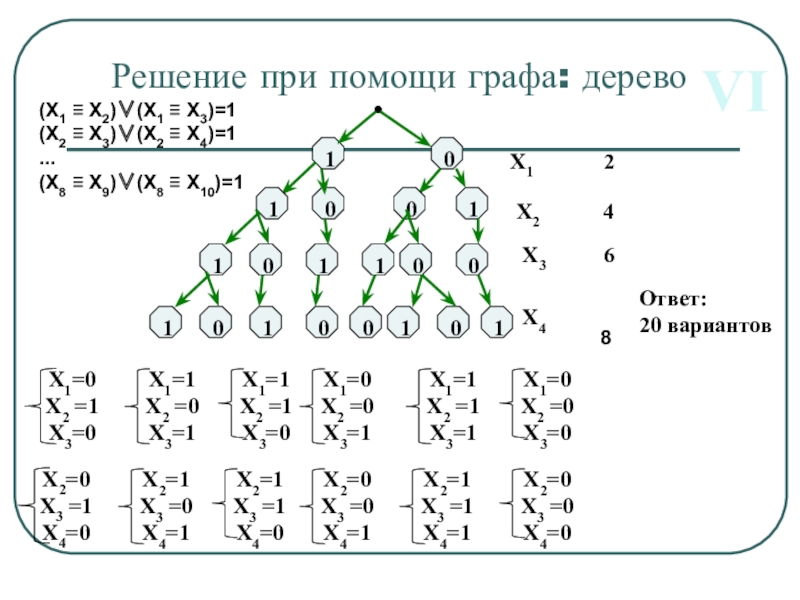
Слайд 21(X1 X2)(X1 X3)=1
(X2 X3)(X2 X4)=1
...
(X8 X9)(X8
Решение при помощи графа: дерево
1
0
X1
X2
1
X3
1
0
0
1
1
0
1
0
0
2
4
6
1
0
X4
1
0
0
1
0
1
8
Ответ:
20 вариантов
VI
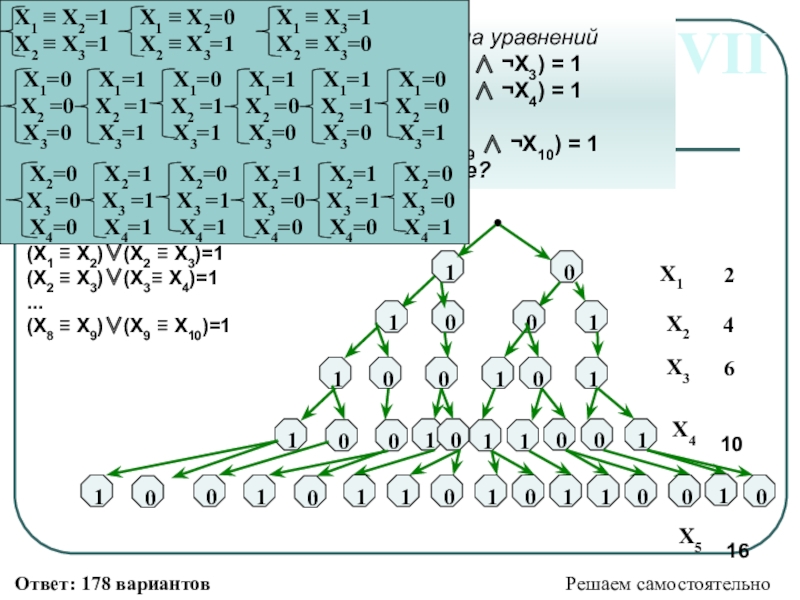
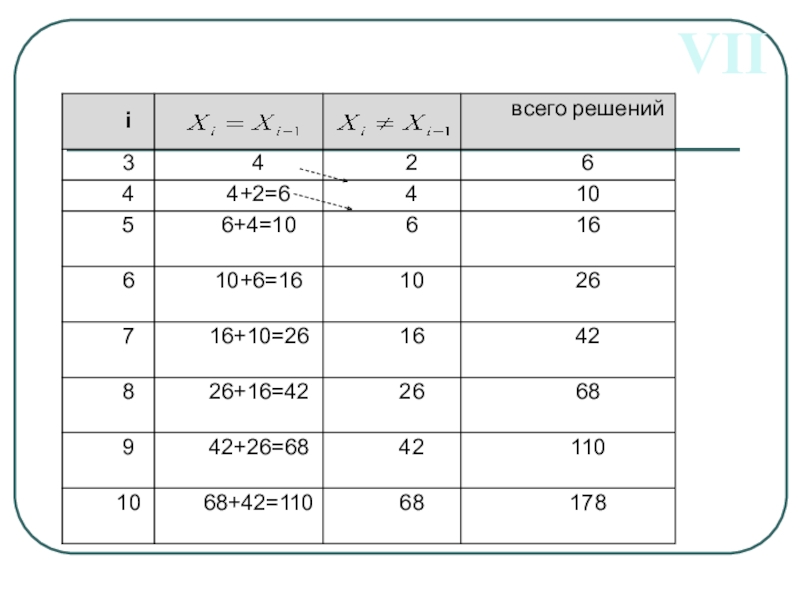
Слайд 22VII
Сколько различных решений имеет система уравнений
(X1 X2) (¬X1
(X2 X3) (¬X2 ¬X3) (X3 X4) (¬X3 ¬X4) = 1
...
(X8 X9) (¬X8 ¬X9) (X9 X10) (¬X9 ¬X10) = 1
где x1, x2, …, x10 – логические переменные?
Применим закон замены эквивалентности:
(X1 X2)(X2 X3)=1
(X2 X3)(X3 X4)=1
...
(X8 X9)(X9 X10)=1
Решаем самостоятельно
Ответ: 178 вариантов
1
0
X1
X2
1
X3
1
0
0
0
1
0
1
0
1
2
4
6
1
0
X4
0
0
1
1
0
1
10
1
0
0
1
0
0
1
1
0
1
0
1
1
0
1
0
0
1
X5
16
Слайд 24Сколько различных решений имеет система уравнений
((X1 X2) (X3
((X3 X4) (X5 X6)) (¬(X3 X4) ¬(X5 X6)) = 0
((X5 X6) (X7 X8)) (¬(X5 X6) ¬(X7 X8)) = 0
((X7 X8) (X9 X10)) (¬(X7 X8) ¬(X9 X10)) = 0
где x1, x2, …, x10 – логические переменные?
http://krolyakov.narod.ru для самостоятельного решения № 52
Получается 2 варианта решения.
Каждая переменная Y имеет две пары значений (0, 1), т. е. число комбинаций исходных переменных в одном варианте равно 25=32.
Кол-во вариантов решений = 32*2=64
X1 X2 =Y1
X3 X4 =Y2
X5 X6 =Y3
X7 X8 =Y4
X9 X10 =Y5
Перепишем систему:
(Y1 Y2 ) (¬ Y1 ¬Y2) = 0
(Y2 Y3 ) (¬ Y2 ¬Y3) = 0
(Y3 Y4 ) (¬ Y3 ¬Y4) = 0
(Y4 Y5 ) (¬ Y4 ¬Y5) = 0
Применим закон замены эквивалентности:
Y1 Y2 = 0
Y2 Y3 = 0
Y3Y4 = 0
Y4 Y5 = 0
Введем
обозначения:
VIII
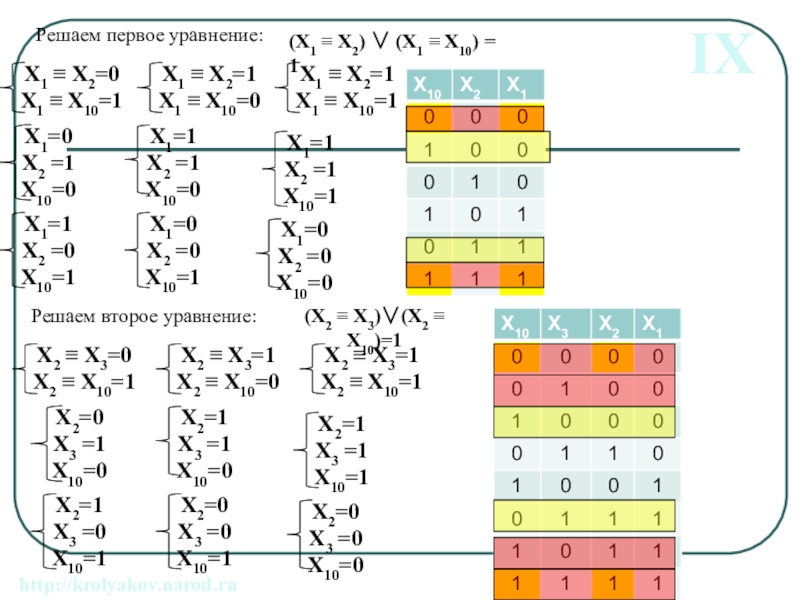
Слайд 25Сколько различных решений имеет система уравнений
(X1 X2) (X1
(X2 X3) (X2 X10) (¬X2 ¬ X10)= 1
...
(X9 X10) (X9 X10) (¬X9 ¬ X10)= 1
(X1 X10) = 0
где x1, x2, …, x10 – логические переменные?
http://krolyakov.narod.ru для самостоятельного решения № 55
Применим закон замены эквивалентности:
(X1 X2) (X1 X10) = 1
(X2 X3) (X2 X10)= 1
...
(X9 X10) = 1
(X1 X10) = 0
IX
Слайд 26Решаем первое уравнение:
(X1 X2) (X1 X10) = 1
Решаем
(X2 X3)(X2 X10)=1
http://krolyakov.narod.ru
IX
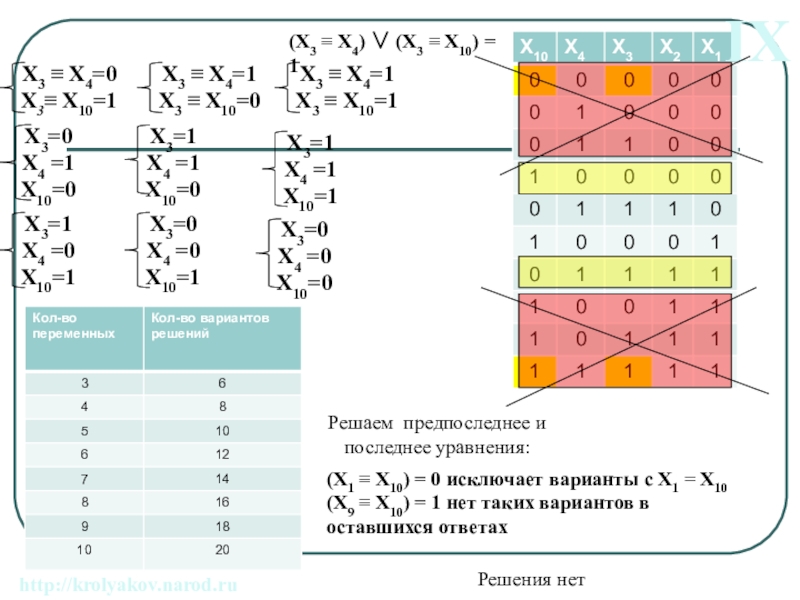
Слайд 27Решаем предпоследнее и последнее уравнения:
(X3 X4) (X3 X10)
IX
http://krolyakov.narod.ru
(X1 X10) = 0 исключает варианты с X1 = X10
(X9 X10) = 1 нет таких вариантов в оставшихся ответах
Решения нет
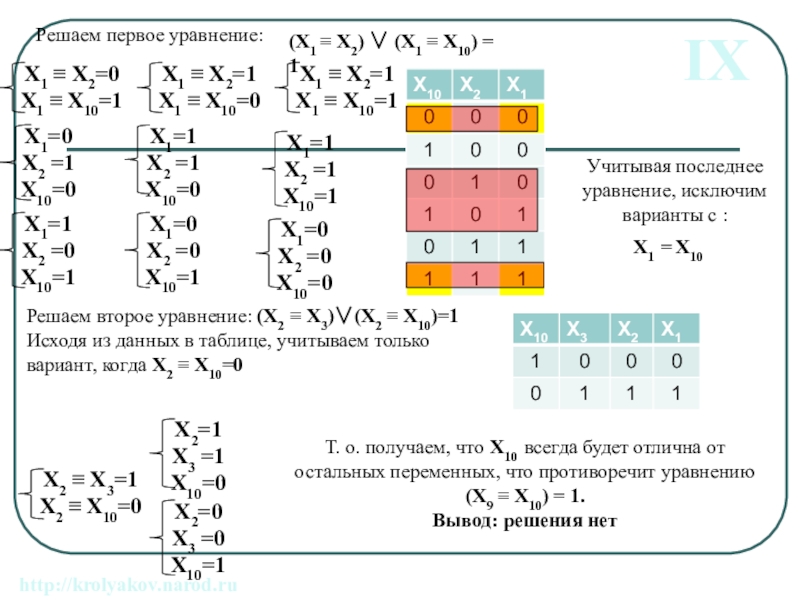
Слайд 28Решаем первое уравнение:
(X1 X2) (X1 X10) = 1
Решаем
Исходя из данных в таблице, учитываем только вариант, когда X2 X10=0
IX
http://krolyakov.narod.ru
Т. о. получаем, что X10 всегда будет отлична от остальных переменных, что противоречит уравнению (X9 X10) = 1.
Вывод: решения нет
Слайд 29Сколько различных решений имеет система уравнений
((X1 X2) (X3
((X3 X4) (X5 X6)) (¬(X3 X4) ¬(X5 X6)) = 1
((X5 X6) (X7 X8)) (¬(X5 X6) ¬(X7 X8)) = 1
((X7 X8) (X9 X10)) (¬(X7 X8) ¬(X9 X10)) = 1
где x1, x2, …, x10 – логические переменные?
В15
2012 г
Решаем самостоятельно
http://krolyakov.narod.ru
Введем обозначение
сложных переменных:
Y1 = (X1 X2)
Y2= (X3 X4)
Y3 = (X5 X6)
Y4 = (X7 X8)
Y5 = (X9 X10)
Запишем систему уравнений:
(Y1 Y2) (¬ Y1 ¬ Y2) = 1
(Y2 Y3) (¬ Y2 ¬ Y3) = 1
(Y3 Y4) (¬ Y3 ¬ Y4) = 1
(Y4 Y5) (¬ Y4 ¬ Y5) = 1
Слайд 30Cистема имеет 2 варианта решения.
В15
2012 г
Упростим уравнения:
¬(Y1 Y2 ) =
¬(Y2 Y3 ) = 1
¬(Y3 Y4 ) = 1
¬(Y4 Y5 ) = 1
Кол-во комбинаций для одного варианта решений: N=25=32
Всего решений: 32*2=64
http://kpolyakov.narod.ru
(Y1 ¬ Y1) (Y1 ¬Y2) (Y2 ¬Y1) (Y2 ¬ Y2) = 1
(Y1 ¬Y2) (Y2 ¬Y1) = 1
¬ (A B) = (¬ A B) (A ¬ B )
Решение