- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Рекурсия
Содержание
- 1. Рекурсия
- 2. РЕКУРСИЯСпособ обращения процедуры или функции к самой себе называется рекурсией.Вычисление факториала числа Числа ФибоначчиЗолотое сечение
- 3. Вычисление факториала числа Nn!=1*2*3*4*5…*n
- 4. function factorial(n: byte): longint;begin if n
- 5. Слайд 5
- 6. PROGRAM FACTORIAL_2; {Вычисление с помощью процедуры} USES
- 7. Слайд 7
- 8. Числа ФибоначчиВ 1202 году итальянский математик Фибоначчи
- 9. Чи́сла Фибона́ччи — элементы числовой последовательности1, 1, 2,
- 10. 1, 1, 2, 3, 5, 8, 13,
- 11. Эта последовательность была исследована Леонардо Пизанским, известным
- 12. Function FIB ( n : integer )
- 13. program fibonachchi;var i:integer; function fib(n:integer): longint;begin if n
- 14. PROGRAM KROLIKI; USES CRT; VAR
- 15. Слайд 15
- 16. Золотое сечение - это такое пропорциональное деление
- 17. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью
- 18. {Значение золотого сечения по заданному n} function
- 19. A:= A - BначалонетA Bконецввод A,Bвывод
- 20. ЗадачаДаны три натуральных числа. Найти НОД наибольшего
- 21. FUNCTION HOD(A,B:INTEGER):INTEGER; begin IF A=B THEN HOD:=A
- 22. Слайд 22
- 23. PROGRAM K8_V9_1;{Найти НОД наибольшего и наименьшего
- 24. Слайд 24
Слайд 2РЕКУРСИЯ
Способ обращения процедуры или функции к самой себе называется рекурсией.
Вычисление факториала
Числа Фибоначчи
Золотое сечение
Слайд 3Вычисление факториала числа N
n!=1*2*3*4*5…*n
(n-1)! n, если n>1
n! =
5!= 1*2*3*4*5 =(1*2*3*4)*5 = 4! *5
15!= 1*2*3*…*15 =(1*2*..*14)*15 = = 14! * 15
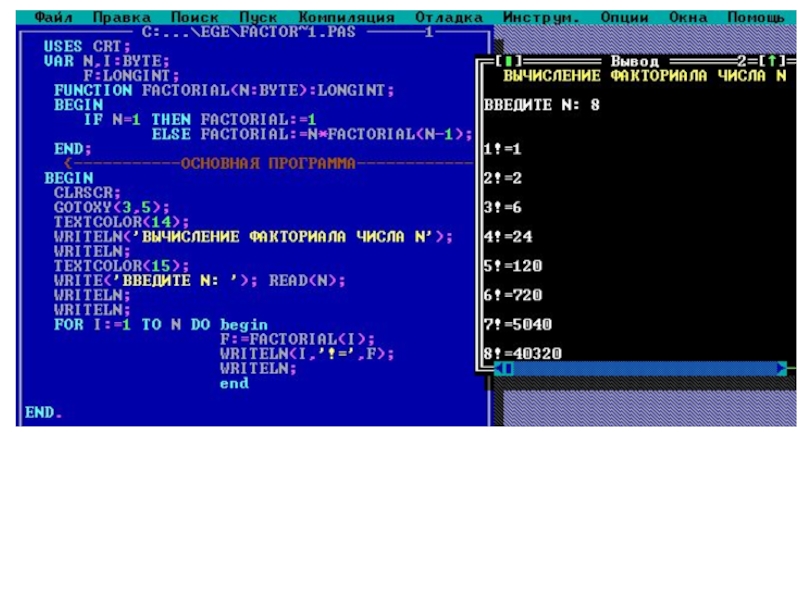
Слайд 4function factorial(n: byte): longint;
begin
if n = 1 then
else factorial := n * factorial (n - 1);
end;
Вызов в программе:
X:=factorial(5); write(X);
120
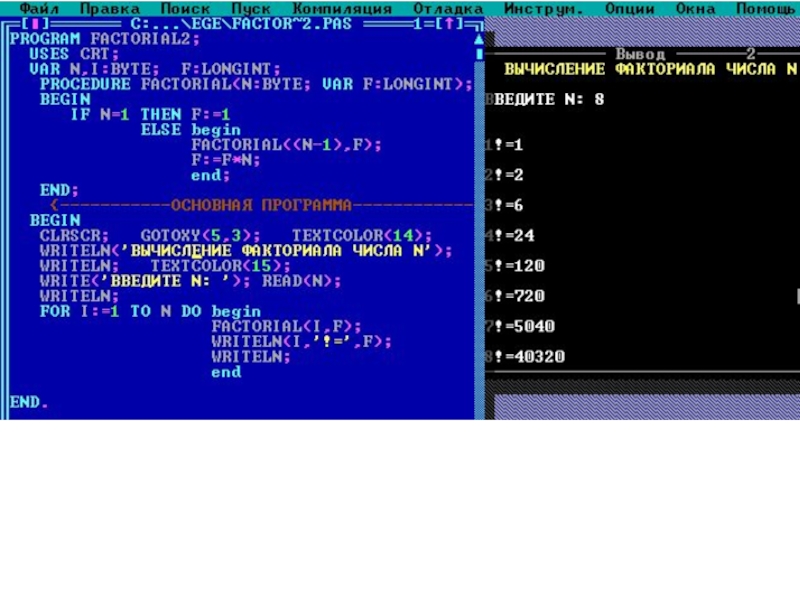
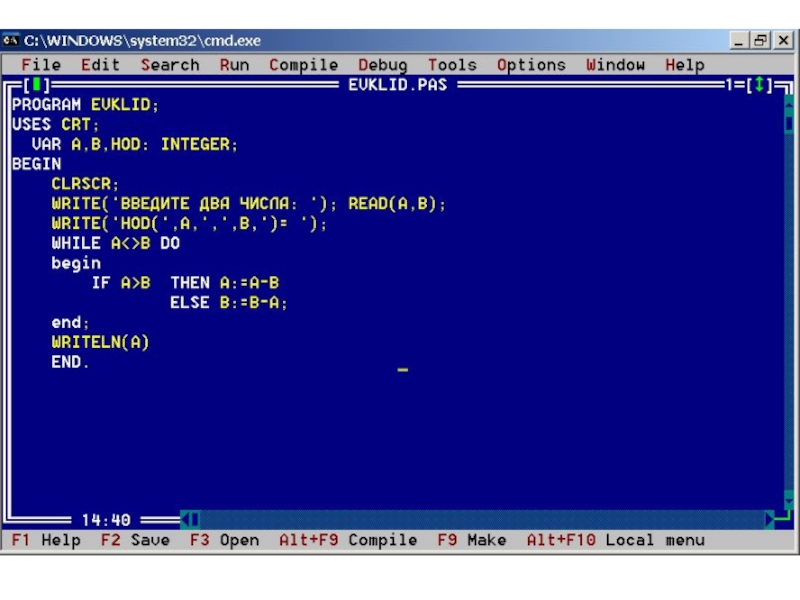
Слайд 6PROGRAM FACTORIAL_2;
{Вычисление с помощью процедуры}
USES CRT;
VAR N,I:BYTE; F:LONGINT;
begin
IF N=1 THEN FACTORIAL:=1
ELSE begin
FACTORIAL(N-1;F);
F:=F*N;
end;
end;
{-----------ОСНОВНАЯ ПРОГРАММА------------}
BEGIN
CLRSCR;
WRITELN('ВЫЧИСЛЕНИЕ ФАКТОРИАЛА ЧИСЛА N');
WRITE('ВВЕДИТЕ N: '); READ(N);
FOR I:=1 TO N DO begin
FACTORIAL(I,F);
WRITELN( I, '!=', F);
end
END.
Слайд 8Числа Фибоначчи
В 1202 году итальянский математик Фибоначчи решил такую задачу:
Пара кроликов
Сколько кроликов будет через год, если в начале года имелась пара кроликов?
Слайд 9Чи́сла Фибона́ччи — элементы числовой последовательности
1, 1, 2, 3, 5, 8, 13,
в которой каждое последующее число равно сумме двух предыдущих чисел.
Название по имени
средневекового математика
Леонардо Пизанского
(или Фибоначчи) .
Слайд 101, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,
каждое последующее число равно сумме двух предыдущих чисел.
Последовательность чисел Фибоначчи задается рекуррентным соотношением:
F1 =1 F2 =1 Fn = Fn -1 + Fn - 2
Слайд 11Эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его
Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
В «нулевом» месяце имеется пара кроликов (0 новых пар).
В первом месяце первая пара производит на свет другую пару (1 новая пара).
Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).
1,1,2,3,5,8…
F(n) = F(n — 1) + F(n — 2).
Слайд 12Function FIB ( n : integer ) :integer;
begin
if (n=1) or
else FIB:=FIB(n-2)+FIB(n-1)
end;
Слайд 13program fibonachchi;
var i:integer;
function fib(n:integer): longint;
begin
if n
else fib:=fib(n-1)+fib(n-2);
end;
begin
for i:=1 to 12 do writeln('fib(', i, ') = ', fib(i) );
end.
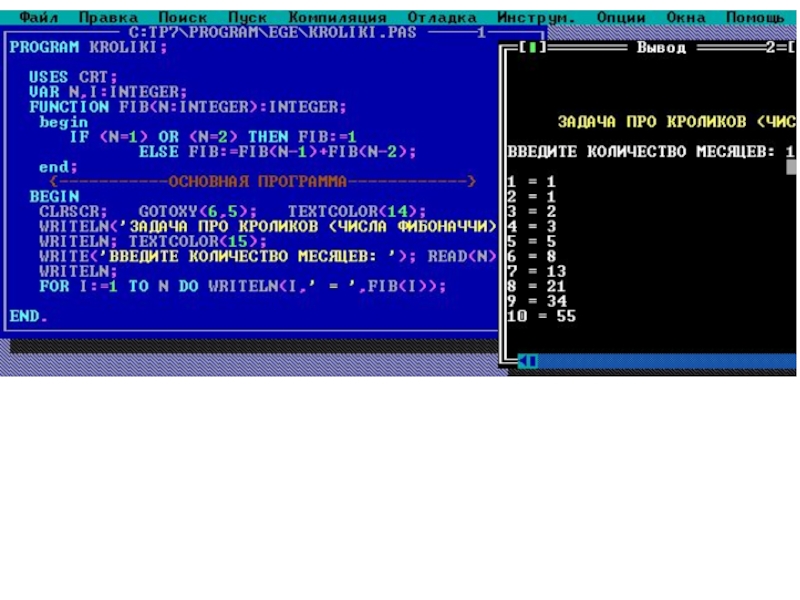
Слайд 14PROGRAM KROLIKI;
USES CRT;
VAR N,I:INTEGER;
FUNCTION FIB(N:INTEGER):INTEGER;
begin
IF (N=1) OR (N=2) THEN FIB:=1
ELSE FIB:=FIB(N-1)+FIB(N-2);
end;
{-----------ОСНОВНАЯ ПРОГРАММА------------}
BEGIN
CLRSCR;
WRITELN('ЗАДАЧА ПРО КРОЛИКОВ (ЧИСЛА ФИБОНАЧЧИ)');
WRITE('ВВЕДИТЕ КОЛИЧЕСТВО МЕСЯЦЕВ: '); READ(N);
FOR I:=1 TO N DO WRITELN(I,' = ',FIB(I));
END.
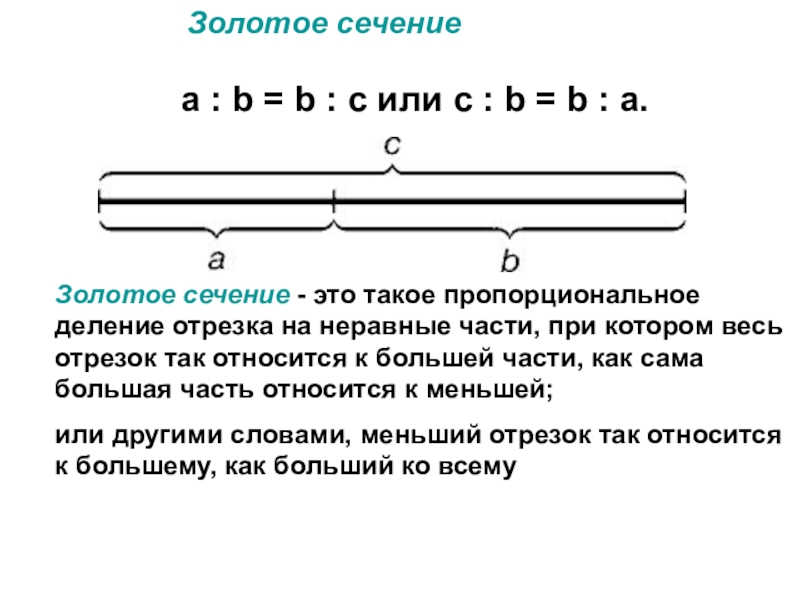
Слайд 16Золотое сечение - это такое пропорциональное деление отрезка на неравные части,
или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.
Золотое сечение
Слайд 17Отрезки золотой пропорции выражаются бесконечной иррациональной дробью 0,618..., если c принять
Числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи.
На этой пропорции базируются основные геометрические фигуры.
Любой отрезок может быть разделен таким образом,
что соотношение между его меньшей и большей частями будет равно отношению между большей частью и всем отрезком .
Это отношение всегда равно 0.618.
Слайд 18{Значение золотого сечения по заданному n}
function sech(n:integer):real;
begin
end;
var i : integer;
begin
writeln('u(1) = ',fib(1));
for i:=2 to nmax do
writeln('u(',i,') = ',fib(i),' v(',i,') = ',sech(i));
end.
значение золотого сечения V(n) = u(n) / u(n-1)
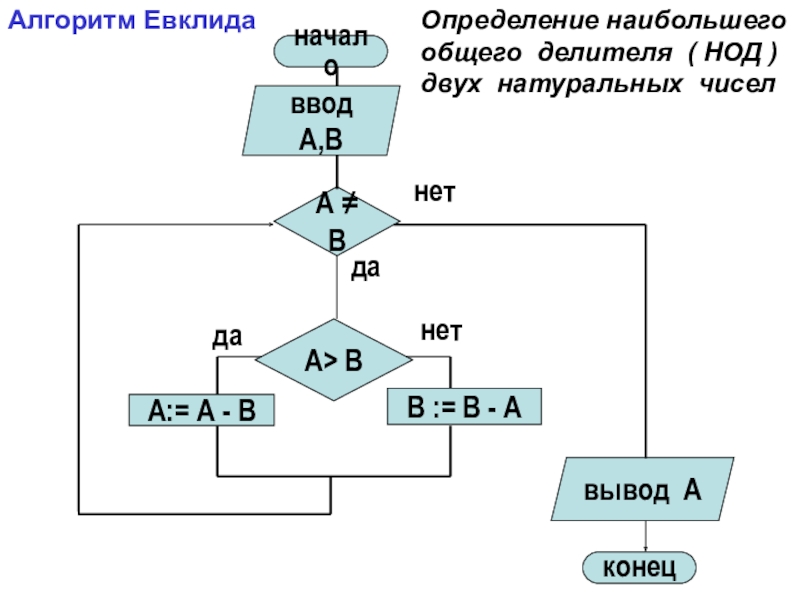
Слайд 19A:= A - B
начало
нет
A B
конец
ввод A,B
вывод A
A> B
B := B
да
да
нет
Алгоритм Евклида
Определение наибольшего общего делителя ( НОД )
двух натуральных чисел
Слайд 20Задача
Даны три натуральных числа. Найти НОД наибольшего и наименьшего из этих
ВВЕДИТЕ ТРИ ЧИСЛА: 18 24 36
Наименьшее число: 18
Наибольшее число: 36
НОД(18,36)=9
ВВЕДИТЕ ТРИ ЧИСЛА: 48 24 36
Наименьшее число: 24
Наибольшее число: 48
НОД(24,48)=24
Слайд 21FUNCTION HOD(A,B:INTEGER):INTEGER;
begin
IF A=B THEN HOD:=A
else HOD:=HOD(A,B-A);
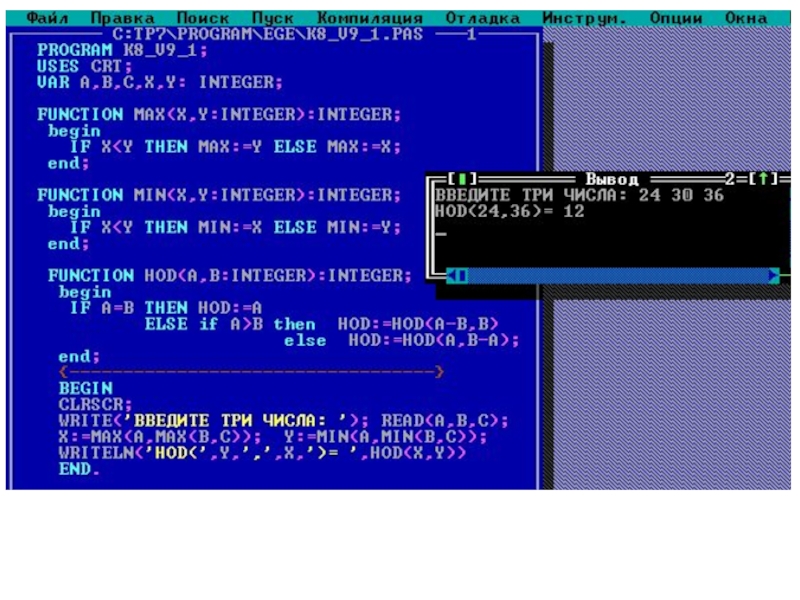
Слайд 23 PROGRAM K8_V9_1;
{Найти НОД наибольшего и наименьшего из трех чисел}
USES
VAR A, B, C, X, Y: INTEGER;
FUNCTION MAX(X,Y:INTEGER):INTEGER;
begin
IF X
FUNCTION MIN(X,Y:INTEGER):INTEGER;
begin
IF X
FUNCTION HOD(A,B:INTEGER):INTEGER;
begin
IF A=B THEN HOD:=A
ELSE if A>B then HOD:=HOD(A-B,B) else HOD:=HOD(A,B-A);
end;
BEGIN
CLRSCR;
WRITE('ВВЕДИТЕ ТРИ ЧИСЛА: '); READ(A,B,C);
X:=MAX(A,MAX(B,C)); Y:=MIN(A,MIN(B,C));
WRITELN('HOD(',Y,',',X,')= ',HOD(X,Y))
END.