ВО «ВТППП», группа ПК15-05, 2 курс
Руководитель: Шишлова Е. Н., преподаватель информатики и
математики, высшая категория.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проектная работа по информатикеЗагадочный биспорядок:история и применение фракталов
Содержание
- 1. Проектная работа по информатикеЗагадочный биспорядок:история и применение фракталов
- 2. Гипотеза: если изучить закономерность построения фрактала, то
- 3. Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия (объект,
- 4. Первые примеры самоподобных множеств с необычными свойствами
- 5. Термин «фрактал» введён Бенуа Мандельбротом в 1995 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы».
- 6. В 1975 году Мандельброт опубликовал свою работу Какова
- 7. Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.
- 8. КЛАССИФИКАЦИЯ ФРАКТАЛОВ Геометрические фракталыСтохастические фракталыАлгебраические фракталы
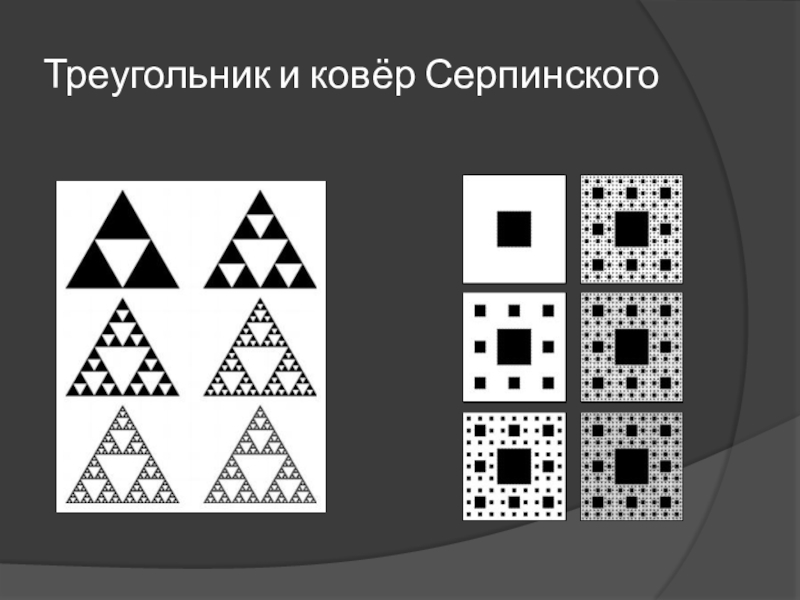
- 9. Треугольник и ковёр Серпинского
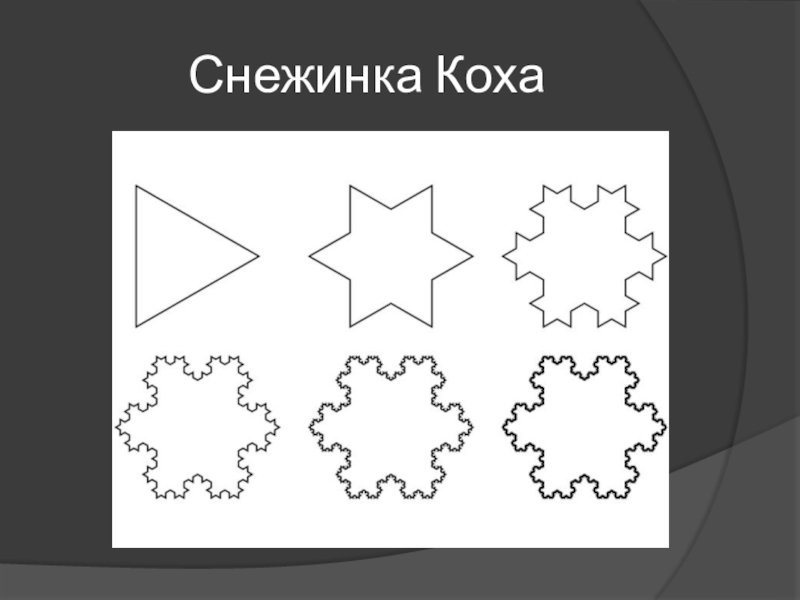
- 10. Снежинка Коха
- 11. Кривая дракона
- 12. Алгебраические фракталыМножество Жюлиамножество Мандельброта
- 13. Стохастические фракталы форма горыформа облака
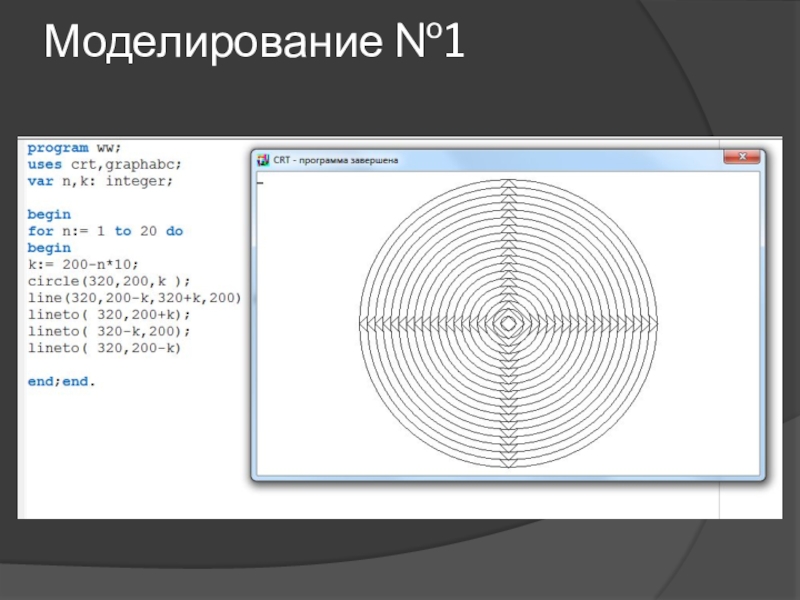
- 14. Моделирование №1
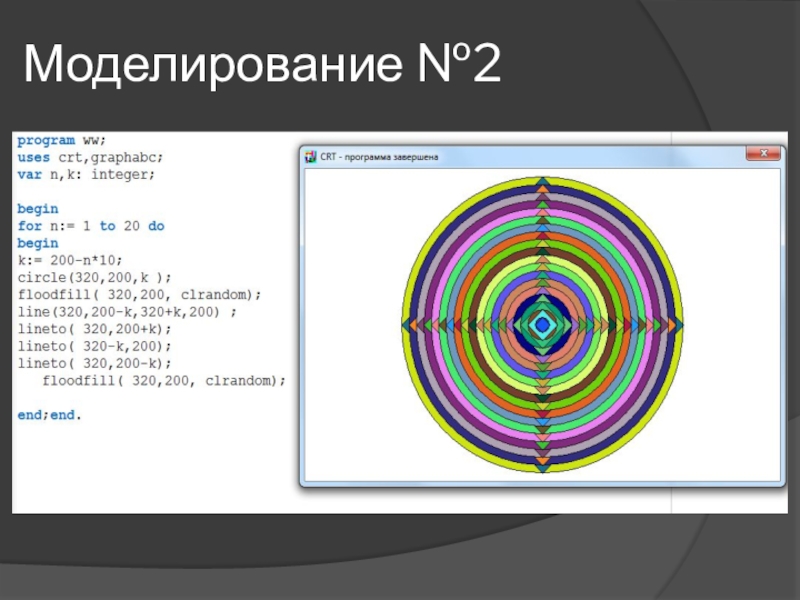
- 15. Моделирование №2
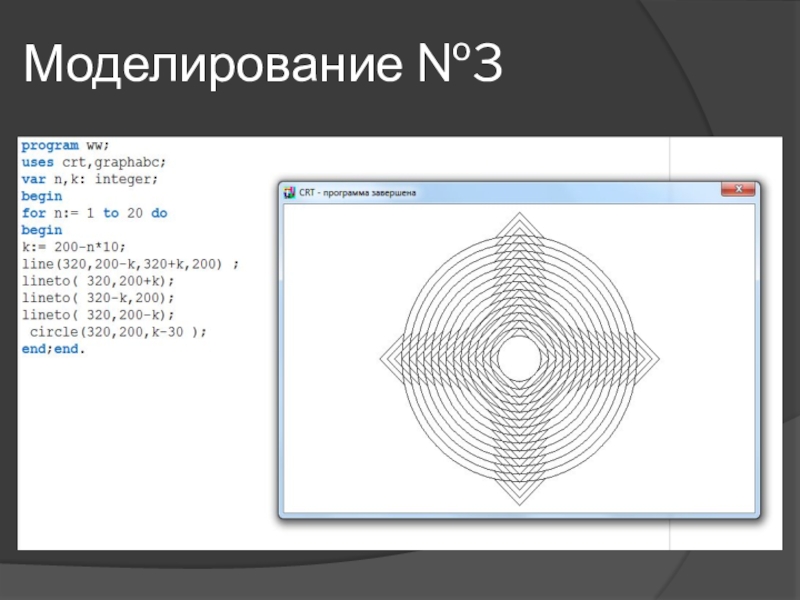
- 16. Моделирование №3
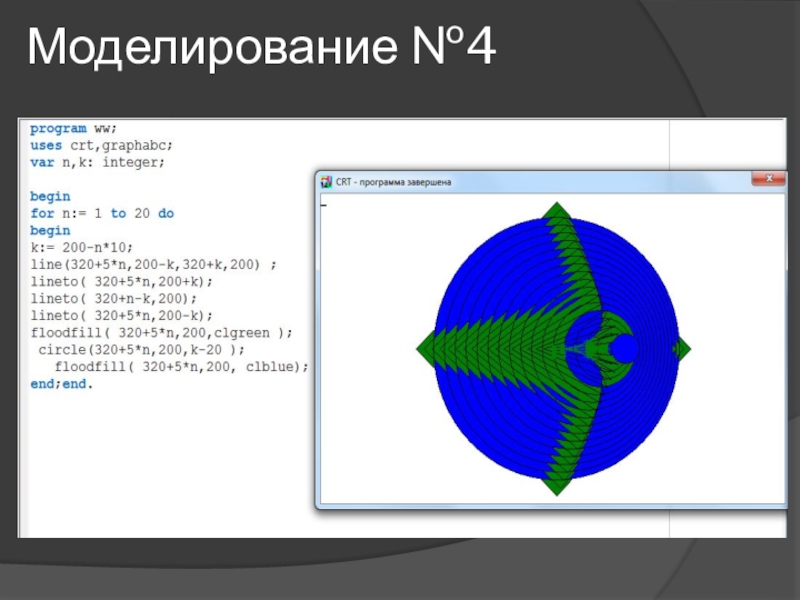
- 17. Моделирование №4
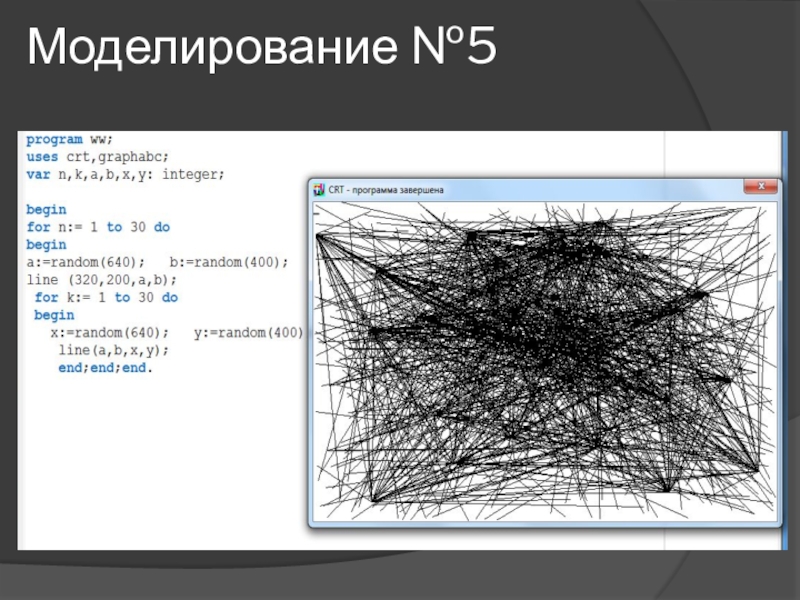
- 18. Моделирование №5
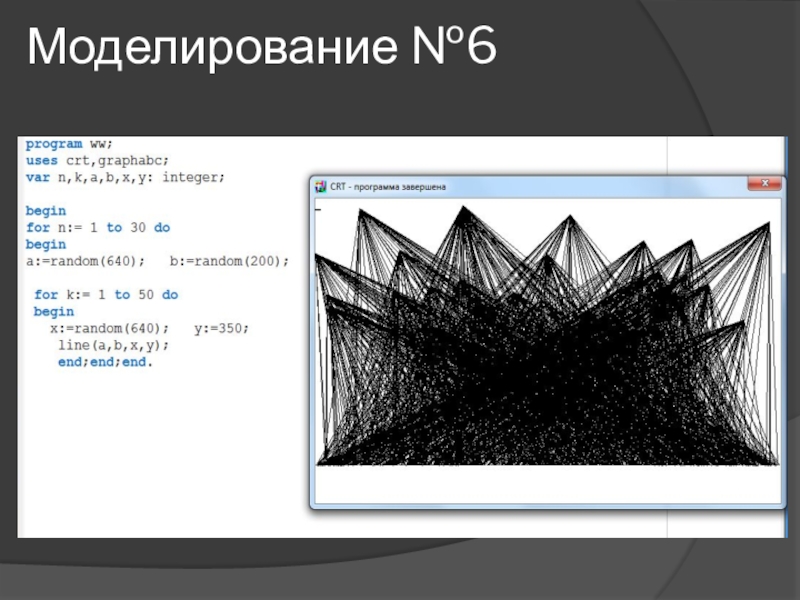
- 19. Моделирование №6
- 20. Природные объекты, обладающие фрактальными свойствамиВ живой природе:В
- 21. Где применяется фрактальная графика?
- 22. Кондитерские изделия, десерты
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Ковры
- 27. Слайд 27
- 28. Слайд 28
- 29. Одежда, обувь
- 30. Слайд 30
- 31. Слайд 31
- 32. Обои
- 33. Слайд 33
- 34. Постельные комплекты, ткани
- 35. Слайд 35
- 36. Слайд 36
- 37. Посуда
- 38. Слайд 38
- 39. Слайд 39
- 40. Фрактальная графика - это не просто множество
- 41. Спасибо за внимание!
Гипотеза: если изучить закономерность построения фрактала, то можно смоделировать фракталы в прикладных программах, можно использовать их в профессиональной деятельности.Цель: исследовать фракталы и составить программы моделирования фракталов.Задачи: узнать, что такое фракталы;изучить историю возникновения и развития фрактальной геометрии
Слайд 2Гипотеза:
если изучить закономерность построения фрактала, то можно смоделировать фракталы в
прикладных программах, можно использовать их в профессиональной деятельности.
Цель:
исследовать фракталы и составить программы моделирования фракталов.
Задачи:
узнать, что такое фракталы;
изучить историю возникновения и развития фрактальной геометрии и графики;
изучить классификацию фракталов;
найти информацию о фракталах в явлениях природы и их применении в жизни;
смоделировать фракталы на языке программирования Pascal АВС.
Актуальность:
Интерес к проблеме обусловлен интересом к компьютерной графики
Результат исследования:
Разработка программ построения фракталов на языке программирования Pascal АВС и применение их в профессиональной деятельности.
Цель:
исследовать фракталы и составить программы моделирования фракталов.
Задачи:
узнать, что такое фракталы;
изучить историю возникновения и развития фрактальной геометрии и графики;
изучить классификацию фракталов;
найти информацию о фракталах в явлениях природы и их применении в жизни;
смоделировать фракталы на языке программирования Pascal АВС.
Актуальность:
Интерес к проблеме обусловлен интересом к компьютерной графики
Результат исследования:
Разработка программ построения фракталов на языке программирования Pascal АВС и применение их в профессиональной деятельности.
Слайд 3Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия (объект, в точности или приближённо
совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей).
Слайд 4Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке
в результате изучения непрерывных недифференцируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора).
Слайд 5Термин «фрактал» введён Бенуа Мандельбротом в 1995 году и получил широкую известность с выходом в 1977
году его книги «Фрактальная геометрия природы».
Слайд 6В 1975 году Мандельброт опубликовал свою работу Какова длина побережья Великобритании? — первое
исследование фракталов. Понятие «фрактал» придумал сам Бенуа Мандельброт (от лат. fractus, означающего «сломанный, разбитый»). Используя находящиеся в его распоряжении компьютеры IBM, Мандельброт создал графические изображения, сформированные на основе множества Мандельброта. По словам математика, он не чувствовал себя изобретателем, несмотря на то, что никто до него не создавал ничего подобного.
Слайд 7
Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.
Слайд 8КЛАССИФИКАЦИЯ ФРАКТАЛОВ
Геометрические фракталы
Стохастические фракталы
Алгебраические фракталы
Слайд 20Природные объекты, обладающие фрактальными свойствами
В живой природе:
В неживой природе:
Кораллы
Морские звезды и ежи
Морские раковины
Цветы
и растения (брокколи, капуста)
Кроны деревьев и листья растений
Плоды (ананас)
Кроны деревьев и листья растений
Плоды (ананас)
Границы географических объектов (стран, областей, городов)
Береговые линии
Горные хребты
Снежинки
Облака
Молнии
Морозные узоры на оконных стёклах
Кристаллы
Сталактиты, сталагмиты, геликтиты.
Слайд 40Фрактальная графика - это не просто множество самоповторяющихся изображений, это модель
структуры и принципа любого сущего. Вся наша жизнь представлена фракталами. Не только визуальными, но ещё и структурными, отражающими нашу жизнь