- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад у практическому занятию по информатике Использование различных возможностей электронных таблиц: моделирование статистического прогнозирования
Содержание
- 1. Презентация у практическому занятию по информатике Использование различных возможностей электронных таблиц: моделирование статистического прогнозирования
- 2. Цели урока: Образовательные:формирование у обучающихся умений применять,
- 3. Результаты:Личностные:готовность и способность к самостоятельной и ответственной
- 4. Моделирование статистического прогнозированияСтатистика — наука о сборе,
- 5. Моделирование статистического прогнозированияСамым простым для моделирования является
- 6. Моделирование статистического прогнозированияДанные о загрязнённости воздуха угарным
- 7. Моделирование статистического прогнозированияГрафик искомой функции должен проходить
- 8. Моделирование статистического прогнозированияА как построить математическую модель
- 9. Моделирование статистического прогнозированияОсновные требования к искомой функции:-
- 10. Метод наименьших квадратовПолучение регрессионной модели происходит в
- 11. Метод наименьших квадратовЧаще всего выбор производится среди
- 12. Метод наименьших квадратовЕсли вы выбрали (сознательно или
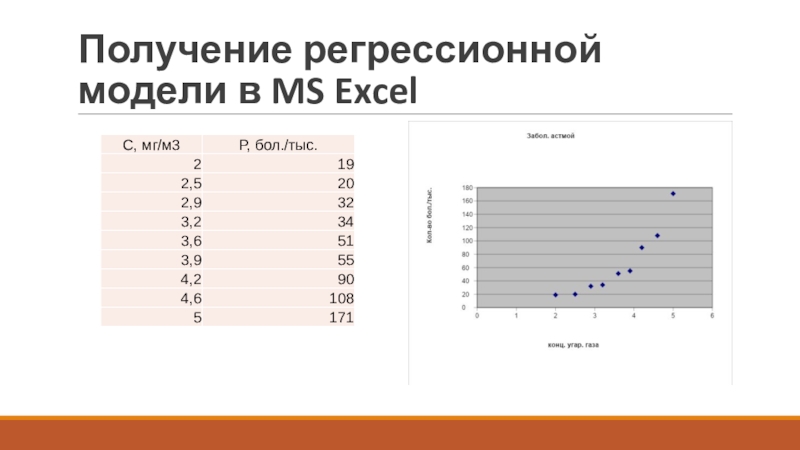
- 13. Получение регрессионной модели в MS Excel
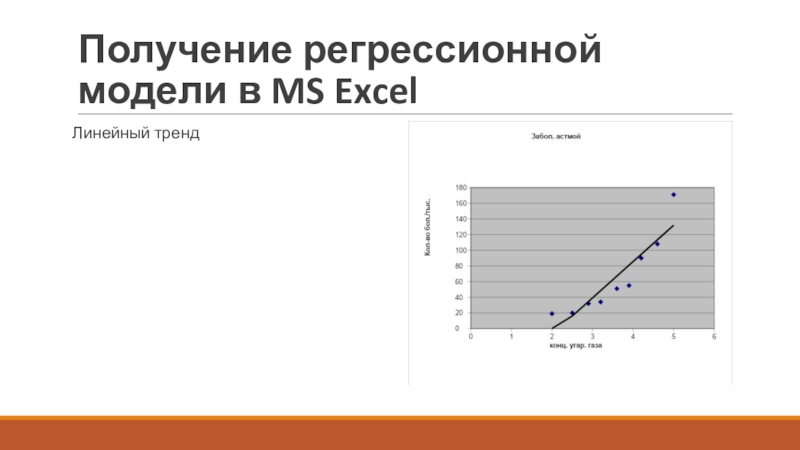
- 14. Получение регрессионной модели в MS ExcelЛинейный тренд
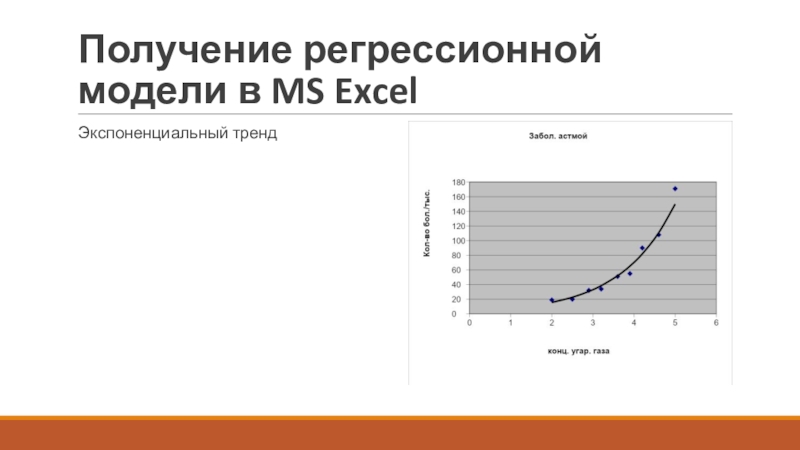
- 15. Получение регрессионной модели в MS ExcelЭкспоненциальный тренд
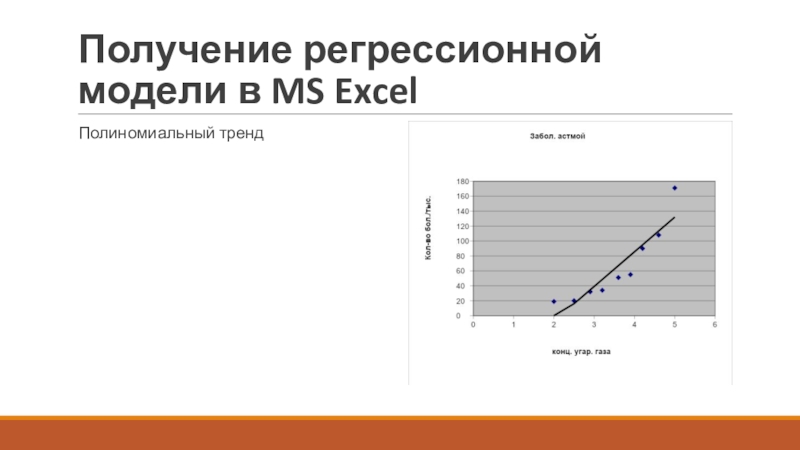
- 16. Получение регрессионной модели в MS ExcelПолиномиальный тренд
- 17. Прогнозирование по регрессионной моделиСуществует два способа прогнозов
- 18. Прогнозирование по регрессионной модели Прогнозирование способом восстановления значения
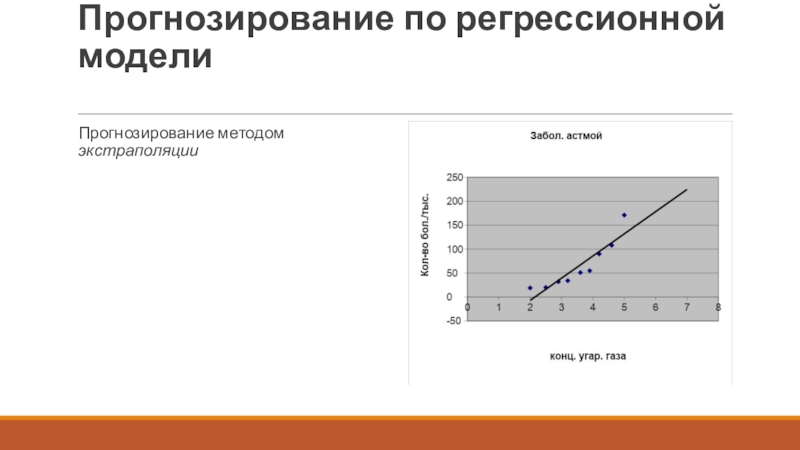
- 19. Прогнозирование по регрессионной модели Прогнозирование методом экстраполяции
Цели урока: Образовательные:формирование у обучающихся умений применять, анализировать, преобразовывать информационные модели реальных объектов и процессов, используя при этом ИКТ, в том числе при изучении других дисциплин;владение информационной культурой, способностью анализировать и оценивать информацию с использованием информационно-коммуникационных
Слайд 1Использование различных возможностей электронных таблиц: моделирование статистического прогнозирования
Практическое занятие
Слайд 2Цели урока:
Образовательные:
формирование у обучающихся умений применять, анализировать, преобразовывать информационные модели
реальных объектов и процессов, используя при этом ИКТ, в том числе при изучении других дисциплин;
владение информационной культурой, способностью анализировать и оценивать информацию с использованием информационно-коммуникационных технологий, средств образовательных и социальных коммуникаций.
Воспитательные:
вовлечь в активную практическую деятельность
Развивающие:
активизировать познавательную активность при создании регрессивных моделей;
владение информационной культурой, способностью анализировать и оценивать информацию с использованием информационно-коммуникационных технологий, средств образовательных и социальных коммуникаций.
Воспитательные:
вовлечь в активную практическую деятельность
Развивающие:
активизировать познавательную активность при создании регрессивных моделей;
Слайд 3Результаты:
Личностные:
готовность и способность к самостоятельной и ответственной творческой деятельности с использованием
информационно-коммуникационных технологий;
Метапредметные:
умение анализировать и представлять информацию, данную в электронных форматах на компьютере в различных видах;
умение публично представлять результаты собственного исследования, вести дискуссии, доступно и гармонично сочетая содержание и формы представляемой информации средствами информационных и коммуникационных технологий;
Предметные:
владение способами представления, хранения и обработки данных на компьютере;
владение компьютерными средствами представления и анализа данных в электронных таблицах;
сформированность базовых навыков и умений по соблюдению требований техники безопасности, гигиены и ресурсосбережения при работе со средствами информатизации;
Метапредметные:
умение анализировать и представлять информацию, данную в электронных форматах на компьютере в различных видах;
умение публично представлять результаты собственного исследования, вести дискуссии, доступно и гармонично сочетая содержание и формы представляемой информации средствами информационных и коммуникационных технологий;
Предметные:
владение способами представления, хранения и обработки данных на компьютере;
владение компьютерными средствами представления и анализа данных в электронных таблицах;
сформированность базовых навыков и умений по соблюдению требований техники безопасности, гигиены и ресурсосбережения при работе со средствами информатизации;
Слайд 4Моделирование статистического прогнозирования
Статистика — наука о сборе, измерении и анализе массовых
количественных данных.
Статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер, но верно отражают характер зависимости величин.
И еще одно важное замечание: для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.
Статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер, но верно отражают характер зависимости величин.
И еще одно важное замечание: для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.
Слайд 5Моделирование статистического прогнозирования
Самым простым для моделирования является объект, у которого один
входной и один выходной фактор.
Входной фактор характеризует воздействие на исследуемый объект. В технологических процессах машиностроения это могут быть температура, сила, время, геометрические параметры инструмента, характеристики обрабатываемого и инструментального материалов и т. д.
Выходной фактор характеризует реакцию объекта на воздействие входного фактора. Выходные факторы в технологических процессах машиностроения – длина пройденного инструментом пути, величина износа, напряжения, качество обработанной поверхности и т. д.
Входной фактор характеризует воздействие на исследуемый объект. В технологических процессах машиностроения это могут быть температура, сила, время, геометрические параметры инструмента, характеристики обрабатываемого и инструментального материалов и т. д.
Выходной фактор характеризует реакцию объекта на воздействие входного фактора. Выходные факторы в технологических процессах машиностроения – длина пройденного инструментом пути, величина износа, напряжения, качество обработанной поверхности и т. д.
Слайд 6Моделирование статистического прогнозирования
Данные о загрязнённости воздуха угарным газом полученные экспериментальным путем
в различных населенных пунктах какого то региона
Слайд 7Моделирование статистического прогнозирования
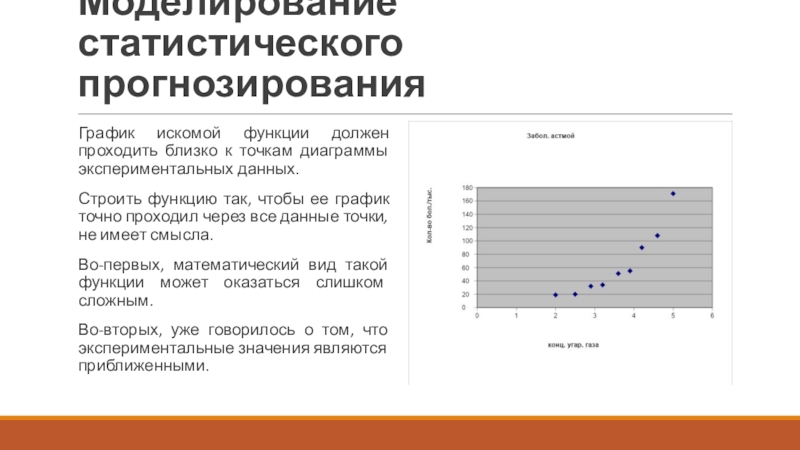
График искомой функции должен проходить близко к точкам диаграммы
экспериментальных данных.
Строить функцию так, чтобы ее график точно проходил через все данные точки, не имеет смысла.
Во-первых, математический вид такой функции может оказаться слишком сложным.
Во-вторых, уже говорилось о том, что экспериментальные значения являются приближенными.
Строить функцию так, чтобы ее график точно проходил через все данные точки, не имеет смысла.
Во-первых, математический вид такой функции может оказаться слишком сложным.
Во-вторых, уже говорилось о том, что экспериментальные значения являются приближенными.
Слайд 8Моделирование статистического прогнозирования
А как построить математическую модель данного явления?
Нужно получить формулу,
отражающую зависимость количества хронических больных Р от концентрации угарного газа С.
На языке математики это называется функцией зависимости Р от С: Р(С).
Вид такой функции неизвестен, ее следует искать методом подбора по экспериментальным данным.
На языке математики это называется функцией зависимости Р от С: Р(С).
Вид такой функции неизвестен, ее следует искать методом подбора по экспериментальным данным.
Слайд 9Моделирование статистического прогнозирования
Основные требования к искомой функции:
- она должна быть достаточно
простой для использования ее в дальнейших вычислениях;
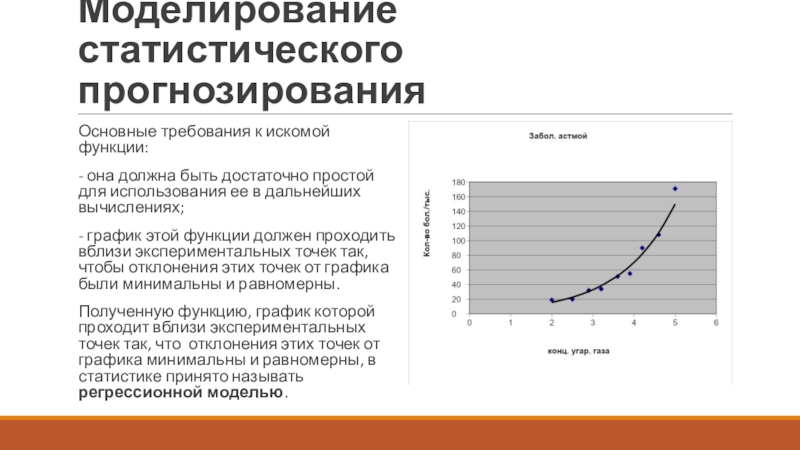
- график этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны.
Полученную функцию, график которой проходит вблизи экспериментальных точек так, что отклонения этих точек от графика минимальны и равномерны, в статистике принято называть регрессионной моделью.
- график этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны.
Полученную функцию, график которой проходит вблизи экспериментальных точек так, что отклонения этих точек от графика минимальны и равномерны, в статистике принято называть регрессионной моделью.
Слайд 10Метод наименьших квадратов
Получение регрессионной модели происходит в два этапа:
1 подбор вида
функции;
2 вычисление параметров функции.
Первая задача не имеет строгого решения. Здесь может помочь опыт и интуиция исследователя, а возможен и «слепой» перебор из конечного числа функций и выбор лучшей из них.
2 вычисление параметров функции.
Первая задача не имеет строгого решения. Здесь может помочь опыт и интуиция исследователя, а возможен и «слепой» перебор из конечного числа функций и выбор лучшей из них.
Слайд 11Метод наименьших квадратов
Чаще всего выбор производится среди следующих функций:
Квадратичная функция называется
в математике полиномом второй степени.
Во всех этих формулах х — аргумент, у — значение функции, а, b, с, d — параметры функции, ln(x) — натуральный логарифм, е — константа, основание натурального логарифма.
Во всех этих формулах х — аргумент, у — значение функции, а, b, с, d — параметры функции, ln(x) — натуральный логарифм, е — константа, основание натурального логарифма.
Слайд 12Метод наименьших квадратов
Если вы выбрали (сознательно или наугад) одну из предлагаемых
функций, то следующим шагом нужно подобрать параметры (а, Ь, с и пр.) так, чтобы функция располагалась как можно ближе к экспериментальным точкам.
Что значит «располагалась как можно ближе»?
Ответить на этот вопрос значит предложить метод вычисления параметров.
Такой метод был предложен в XVIII веке немецким математиком К. Гауссом.
Он называется методом наименьших квадратов (МНК). Суть его заключается в следующем: искомая функция должна быть построена так, чтобы сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции была минимальной.
Что значит «располагалась как можно ближе»?
Ответить на этот вопрос значит предложить метод вычисления параметров.
Такой метод был предложен в XVIII веке немецким математиком К. Гауссом.
Он называется методом наименьших квадратов (МНК). Суть его заключается в следующем: искомая функция должна быть построена так, чтобы сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции была минимальной.
Слайд 17Прогнозирование по регрессионной модели
Существует два способа прогнозов по регрессионной модели:
1 Если
прогноз производится в пределах экспериментальных значений независимой переменной (в нашем случае это концентрация угарного газа С), то это называется восстановлением значения.
2 Прогнозирование за пределами экспериментальных данных называется экстраполяцией.
2 Прогнозирование за пределами экспериментальных данных называется экстраполяцией.