По материалам сайта http://kpolyakov.spb.ru
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Разбор задания 16 ЕГЭ по информатике
Содержание
- 1. Презентация Разбор задания 16 ЕГЭ по информатике
- 2. Демо версии 2014, 2015, 2016
- 3. Что нужно знать:• принципы кодирования чисел в позиционных
- 4. Что нужно знать:• число 2N в двоичной системе
- 5. Легче объяснить:• число 10N в десятичной (более привычной!)
- 6. переход к другим с.с.:• число 3N в троичной
- 7. Общая схема:• число aN в с.с. c основанием
- 8. Пример с решением:Сколько значащих нулей содержится в
- 9. Примеры для самостоятельного решенияСколько единиц в двоичной
- 10. Сколько единиц в двоичной записи числа 42015
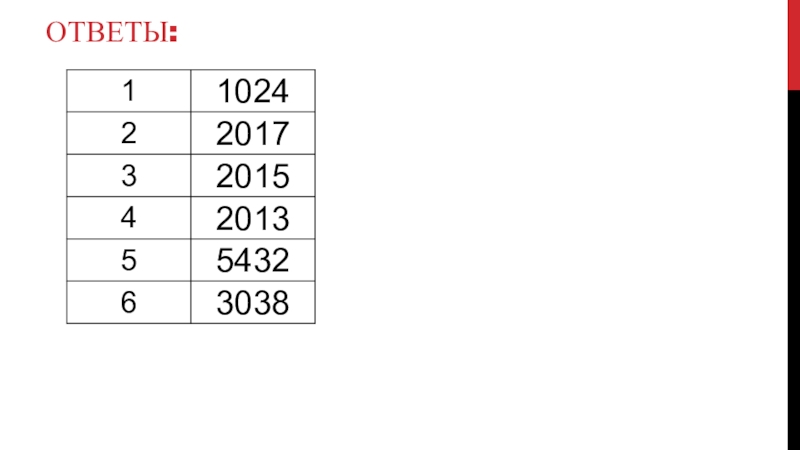
- 11. Ответы:
- 12. Пример с решением:713 единиц,1301 нуль1294 единиц, 6
- 13. Пример с решением:2 = 3 - 1Итого:
- 14. Пример с решением:1 пятерка,14 нулей8 пятерок, 2
- 15. Пример с решением:1 единица,379 нулей1 единица, 378
- 16. Пример с решением:1 единица,8800 нулей1 единица, 4400
- 17. Пример с решением:4400 единицИтого: 4400Сколько единиц в
- 18. Пример с решением:Итого: 1011101102 = 374Некоторое число
- 19. Пример с решением:Итого: 3Некоторое число X из
Слайд 1ЕГЭ
Задание 16
(повышенный уровень, время – 2 мин)
Тема: Кодирование чисел. Системы
Слайд 3Что нужно знать:
• принципы кодирования чисел в позиционных системах счисления;
• правила
• чтобы перевести число 12345N, из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на в степени, равной ее разряду:
4 3 2 1 0 ← разряды
1 2 3 4 5N = 1•N4 + 2•N3 + 3•N2 + 4•N1 + 5•N0
• последняя цифра записи числа в системе счисления с основанием N – это остаток от деления этого числа на N
• две последние цифры – это остаток от деления на N2, и т.д.
• двоичная арифметика (сложение, вычитание, умножение)
Слайд 4Что нужно знать:
• число 2N в двоичной системе записывается как единица и
2N = 10000….02
N
• число 2N-1 в двоичной системе записывается как N единиц:
2N - 1 = 11….12
N
• число 2N–2K при K < N в двоичной системе записывается как N–K единиц и K нулей:
2N - 2K = 11….100…002
N-K K
• 2N + 2N = 2*2N = 2N+1
2N = 2N+1 - 2N
- 2N = - 2N+1 + 2N
Слайд 5Легче объяснить:
• число 10N в десятичной (более привычной!) системе записывается как единица
10N=10000….010 Пример: 104=10000
N
• число 10N-1 в десятичной системе записывается как N девяток (!):
10N-1=99….910 Пример: 104-1= 9999
N
• число 10N–10K при K < N в десятичной системе записывается как N–K девяток и K нулей:
10N-10K=99….900…0010 Пример: 105-102= 100000
N-K K 100
99900
5-2=3
2
Слайд 6переход к другим с.с.:
• число 3N в троичной системе записывается как единица
3N = 10000….03
N
• число 3N-1 в троичной системе записывается как N двоек:
3N – 1 = 222...23
N
• число 3N–3K при K < N в троичной системе записывается как N–K двоек и K нулей:
3N - 3K = 222…200…003
N-K K
Слайд 7Общая схема:
• число aN в с.с. c основанием a записывается как единица
aN = 10000….0a
N
• число aN-1 в с.с. c основанием a записывается как N раз (a-1):
aN - 1 = (a-1)(a-1)…(a-1)a
N
• число aN–aK при K < N в с.с. основанием a записывается как N–K (a-1) и K нулей:
aN – aK = (a-1)(a-1)…(a-1)00…00a
N-K K
Слайд 8Пример с решением:
Сколько значащих нулей содержится в двоичной записи числа, которое
8510 + 41500-16 ?
Алгоритм:
Все переводим в степени двойки;
NB! Как представить 16?
Выстраиваем всю запись по возрастанию степени (!!!);
23000 + 21530 – 24 =
2 3000 = 100000…000 (1 и 3000 нулей)
21534 - 24 = 11111…1111 0000 (1530 единиц и 4 нуля)
Получаем в результате сложения: 100000…00011111….11110000
Нулей: 3000 – 1530 + 4 = 1474
Слайд 9Примеры для самостоятельного решения
Сколько единиц в двоичной записи числа 81023 +
3 = 4-1, 23069 + 21024 – 22 +20 !!! Избегать большого количества «-»
Сколько единиц в двоичной записи числа 42016 + 22018 – 6?
6 = 8 – 2, 24032 + 22018 – 23 +21
Сколько единиц в двоичной записи числа 42014 + 22015 – 9?
24028 + 22015 – 10012
Слайд 10Сколько единиц в двоичной записи числа 42015 + 22015 – 15?
Сколько единиц в двоичной записи числа 82014 – 2614 + 45?
45 = 1011012 , 26042 – 2614 + 1011012
Сколько единиц в двоичной записи числа 81014 – 2530 – 12?
12 = 11002, 23042 – 2530 – 11002
Слайд 12Пример с решением:
713 единиц,
1301 нуль
1294 единиц,
6 нулей
Итого: 713 + 1294
2 единицы,
3 нуля
1 единица,
1 нуль
Использование - 2N = - 2N+1 + 2N
Сколько единиц в двоичной записи числа 22014 – 4650 – 38?
Слайд 13Пример с решением:
2 = 3 - 1
Итого: 4
4 двойки,
1 нуль
1
Значение арифметического выражения: 98 + 35 – 2 – записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
1 единица,
16 нулей
Слайд 14Пример с решением:
1 пятерка,
14 нулей
8 пятерок,
2 нуля
Итого: 8 + 1
Значение арифметического выражения: 5∙367 + 610 – 36 записали в системе счисления с основанием 6. Сколько цифр «5» содержится в этой записи?
Слайд 15Пример с решением:
1 единица,
379 нулей
1 единица,
378 нулей
Итого: 11102=E16
3 единицы,
377
Какая первая цифра в шестнадцатеричной записи числа 2379+2378+2377?
11100000……….00002 переводим в 16 с.с. с помощью тетрад: 377:4 = 94 и 1 «0» в остатке
1 единица,
377 нулей
Слайд 16Пример с решением:
1 единица,
8800 нулей
1 единица,
4400 нулей
Итого: 1 +4399 =
1 единица,
1 нуль
Сколько единиц в двоичной записи числа (24400 – 1)·(42200 + 2)?
24400 – 21 =1111111….11110
4399
Слайд 17Пример с решением:
4400 единиц
Итого: 4400
Сколько единиц в двоичной записи числа (24400
1111
1010
1111
1111
1001011
Количество единиц не меняется!
Слайд 18Пример с решением:
Итого: 1011101102 = 374
Некоторое число X из десятичной системы
X= *7*16 = 5*68 = ***1*4
Определите число X.
Представим все числа в 2 с.с.
*7*16 = * * * * 0111 * * * *2
5*68 = 101 * * * 1 1 02
***1*4= * * * * * * 0 1 * *2
1011101102
Слайд 19Пример с решением:
Итого: 3
Некоторое число X из десятичной системы счисления перевели
X = *516 = *0*8.
Сколько чисел соответствуют условию задачи?
Представим все числа в 2 с.с.
*516 = * * * *01 012
*0*8 = * * * 000 * * *2
* * 000101 2
00
01
10
11