- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Представление чисел в компьютере
Содержание
- 1. Презентация Представление чисел в компьютере
- 2. Целые числа в формате с фиксированной запятой max=2n-1 256-1=28-1=255 min=2n-1 max 11111111 1ячейка 8 бит min 00000000
- 3. Целые числа в формате с фиксированной запятойmax=1*27+1*26+1*25+1*24+1*23++1*22+1*21+1*20==1*28-1=255
- 4. Целое число со знаком2 ячейки – 16
- 5. Целое число со знаком-215 = - 2n-1 min -32768215-1 = 2n-1-1 max 327670«+»1« - »
- 6. Длинное целое со знаком4 ячейки
- 7. Достоинства чисел в формате с фиксированной запятой:простота и наглядность представления чиселпростота алгоритмов реализации арифметических операций
- 8. Недостатки чисел в формате с фиксированной запятой:Небольшой
- 9. Дополнительный код для представления целых отрицательных чисел Алгоритм
- 10. Пример получения доп. кода (для числа -2002)
- 11. Пример арифметических действий300010 – 500010=300010 + (-500010)
- 12. Сложим прямой код положительного числа и дополнительный
- 13. Переведем его
- 14. Представление чисел с плавающей запятойА= m *
- 15. Пример арифметических действий 1/n ≤ |m|< 1
- 16. Число в этом формате занимает в памяти
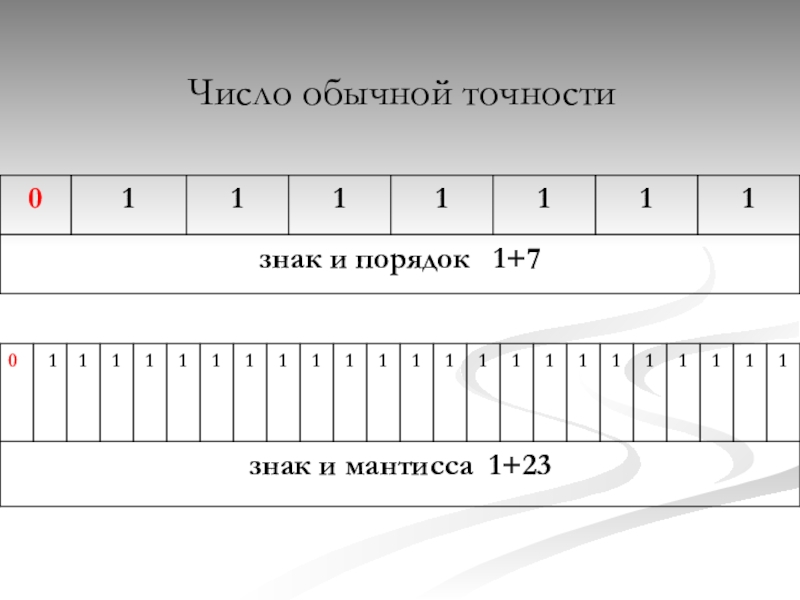
- 17. Число обычной точности
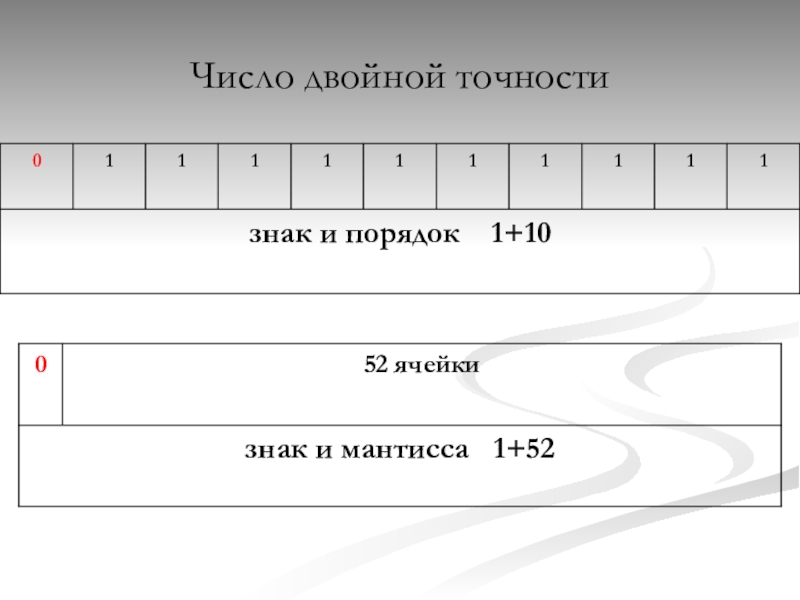
- 18. Число двойной точности
- 19. Список источников информации1. Информатика и информационные технологии.
Целые числа в формате с фиксированной запятой max=2n-1 256-1=28-1=255 min=2n-1 max 11111111 1ячейка 8 бит min 00000000
Слайд 2Целые числа в формате с фиксированной запятой
max=2n-1
256-1=28-1=255
min=2n-1
max 11111111
1ячейка
8 бит
min 00000000
Слайд 3Целые числа в формате с фиксированной запятой
max=1*27+1*26+1*25+1*24+1*23+
+1*22+1*21+1*20==1*28-1=255
Слайд 4Целое число со знаком
2 ячейки – 16 битов
Положительное число формата «знак
- величина» - прямой код числа
2 байта = 16 битов
n=16
2 байта = 16 битов
n=16
Слайд 6Длинное целое со знаком
4 ячейки 4 байта =
32 бита
max 2n-1-1=232-1-1 2 147 483 647
min -2n-1=-232-1 -2 147 483 648
max 2n-1-1=232-1-1 2 147 483 647
min -2n-1=-232-1 -2 147 483 648
Слайд 7Достоинства чисел в формате с фиксированной запятой:
простота и наглядность представления чисел
простота
алгоритмов реализации арифметических операций
Слайд 8Недостатки чисел в формате с фиксированной запятой:
Небольшой диапазон представления величин, недостаточный
для решения математических , физических и других задач, в которых используются как очень малые, так и очень большие числа.
Слайд 9Дополнительный код для представления целых отрицательных чисел
Алгоритм получения дополнительного кода отрицательного
числа:
Модуль числа записать в прямом коде в n двоичных разрядах.
Получить обратный код числа, для этого значения всех битов инвертировать (0 заменить на 1 и наоборот)
К полученному обратному коду прибавить единицу.
Модуль числа записать в прямом коде в n двоичных разрядах.
Получить обратный код числа, для этого значения всех битов инвертировать (0 заменить на 1 и наоборот)
К полученному обратному коду прибавить единицу.
Слайд 12 Сложим прямой код положительного числа и дополнительный код отрицательного числа, получим
результат в дополнительном коде суммы:
+0000101110111000
1110110001111000
1111100000110000
+0000101110111000
1110110001111000
1111100000110000
Слайд 13
Переведем его в десятичное число:
Инвертируем доп.
код суммы: 0000011111001111
Прибавим к полученному коду 1 и получим модуль отрицательного числа:
+0000011111001111
0000000000000001
0000011111010000
3. Переведем в десятичное число и припишем знак отрицательного числа: - 2000
Прибавим к полученному коду 1 и получим модуль отрицательного числа:
+0000011111001111
0000000000000001
0000011111010000
3. Переведем в десятичное число и припишем знак отрицательного числа: - 2000
Слайд 14Представление чисел с плавающей запятой
А= m * qn
Где А –
число, m – мантисса числа, q – основание системы счисления, n – порядок числа.
Слайд 15Пример арифметических действий
1/n ≤ |m|< 1 - нормализованная мантисса
Преобразуем
десятичное число, записанное в естественной форме, в экспоненциальную:
555,5 = 0, 55555 * 103
555,5 = 0, 55555 * 103
Слайд 16Число в этом формате занимает в памяти компьютера 4 (число обычной
точности) или 8 байтов (число двойной точности).
Выделяютя разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы
Выделяютя разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы
Слайд 19Список источников информации
1. Информатика и информационные технологии. Н. Угринович
2. Практикум по
информатике и информационным технологиям. Н. Угринович, Л. Босова, Н. Михайлова