- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Подготовка к ЕГЭ по информатике: проверка истинности логического выражения (задание 18) (10-11 класс)
Содержание
- 1. Презентация Подготовка к ЕГЭ по информатике: проверка истинности логического выражения (задание 18) (10-11 класс)
- 2. ЕГЭ 18 № 295 (задание с сайта
- 3. ЕГЭ 18 № 295 (задание с сайта
- 4. ЕГЭ 18 № 345 (задание с сайта
- 5. ЕГЭ 18 № 340 (задание с сайта
- 6. ЕГЭ 18 № 340 (задание с сайта
- 7. ЕГЭ 18 № 314 (задание с сайта
- 8. ЕГЭ 18 № 314 (задание с сайта
- 9. ЕГЭ 18 № 279 (задание с сайта
Слайд 1Подготовка к ЕГЭ по информатике
Струкова Н.В.
Проверка истинности логического выражения
(ЕГЭ, задание №
Слайд 2ЕГЭ 18 № 295 (задание с сайта Полякова К. Ю.
http://kpolyakov.spb.ru)
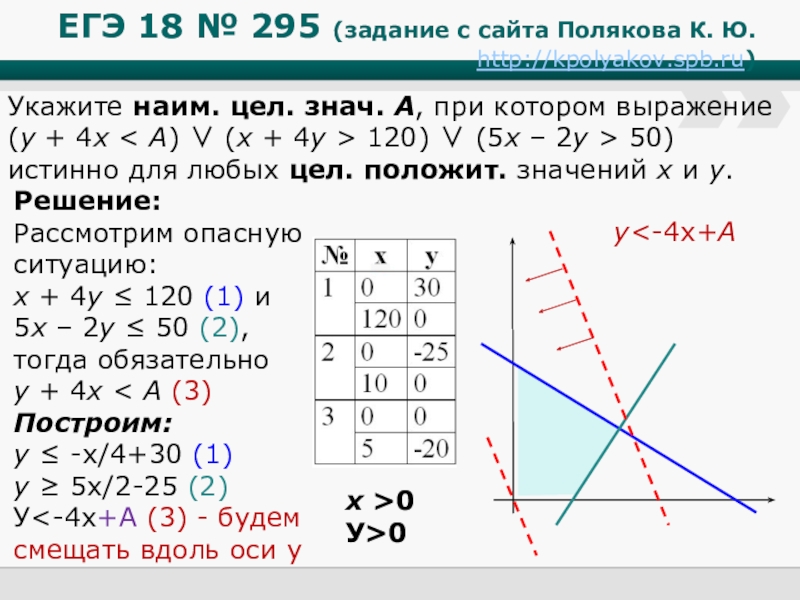
Решение:
Рассмотрим
x + 4y ≤ 120 (1) и
5x – 2y ≤ 50 (2), тогда обязательно
y + 4x < A (3)
Построим:
y ≤ -x/4+30 (1)
y ≥ 5x/2-25 (2)
У<-4х+A (3) - будем смещать вдоль оси у
Укажите наим. цел. знач. А, при котором выражение
(y + 4x < A) ∨ (x + 4y > 120) ∨ (5x – 2y > 50)
истинно для любых цел. положит. значений x и y.
х >0
У>0
y<-4х+A
Слайд 3ЕГЭ 18 № 295 (задание с сайта Полякова К. Ю.
http://kpolyakov.spb.ru)
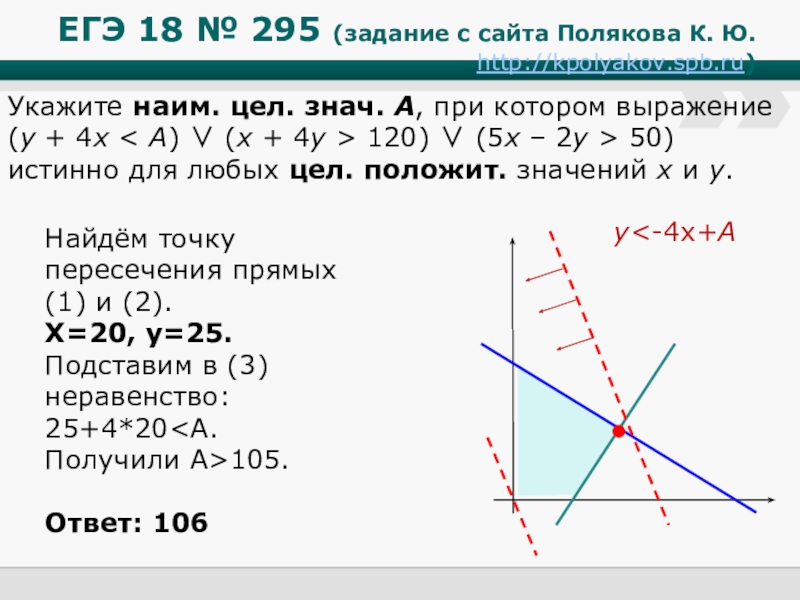
Найдём
Х=20, у=25.
Подставим в (3) неравенство:
25+4*20<А.
Получили А>105.
Ответ: 106
Укажите наим. цел. знач. А, при котором выражение
(y + 4x < A) ∨ (x + 4y > 120) ∨ (5x – 2y > 50)
истинно для любых цел. положит. значений x и y.
y<-4х+A
Слайд 4ЕГЭ 18 № 345 (задание с сайта Полякова К. Ю.
http://kpolyakov.spb.ru)
Укажите
истинно для любых целых неотрицательных значений x и y.
Решение:
Рассмотрим опасную ситуацию:
2x + 3y = 72 (1), тогда обязательно
x < A (2) и у < A (3)
Построим:
2x + 3y = 72 (1)
Х=А (2)
y =А (3)
будем смещать вдоль осей
х ≥0
у≥0
Получили систему:
36<А и 24<А.
Ответ: 37
24
36
Слайд 5ЕГЭ 18 № 340 (задание с сайта Полякова К. Ю.
http://kpolyakov.spb.ru)
Укажите
(2y +5x 17) ∨ (A > 2x + 3y) (A > 4y + x + 1) истинно для любых целых положительных значений x и y.
Решение: х >0
Рассмотрим опасную ситуацию: 2y +5x =17(1), тогда обязательно
A > 2x + 3y (2) и
A > 4y + x + 1 (3)
Построим:
2y +5x =17(1)
У<-2x/3 + А/3 (2)
y
У>0
Слайд 6ЕГЭ 18 № 340 (задание с сайта Полякова К. Ю.
http://kpolyakov.spb.ru)
Укажите
(2y +5x 17) ∨ (A > 2x + 3y) (A > 4y + x + 1) истинно для любых целых положительных значений x и y.
Подставим х=1 в уравнение (1) и найдём у: 2y +5x =17(1),
Х=1, у=6
Подставим в (2) и (3):
A > 2x + 3y (2) и
A > 4y + x + 1 (3)
Получили:
20<А (2) и
26 < А (3)
Ответ: 27
х ≥1
У≥1
Слайд 7ЕГЭ 18 № 314 (задание с сайта Полякова К. Ю.
http://kpolyakov.spb.ru)
Укажите
х ≥1
У≥1
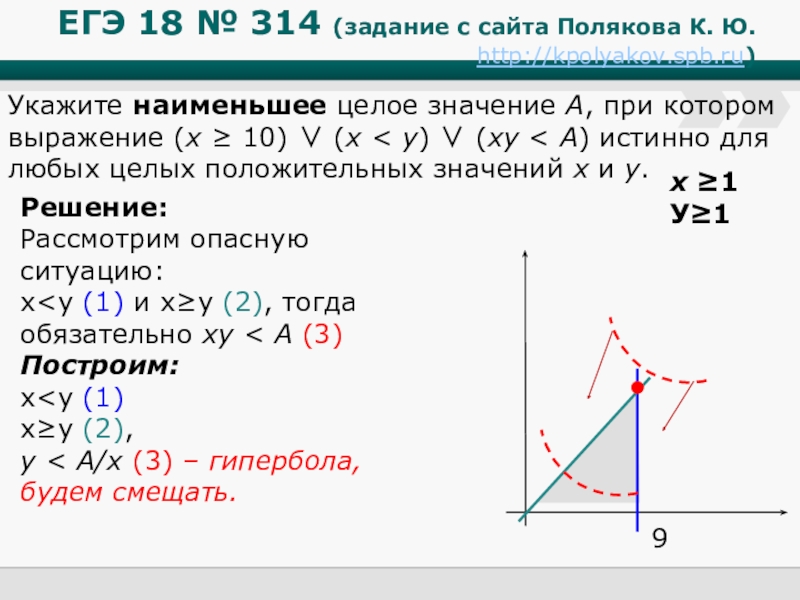
Решение:
Рассмотрим опасную ситуацию:
х<у (1) и х≥у (2), тогда обязательно xy < A (3)
Построим:
х<у (1)
х≥у (2),
y < A/х (3) – гипербола, будем смещать.
9
Слайд 8ЕГЭ 18 № 314 (задание с сайта Полякова К. Ю.
http://kpolyakov.spb.ru)
Укажите
х ≥1
У≥1
9
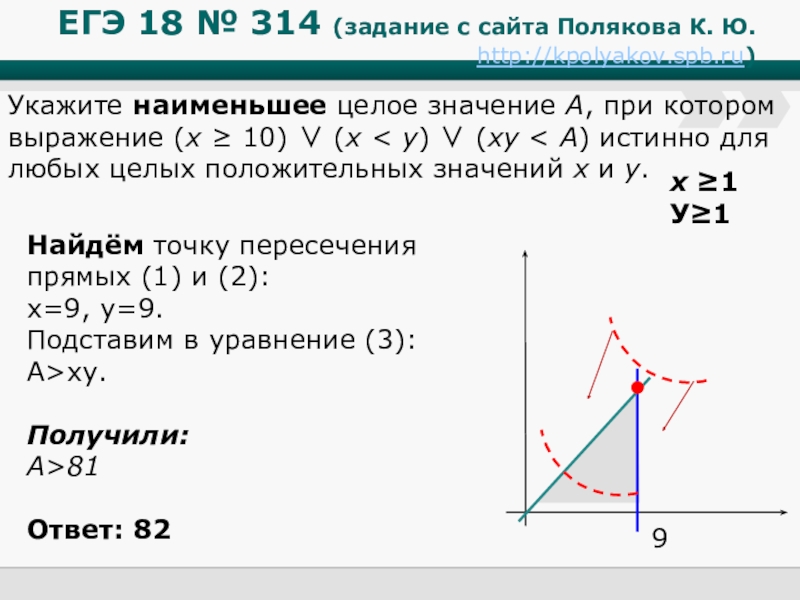
Найдём точку пересечения прямых (1) и (2):
х=9, у=9.
Подставим в уравнение (3):
А>ху.
Получили:
А>81
Ответ: 82
Слайд 9ЕГЭ 18 № 279 (задание с сайта Полякова К. Ю.
http://kpolyakov.spb.ru)
Известно,
( (x A) (x2 64) ) ( (x2 – 48 2x) (x A) )
тождественно истинна (то есть принимает значение 1 при всех вещественных значениях переменной x). Какую наименьшую длину может иметь отрезок A?
Решение: рассмотрим опасные ситуации
(x2 64)=0, тогда x A
2) (x2 – 48 2x)=1, тогда x A
Получили:
1)(x2 > 64),
х (-,-8) (8, ), A [-8, 8]
2) x2 – 48 2x, (х-8)(х+6) 0
х [-6, 8], A [-6, 8]
Наименьшая длина 6+8=14
Ответ: 14
-8
8
-6
8
-
-
+
+
+
+